cs231n assignment2 Batch Normalization

BatchNormalization的反向推导比之前的稍微复杂一些，但是画出计算图后，从后往前推导就会变的简单。

Batch normalization

forward

首先实现layers.py中的batchnorm_forward()函数，实现batch normalization的主要是将数据转换为单位高斯数据，提高模型收敛速度、减少初始化对模型的影响。
归一化公式：
$$x^{(k)}=\frac{x^{(k)}-\mathrm{E}\left[x^{(k)}\right]}{\sqrt{\mathrm{Var}\left[x^{(k)}\right]}}$$

代码：

if mode == 'train':
	# 样本均值和方差
	sample_mean = np.mean(x,axis=0)
    sample_var = np.var(x,axis=0)
    x_hat = (x - sample_mean) / np.sqrt(sample_var + eps)
    out = gamma * x_hat + beta
	

    cache = (x, sample_mean, sample_var, x_hat, eps, gamma, beta)
    running_mean = momentum * running_mean + (1 - momentum) * sample_mean
    running_var = momentum * running_var + (1 - momentum) * sample_var

在测试数据集上使用运行时均值和方差进行计算

elif mode == 'test':
	out = (x - running_mean) * gamma / (np.sqrt(running_var))

backward

首先画出计算图，根据计算图一步一步反向推导导数计算。从图中可以看出dx 和dmean求导时有两处，并且$mean=\frac{{\Sigma }_{X_i}}{N}$，故dx有四处。

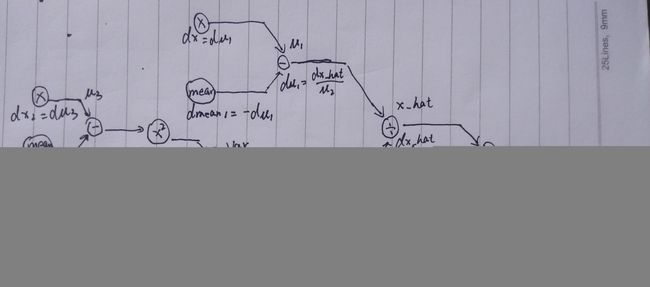
图中大部分导数已经写出来，部分导数写在此处：
$d_{Var}=\frac{1}{2}(var+eps{)}^{-\frac{1}{2}}\cdot d{\mu }_2$
$d{x}_{-}\text{ square }=\frac{1}{N}\cdot d_{\text{ var }}$
$d{\mu }_3=2\cdot (x-\mathrm{mean})\cdot d{x}_{-}\text{ square }$

layers.py中的batchnorm_backward()

# 准备参数
x, mean, var, x_hat, eps, gamma, beta = cache
N = x.shape[0]
mu1 = x - mean
mu2 = np.sqrt(var + eps)

# 反向推导
dbeta = np.sum(dout, axis=0)                                # (D,)
dgamma = np.sum(x_hat * dout, axis=0)                       # (D,)
dx_hat = dout * gamma                                       # (N,D)
dmu1 = dx_hat / mu2                                         # (N,D)
dmu2 = - np.sum(mu1 / mu2 ** 2 * dx_hat, axis=0)            # (D,)
dx1 = dmu1                                                  # (N,D)
dmean1 = -np.sum(dmu1,axis=0)                               # (D,)

dvar = 0.5 * (var + eps) ** (-0.5) * dmu2                   # (D,)
dx_square = 1.0 / N * dvar
dmu3 = 2.0 * (x - mean) * dx_square
dx2 = dmu3
dmean2 = -np.sum(dmu3, axis=0)                              # (D,)

dx3 = 1.0 / N * dmean1
dx4 = 1.0 / N * dmean2

dx = dx1 + dx2 + dx3 + dx4

接下来需要实现一步到位的梯度计算，自己没搞定，参考别人代码。

x, mean, var, x_hat, eps, gamma, beta = cache
N = x.shape[0]
dgamma = np.sum(x_hat * dout, axis=0)
dbeta = np.sum(dout, axis=0)  # (D,)

dx = (1. / N) * gamma * (var + eps) ** (-1. / 2.) * (
                N * dout - np.sum(dout, axis=0) - (x - mean) * (var + eps) ** (-1.0) * np.sum(dout * (x - mean),
                                                                                              axis=0))

Layer Normalization: Implementation

layer norm与batch norm非常相似，都是作用在全连接层。不同的是，batch norn计算均值和标准差时，是在行纬度方向，即axis = 0；layer norm则是在列维度方向上，即axis = 1。

前向传播
layers.py中的layernorm_forward()

sample_mean = np.mean(x, axis=1, keepdims=True)
sample_var = np.var(x, axis=1, keepdims=True)
x_hat = (x - sample_mean) / np.sqrt(sample_var + eps)
out = gamma * x_hat + beta
cache = (x, sample_mean, sample_var, x_hat, eps, gamma, beta

反向传播
layers.py中的layernorm_backward()

(x, mean, var, x_hat, eps, gamma, beta) = cache
N = x.shape[1]
dbeta = np.sum(dout, axis=0)
dgamma = np.sum(dout * x_hat, axis=0)
dx_hat = gamma * dout
dvar = np.sum((x - mean) * dx_hat, axis=1, keepdims=True) * (
                -0.5 / np.sqrt(var + eps) ** 3)

dmean = -1 / np.sqrt(var + eps) * np.sum(dx_hat, axis=1, keepdims=True) + dvar * np.sum(
        -2 * (x - mean), axis=1, keepdims=True) / N

# final gradient
dx = 1 / np.sqrt(var + eps) * dx_hat + 1 / N * dmean + dvar * 2 * (x - mean) / N

---

Inline Question

Inline Question 1
Describe the results of this experiment. How does the scale of weight initialization affect models with/without batch normalization differently, and why?
Answer
权重不同的初始化值对网络有着不同的影响，从图中可以发现当权重范围初始值为接近10^-1时，不论是采用batch normalization或者不采用都有着较高的准确率和较低的损失值。
但是从图中还可以发现，即使在非常坏的初始值情况下，采用batch normalization的网络波动不是很大，也就是说采用batch normalization的网络可以降低坏的初始值影响。

Inline Question 2
Describe the results of this experiment. What does this imply about the relationship between batch normalization and batch size? Why is this relationship observed?
Answer
在一定的范围内，随着batch size的提高，使用batch normalization的网络的准确率也会提高。

Inline Question 3
Which of these data preprocessing steps is analogous to batch normalization, and which is analogous to layer normalization?

1. Scaling each image in the dataset, so that the RGB channels for each row of pixels within an image sums up to 1.
2. Scaling each image in the dataset, so that the RGB channels for all pixels within an image sums up to 1.
3. Subtracting the mean image of the dataset from each image in the dataset.
4. Setting all RGB values to either 0 or 1 depending on a given threshold.

Answer
1、3是batch normalization的步骤
2是layer normalization的步骤
4是dropout

Inline Question 4
When is layer normalization likely to not work well, and why?

1. Using it in a very deep network
2. Having a very small dimension of features
3. Having a high regularization term

Answer
从结果看，layer norm 的效果不是很好，特别是当 batch size 很小时。 但是对深层NN来说，layer norm 可以加快训练速度。 注意，reg只是施加于 weights 上的，并不施加于 norm 的参数 gamma 和 beta。如果 reg 很大的话，那么 affine 层的 weights 会被拉向0，输出值的大小也会减小，因此会减小 norm 层的作用。

参考文章

1. https://blog.csdn.net/weixin_39880579/article/details/86773600
2. https://github.com/ColasGael/cs231n-assignments-spring19/blob/master/assignment2/cs231n/layers.py
3. https://github.com/FortiLeiZhang/cs231n/blob/master/document/Assignment 2 -- BatchNormalization.md