概率论几大分布的期望和方差证明整合
前言
简介
本文是对概率论中常见分布包括二项分布、0-1分布、泊松分布、均匀分布、正态分布、指数分布的期望和方差的证明整合,附加自己的推导或理解。
导览
二项分布 (Binomial Distribution)
泊松分布 (Poisson’s Distribution)
均匀分布 (Uniform Distribution)
正态分布 (Normal Distribution)
指数分布 (Exponential Distribution)
总结
二项分布 (Binomial Distribution) X~B(n,p):E(X)=np,D(X)=np(1-p)=npq 。
0-1分布 X~B(1,p):E(X)=p,D(X)=p(1-p)=pq 。
泊松分布 (Poisson’s Distribution) X~P( λ \lambda λ):E(X)=λ,D(X)=λ 。
均匀分布 (Uniform Distribution) X~U(a,b) :E(X)= ( a + b ) / 2 (a+b)/2 (a+b)/2,D(X)= ( b − a ) 2 / 12 (b-a)^2/12 (b−a)2/12 。
正态分布 (Normal Distribution) X~N(μ,σ):E(X)=μ,D(X)= σ 2 σ^2 σ2。
指数分布 (Exponential Distribution)X~Γ(1,β):E(X)= 1 / λ 1/λ 1/λ,D(X)= 1 / λ 2 1/λ^2 1/λ2 。
正文
二项分布 (Binomial Distribution) From QUETAL and chs007chs
Part Ⅰ From QUETAL
X~B(n,p)
分布律: P ( X = k ) = ( n k ) p k q n − k , k = 0 , 1 , 2 , . . , n , q = 1 − p P(X=k) = {n\choose k}p^kq^{n-k},k = 0,1,2,..,n,q = 1-p P(X=k)=(kn)pkqn−k,k=0,1,2,..,n,q=1−p
期望:
E X = ∑ k = 0 n k ( n k ) p k q n − k = ∑ k = 1 n k ( n k ) p k q n − k = ∑ k = 1 n k n ! k ! ( n − k ) ! p k q n − k = n p ∑ k = 1 n ( n − 1 ) ! ( k − 1 ) ! ( n − k ) ! p k − 1 q ( n − 1 ) − ( k − 1 ) = n p ∑ k = 1 n ( n − 1 k − 1 ) p k − 1 q ( n − 1 ) − ( k − 1 ) = n p [ ( n − 1 0 ) p 0 q n − 1 + ( n − 1 1 ) p 1 q n − 2 + . . . + ( n − 1 n − 1 ) p n − 1 q 0 ] = n p EX = \sum_{k=0}^n k {n\choose k}p^kq^{n-k} \\ = \sum_{k=1}^n k {n\choose k}p^kq^{n-k} \\ = \sum_{k=1}^n k {\frac{n!}{k!(n-k)!}}p^kq^{n-k} \\ = np\sum_{k=1}^n {\frac{(n-1)!}{(k-1)!(n-k)!}}p^{k-1}q^{(n-1)-(k-1)} \\ = np\sum_{k=1}^n{n-1\choose k-1}p^{k-1}q^{(n-1)-(k-1)}\\ = np[{n-1\choose 0}p^0q^{n-1}+{n-1\choose 1}p^1q^{n-2}+...+{n-1\choose n-1}p^{n-1}q^0] \\ = np EX=k=0∑nk(kn)pkqn−k=k=1∑nk(kn)pkqn−k=k=1∑nkk!(n−k)!n!pkqn−k=npk=1∑n(k−1)!(n−k)!(n−1)!pk−1q(n−1)−(k−1)=npk=1∑n(k−1n−1)pk−1q(n−1)−(k−1)=np[(0n−1)p0qn−1+(1n−1)p1qn−2+...+(n−1n−1)pn−1q0]=np
方差: D X = E X 2 − ( E X ) 2 DX = EX^2-(EX)^2 DX=EX2−(EX)2
计算EX^2:
E X 2 = ∑ k = 1 n k 2 ( n k ) p k q n − k , k = 0 , 1 , 2 , . . , n , q = 1 − p = ∑ k = 1 n [ k ( k − 1 ) + k ] ( n k ) p k q n − k = ∑ k = 1 n k ( k − 1 ) ( n k ) p k q n − k + ∑ k = 1 n k ( n k ) p k q n − k 其 中 , ∑ k = 1 n k ( n k ) p k q n − k = E X = n p ∑ k = 1 n k ( k − 1 ) ( n k ) p k q n − k = ∑ k = 1 n k ( k − 1 ) n ! k ! ( n − k ) ! p 2 p k − 2 q n − k = ∑ k = 2 n k ( k − 1 ) n ! k ! ( n − k ) ! p 2 p k − 2 q n − k EX^2 = \sum_{k=1}^nk^2{n\choose k}p^kq^{n-k}, k = 0,1,2,..,n,q = 1-p\\ = \sum_{k=1}^n[k(k-1)+k]{n\choose k}p^kq^{n-k}\\ = \sum_{k=1}^nk(k-1){n\choose k}p^kq^{n-k} + \sum_{k=1}^nk{n\choose k}p^kq^{n-k}\\ 其中, \sum_{k=1}^nk{n\choose k}p^kq^{n-k} = EX = np\\ \sum_{k=1}^nk(k-1){n\choose k}p^kq^{n-k} \\ = \sum_{k=1}^nk(k-1){\frac{n!}{k!(n-k)!}}p^2p^{k-2}q^{n-k} \\ = \sum_{k=2}^nk(k-1){\frac{n!}{k!(n-k)!}}p^2p^{k-2}q^{n-k} \\ EX2=k=1∑nk2(kn)pkqn−k,k=0,1,2,..,n,q=1−p=k=1∑n[k(k−1)+k](kn)pkqn−k=k=1∑nk(k−1)(kn)pkqn−k+k=1∑nk(kn)pkqn−k其中,k=1∑nk(kn)pkqn−k=EX=npk=1∑nk(k−1)(kn)pkqn−k=k=1∑nk(k−1)k!(n−k)!n!p2pk−2qn−k=k=2∑nk(k−1)k!(n−k)!n!p2pk−2qn−k注:特别注意这里k=1时项为0,所以可以从k=2开始计算。 = ∑ k = 1 n n ( n − 1 ) ( n − 2 ) ! ( k − 2 ) ! ( n − k ) ! p 2 p k − 2 q [ ( n − 2 ) − ( k − 2 ) ] = n ( n − 1 ) p 2 ∑ k = 2 n ( n − 2 ) ! ( k − 2 ) ! ( n − k ) ! p k − 2 q [ ( n − 2 ) − ( k − 2 ) ] = n ( n − 1 ) p 2 ∑ k = 2 n ( n − 2 k − 2 ) p k − 2 q [ ( n − 2 ) − ( k − 2 ) ] = n ( n − 1 ) p 2 → E X 2 = n ( n − 1 ) p 2 + n p \\ = \sum_{k=1}^n{\frac{n(n-1)(n-2)!}{(k-2)!(n-k)!}}p^2p^{k-2}q^{[(n-2)-(k-2)]} \\ = n(n-1)p^2\sum_{k=2}^n{\frac{(n-2)!}{(k-2)!(n-k)!}}p^{k-2}q^{[(n-2)-(k-2)]}\\ = n(n-1)p^2\sum_{k=2}^n{n-2\choose k-2}p^{k-2}q^{[(n-2)-(k-2)]}\\ = n(n-1)p^2 \\ \rightarrow EX^2 = n(n-1)p^2+np \\ =k=1∑n(k−2)!(n−k)!n(n−1)(n−2)!p2pk−2q[(n−2)−(k−2)]=n(n−1)p2k=2∑n(k−2)!(n−k)!(n−2)!pk−2q[(n−2)−(k−2)]=n(n−1)p2k=2∑n(k−2n−2)pk−2q[(n−2)−(k−2)]=n(n−1)p2→EX2=n(n−1)p2+np → D X = E X 2 − ( E X ) 2 = n p − n p 2 = n p ( 1 − p ) \rightarrow DX = EX^2-(EX)^2 = np-np^2 = np(1-p) →DX=EX2−(EX)2=np−np2=np(1−p)
Part Ⅱ 0-1分布 From chs007chs
X~B(1,p)
泊松分布 (Poisson’s Distribution) From saltriver
X~P( λ \lambda λ)
分布律: P ( X = k ) = λ k e − λ k ! P(X=k)=\frac{\lambda ^{k}e^{-\lambda }}{k!} P(X=k)=k!λke−λ
期望:
E ( X ) = ∑ k = 0 ∞ k ⋅ λ k e − λ k ! E(X)=\sum_{k=0}^{\infty }k\cdot \frac{\lambda ^{k}e^{-\lambda }}{k!} \\ E(X)=k=0∑∞k⋅k!λke−λ 因 为 k = 0 时 , k ⋅ λ k e − λ k ! = 0 因为k=0时, k⋅λke−λk!=0 \\ 因为k=0时,k⋅λke−λk!=0 E ( X ) = ∑ k = 1 ∞ k ⋅ λ k e − λ k ! E(X)=\sum_{k=1}^{\infty }k\cdot \frac{\lambda ^{k}e^{-\lambda }}{k!} \\ E(X)=k=1∑∞k⋅k!λke−λ E ( X ) = ∑ k = 1 ∞ k ⋅ λ k e − λ k ! = ∑ k = 1 ∞ λ k e − λ ( k − 1 ) ! = ∑ k = 1 ∞ λ k − 1 λ e − λ ( k − 1 ) ! = λ e − λ ∑ k = 1 ∞ λ k − 1 ( k − 1 ) ! E(X)=\sum_{k=1}^{\infty }k\cdot \frac{\lambda ^{k}e^{-\lambda }}{k!}=\sum_{k=1}^{\infty } \frac{\lambda ^{k}e^{-\lambda }}{(k-1)!}=\sum_{k=1}^{\infty } \frac{\lambda ^{k-1}\lambda e^{-\lambda }}{(k-1)!}=\lambda e^{-\lambda }\sum_{k=1}^{\infty } \frac{\lambda ^{k-1}}{(k-1)!} \\ E(X)=k=1∑∞k⋅k!λke−λ=k=1∑∞(k−1)!λke−λ=k=1∑∞(k−1)!λk−1λe−λ=λe−λk=1∑∞(k−1)!λk−1 用 到 泰 勒 展 开 式 : e x = 1 + x + x 2 2 ! + x 3 3 ! + . . . + x n n ! + . . . = ∑ k = 1 ∞ x k − 1 ( k − 1 ) ! 用到泰勒展开式:e^{x}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+...+\frac{x^{n}}{n!}+...=\sum_{k=1}^{\infty } \frac{x ^{k-1}}{(k-1)!} \\ 用到泰勒展开式:ex=1+x+2!x2+3!x3+...+n!xn+...=k=1∑∞(k−1)!xk−1 E ( X ) = λ e − λ ∑ k = 1 ∞ λ k − 1 ( k − 1 ) ! = λ e − λ e λ = λ E(X)=\lambda e^{-\lambda }\sum_{k=1}^{\infty } \frac{\lambda ^{k-1}}{(k-1)!}=\lambda e^{-\lambda }e^{\lambda }=\lambda E(X)=λe−λk=1∑∞(k−1)!λk−1=λe−λeλ=λ
方差: D X = E X 2 − ( E X ) 2 DX = EX^2-(EX)^2 DX=EX2−(EX)2
计算EX^2:
E ( X 2 ) = ∑ k = 0 ∞ k 2 ⋅ λ k e − λ k ! = λ e − λ ∑ k = 1 ∞ k λ k − 1 ( k − 1 ) ! = λ e − λ ∑ k = 1 ∞ ( k − 1 + 1 ) λ k − 1 ( k − 1 ) ! E(X^2)=\sum_{k=0}^{\infty }k^2 \cdot \frac{\lambda ^{k}e^{-\lambda }}{k!}=\lambda e^{-\lambda} \sum_{k=1}^{\infty } \frac{k \lambda ^{k-1}}{(k-1)!}=\lambda e^{-\lambda} \sum_{k=1}^{\infty } \frac{(k-1+1) \lambda ^{k-1}}{(k-1)!} \\ E(X2)=k=0∑∞k2⋅k!λke−λ=λe−λk=1∑∞(k−1)!kλk−1=λe−λk=1∑∞(k−1)!(k−1+1)λk−1 = λ e − λ ( ∑ m = 0 ∞ m ⋅ λ m m ! + ∑ m = 0 ∞ λ m m ! ) ( m = k − 1 ) =\lambda e^{-\lambda} (\sum_{m=0}^{\infty } \frac{m \cdot \lambda ^{m}}{m!}+\sum_{m=0}^{\infty } \frac{ \lambda ^{m}}{m!}) (m=k-1) \\ =λe−λ(m=0∑∞m!m⋅λm+m=0∑∞m!λm)(m=k−1) = λ e − λ ( λ ⋅ ∑ m = 1 ∞ λ m − 1 ( m − 1 ) ! + ∑ m = 0 ∞ λ m m ! ) =\lambda e^{-\lambda} ( \lambda \cdot \sum_{m=1}^{\infty } \frac{\lambda ^{m-1}}{(m-1)!}+\sum_{m=0}^{\infty } \frac{ \lambda ^{m}}{m!}) \\ =λe−λ(λ⋅m=1∑∞(m−1)!λm−1+m=0∑∞m!λm) = λ e − λ ( λ e λ + e λ ) = λ ( λ + 1 ) =\lambda e^{-\lambda}(\lambda e^{\lambda}+e^\lambda)=\lambda(\lambda+1) \\ =λe−λ(λeλ+eλ)=λ(λ+1) → D ( X ) = E ( X 2 ) − ( E ( X ) ) 2 = λ ( λ + 1 ) − λ 2 = λ \rightarrow D(X)=E(X^2)-(E(X))^2=\lambda(\lambda+1)-\lambda^2=\lambda →D(X)=E(X2)−(E(X))2=λ(λ+1)−λ2=λ
均匀分布 (Uniform Distribution) From chs007chs
X~U(a,b)
正态分布 (Normal Distribution) From 一只驽马
X~N(μ,σ)
概率密度函数: f X ( x ) = 1 σ 2 π exp { − ( x − μ ) 2 2 σ 2 } f_X(x) =\frac{1}{\sigma\sqrt{2\pi}}\exp\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\} fX(x)=σ2π1exp{−2σ2(x−μ)2}
期望: E ( x ) = μ ∫ − ∞ + ∞ N ( x ∣ μ ′ = 0 , σ 2 ) d x = μ E(x) = \mu\int_{-\infty}^{+\infty}\mathcal{N}(x|\mu' = 0, \sigma^2)dx = \mu E(x)=μ∫−∞+∞N(x∣μ′=0,σ2)dx=μ
方差: ⇒ V ( X ) = σ 2 4 π 1 2 π 2 = σ 2 \Rightarrow V(X) = \sigma^2\frac{4}{\sqrt{\pi}}\frac 12 \frac {\sqrt \pi}{2} = \sigma^2 ⇒V(X)=σ2π4212π=σ2
指数分布 (Exponential Distribution) From saltriver
X~Γ(1,β)
概率密度函数: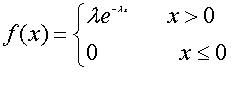
期望:
E ( X ) = ∫ − ∞ ∞ ∣ x ∣ f ( x ) d x = ∫ 0 ∞ x f ( x ) d x = ∫ 0 ∞ x ⋅ λ e − λ x d x = 1 λ ∫ 0 ∞ λ x e − λ x d λ x 令 u = λ x , E ( X ) = 1 λ ∫ 0 ∞ u e − u d u = 1 λ [ ( − e − u − u e − u ) ∣ ( ∞ , 0 ) ] = 1 λ E(X)=\int_{-\infty }^{\infty }|x|f(x)dx=\int_{0}^{\infty }xf(x)dx=\int_{0}^{\infty }x\cdot\lambda e^{-\lambda x}dx=\frac {1} {\lambda}\int_{0}^{\infty }\lambda xe^{-\lambda x}d\lambda x \\ 令u=λx,E(X)=\frac {1} {\lambda}\int_{0}^{\infty }ue^{-u}du=\frac {1} {\lambda}[(-e^{-u}-ue^{-u})|(\infty,0)]=\frac {1} {\lambda} \\ E(X)=∫−∞∞∣x∣f(x)dx=∫0∞xf(x)dx=∫0∞x⋅λe−λxdx=λ1∫0∞λxe−λxdλx令u=λx,E(X)=λ1∫0∞ue−udu=λ1[(−e−u−ue−u)∣(∞,0)]=λ1
方差: D X = E X 2 − ( E X ) 2 DX = EX^2-(EX)^2 DX=EX2−(EX)2
计算EX^2:
E ( X 2 ) = ∫ − ∞ ∞ ∣ x 2 ∣ f ( x ) d x = ∫ 0 ∞ x 2 f ( x ) d x = ∫ 0 ∞ x 2 ⋅ λ e − λ x d x E ( X 2 ) = 1 λ 2 ∫ 0 ∞ λ x λ x e − λ x d λ x 令 u = λ x , E ( X 2 ) = 1 λ 2 ∫ 0 ∞ u 2 e − u d u = 1 λ 2 [ ( − 2 e − u − 2 u e − u − u 2 e − u ) ∣ ( ∞ , 0 ) ] = 1 λ 2 ⋅ 2 = 2 λ 2 → D ( X ) = E ( X 2 ) − ( E ( X ) ) 2 = 2 λ 2 − ( 1 λ ) 2 = 1 λ 2 E(X^2)=\int_{-\infty }^{\infty }|x^2|f(x)dx=\int_{0}^{\infty }x^2f(x)dx=\int_{0}^{\infty }x^2\cdot\lambda e^{-\lambda x}dx \\ E(X^2)=\frac {1} {\lambda^2}\int_{0}^{\infty }\lambda x \lambda xe^{-\lambda x}d\lambda x \\ 令u=λx,E(X^2)=\frac {1} {\lambda^2}\int_{0}^{\infty }u^2e^{-u}du=\frac {1} {\lambda^2}[(-2e^{-u}-2ue^{-u}-u^2e^{-u})|(\infty,0)]=\frac {1} {\lambda^2}\cdot 2=\frac {2} {\lambda^2} \\ \rightarrow D(X)=E(X^2)-(E(X))^2=\frac {2} {\lambda^2}-(\frac {1} {\lambda})^2=\frac {1} {\lambda^2} E(X2)=∫−∞∞∣x2∣f(x)dx=∫0∞x2f(x)dx=∫0∞x2⋅λe−λxdxE(X2)=λ21∫0∞λxλxe−λxdλx令u=λx,E(X2)=λ21∫0∞u2e−udu=λ21[(−2e−u−2ue−u−u2e−u)∣(∞,0)]=λ21⋅2=λ22→D(X)=E(X2)−(E(X))2=λ22−(λ1)2=λ21

