形式语言与自动机_笔记整理(二)_上下文无关文法与下推自动机

Context-Free Grammars

CFG Formalism

Terminals = symbols of the alphabet of the language being defined.

Variables = Nonterminals = a finite set of other symbols, each of which represents a language.

Start Symbol = the variable whose language is the one being defined.

Production
variable(head)->string of variables and terminals(body)

Iterated Derivation
=>* means "zero or more derivation steps."

Sentential Form
Any string of variables and/or terminals derived from the start symbol.
Formally, α is a sentential form iff S=>∗ α .

Context-Free Language
If G is a CFG, then the language of G, i.e., L(G) is {w|S=>∗w} .
A language that is defined by some CFG is called a context-free language.

BNF Notation

• Variables are words in <…>;
• Terminals are often multicharacter strings indicated by boldface or underline;
• Symbol ::= is often used for ->.
• Symbol | is used for "or."
• Symbol … is used for "one or more."
• Surround one or more symbols by […] to make them optional.
• Use {…} to surround a sequence of symbols that need to be treated as a unit.

Leftmost and Rightmost Derivations

Derivations allow us to replace any of the variables in a string.
Leads to many different derivations of the same string.
By forcing the leftmost variable (or alternatively, the rightmost variable) to be replaced, we avoid these "distinctions without a difference".

Leftmost Derivations

Say wAα=>lmwβα if w is a string of terminals only and A→β is a production.
Also, α=>∗lmβ if α becomes β by a sequence of 0 or more =>lm steps.

Rightmost Derivations

Say αAw=>rmαβ w if w is a string of terminals only and A→β is a production.
Also, α=>∗rmβ if α becomes β by a sequence of 0 or more =>rm steps.

Parse Trees

• Parse trees are trees labeled by symbols of a particular CFG.
• Leaves: labeled by a terminal or ε.
• Interior nodes: labeled by a variable.
• Children are labeled by the body of a production for the parent.
• Root: must be labeled by the start symbol.

Yield of a Parse Tree

The concatenation of the labels of the leaves in left-to-right order (that is, in the order of a preorder traversal) is called the yield of the parse tree.

Generalization of Parse Trees

We sometimes talk about trees that are not exactly parse trees, but only because the root is labeled by some variable A that is not the start symbol.
Call these parse trees with root A.

Trees, leftmost, and rightmost derivations correspond

• If there is a parse tree with root labeled A and yield w, then A=>∗lm w.
• If A =>∗lm w, then there is a parse tree with root A and yield w.

Ambiguous Grammar

• A CFG is ambiguous if there is a string in the language that is the yield of two or more parse trees.

• Equivalent definitions of "ambiguous grammar"

  • There is a string in the language that has two different leftmost derivations.
  • There is a string in the language that has two different rightmost derivations.

• Ambiguity is a Property of Grammars, not Languages.

  For the balanced-parentheses language, here is another CFG, which is unambiguous.

LL(1) Grammars

• As an aside, a grammar where you can always figure out the production to use in a leftmost derivation by scanning the given string left-to-right and looking only at the next one symbol is called LL(1).
  
  • Leftmost derivation, left-to-right scan, one symbol of lookahead.
• Most programming languages have LL(1) grammars.
  
  • LL(1) grammars are never ambiguous.

Inherent Ambiguity

• Certain CFL' s are inherently ambiguous, meaning that every grammar for the language is ambiguous.
• Every grammar for the language is ambiguous.

Normal Forms for CFG’ s

Eliminating Useless Symbols

• A symbol is useful if it appears in some derivation of some terminal string from the start symbol.

• Otherwise, it is useless.

• Eliminate symbols that derive no terminal string.
• Eliminate unreachable symbols.

Eliminate Variables That Derive Nothing

• Discover all variables that derive terminal strings.
• For all other variables, remove all productions in which they appear in either the head or body.

S -> AB | C, A -> aA | a, B -> bB, C -> c
Basis: A and C are discovered because of A -> a and C -> c.
Induction: S is discovered because of S -> C.
Nothing else can be discovered.
Result: S -> C, A -> aA | a, C -> c

Eliminate unreachable symbols

• Remove from the grammar all symbols not discovered reachable from S and all productions that involve these symbols.

Eliminate ε-Productions

Epsilon Productions

Theorem: If L is a CFL, then L-{ε} has a CFG with no ε-productions.
Note: ε cannot be in the language of any grammar that has no ε–productions.

Nullable Symbols

nullable symbols = variables A such that A =>* ε.

S -> AB, A -> aA | ε, B -> bB | A

Basis: A is nullable because of A -> ε.
Induction: B is nullable because of B -> A.
Then, S is nullable because of S -> AB.

Key idea: turn each production A→X1…Xn into a family of productions.
For each subset of nullable X' s, there is one production with those eliminated from the right side "in advance".

• Except, if all X' s are nullable (or the body was empty to begin with), do not make a production with ε as the right side.

Eliminate Unit Productions

Unit Productions

• A unit production is one whose body consists of exactly one variable.
• These productions can be eliminated.
• Key idea: If A=>∗B by a series of unit productions, and B→α is a non-unit-production, then add production A→α .
• Then, drop all unit productions.
  

• Find all pairs (A, B) such that A =>* B by a sequence of unit productions only.

Cleaning Up a Grammar

Theorem: if L is a CFL, then there is a CFG for L – {ε} that has:

• No useless symbols.
• No ε-productions.
• No unit productions.

i.e., every body is either a single terminal or has length > 2.

Perform the following steps in order:

• Eliminate ε-productions.
• Eliminate unit productions.
• Eliminate variables that derive no terminal string.
• Eliminate variables not reached from the start symbol.

Chomsky Normal Form

A CFG is said to be in Chomsky Normal Form if every production is of one of these two forms:

• A -> BC (body is two variables).
• A -> a (body is a single terminal).

Theorem: If L is a CFL, then L – {ε} has a CFG in CNF.

Step 1: Clean the grammar, so every body is either a single terminal or of length at least 2.
Step 2: For each body ≠a single terminal, make the right side all variables.

• For each terminal a create new variable Aa and production Aa→a .
• Replace a by Aa in bodies of length > 2.

Consider production A→BcDe `.
We need variables Ac and Ae with productions Ac→c and Ae→e .

• Note: you create at most one variable for each terminal, and use it everywhere it is needed.

Replace A→BcDe by A→BAcDAe .

Step 3: Break right sides longer than 2 into a chain of productions with right sides of two variables.

Example: A -> BCDE is replaced by A -> BF, F -> CG, and G -> DE.

• F and G must be used nowhere else.

Recall A -> BCDE is replaced by A -> BF, F -> CG, and G -> DE.
In the new grammar, A => BF => BCG => BCDE.

More importantly: Once we choose to replace A by BF, we must continue to BCG and BCDE.

• Because F and G have only one production.

Pushdown Automata

• The PDA is an automaton equivalent to the CFG in language-defining power.
• Only the nondeterministic PDA defines all the CFL' s.
• But the deterministic version models parsers.
  
  • Most programming languages have deterministic PDA' s.

PDA Formalism

A PDA is described by:

• A finite set of states (Q, typically).
• An input alphabet (Σ, typically).
• A stack alphabet (Γ, typically).
• A transition function (δ, typically).
  
  • Takes three arguments:
    
    • A state, in Q.
    • An input, which is either a symbol in Σ or ε .
    • A stack symbol in Γ.
  • δ(q, a, Z) is a set of zero or more actions of the form ( p , α ).
    
    • p is a state.
    • α is a string of stack symbols.
• A start state ( q0 , in Q, typically).
• A start symbol ( Z0 , in Γ, typically).
• A set of final states ( F⊆Q , typically).

Actions of the PDA

If δ(q, a, Z) contains (p, α ) among its actions, then one thing the PDA can do in state q, with a at the front of the input, and Z on top of the stack is:
1. Change the state to p.
2. Remove a from the front of the input (but a may be ε).
3. Replace Z on the top of the stack by α .

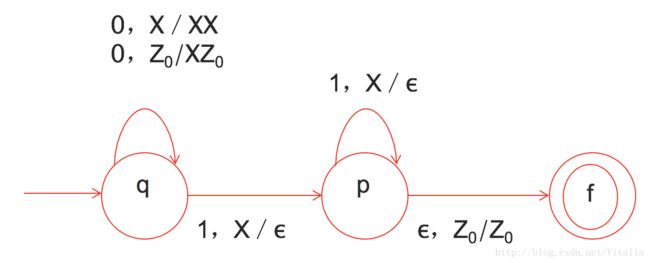
Example: DFA

Design a PDA to accept { 0n1n | n > 1}.
The states:

• q = start state. We are in state q if we have seen only 0' s so far.
• p = we' ve seen at least one 1 and may now proceed only if the inputs are 1' s.
• f = final state; accept.

The stack symbols:

• Z0 = start symbol. Also marks the bottom of the stack, so we know when we have counted the same number of 1's as 0' s.
• X = marker, used to count the number of 0' s seen on the input.

The transitions:

• δ( q,0,Z0 ) = {( q,XZ0 )}.
• δ(q, 0, X) = {(q, XX)}.
  
  • These two rules cause one X to be pushed onto the stack for each 0 read from the input.
• δ(q, 1, X) = {(p, ε)}. When we see a 1, go to state p and pop one X.
• δ(p, 1, X) = {(p, ε)}. Pop one X per 1.
• δ( p,ε,Z0 ) = {( f,Z0 )}. Accept at bottom.

Actions of the Example PDA

Graphical Presentation

Instantaneous Descriptions

We can formalize the pictures just seen with an instantaneous description(ID).
A ID is a triple (q, w, α ), where:

• q is the current state.
• w is the remaining input.
• α is the stack contents, top at the left.

The "Goes-To" Relation

To say that ID I can become ID J in one move of the PDA, we write I⊦J .
Formally, (q,aw,Xα)⊦(p,w,βα) for any w and α , if δ(q,a,X) contains (p,β) .
Extend ⊦ to ⊦*, meaning "zero or more moves".

Using the previous example PDA, we can describe the sequence of moves by:
(q,000111,Z0)⊦(q,00111,XZ0)⊦(q,0111,XXZ0)⊦(q,111,XXXZ0)⊦(p,11,
XXZ0)⊦(p,1,XZ0)⊦(p,ε,Z0)⊦(f,ε,Z0).
Thus, (q,000111,Z0)⊦*(f,ε,Z0).

Theorem 1: Given a PDA P, if (q,x,α)⊦∗(p,y,β) , for all the string w in Σ∗ and all the string γ in Γ∗ , we have (q,xw,αγ)⊦∗(p,yw,βγ)
Theorem 2: Given a PDA P, if (q,xw,α)⊦∗(p,yw,β) , we have (q,x,α)⊦∗(p,y,β)

Language of a PDA

• The common way to define the language of a PDA is by final state.

  If P is a PDA, then L(P) is the set of strings w such that (q0,w,Z0)⊦∗(f,ε,α) for final state f and any α .

• Another language defined by the same PDA is by empty stack.

  If P is a PDA, then N(P) is the set of strings w such that (q0,w,Z0)⊦∗(q,ε,ε) for any state q.

Equivalence of Language Definitions

• If L = L(P), then there is another PDA P' such that L = N(P').
• If L = N(P), then there is another PDA P'' such that L = L(P'').

Deterministic PDA' s

• To be deterministic, there must be at most one choice of move for any state q, input symbol a, and stack symbol X.
• In addition, there must not be a choice between using input ε or real input.
  
  • Formally, δ(q, a, X) and δ(q, ε, X) cannot both be nonempty.

NPDA v.s. DPDA

• NPDA is more powerful than DPDA.

• Think about wwR .

• Theorem:
  If L is a regular language, there exists a DPDA P, such that L=L(P).
  Think about a DFA with a stack that never change…
  Note: It's NOT true of empty stack. Take {0}* for example.

  RE=>DPDA(L(P))=>NPDA
  RE ≠ >DPDA(N(p))=>DPDA(L(P))

DPDA and Ambiguity

• Given a DPDA P defined by final states, L=L(P), L has a non-ambiguous grammar.
• However, non-ambiguous grammars don't have to be able to be presented by DPDA.

Equivalence of PDA, CFG

CFG' s and PDA' s are both useful to deal with properties of the CFL' s.
Also, PDA's, being "algorithmic", are often easier to use when arguing that a language is a CFL.

• Example: It is easy to see how a PDA can recognize balanced parentheses; not so easy as a grammar.

Converting a CFG to a PDA

Let L=L(G) .
Construct PDA P such that N(P)=L .
P has:

• One state q .
• Input symbols = terminals of G .
• Stack symbols = all symbols of G .
• Start symbol = start symbol of G .

At each step, P represents some left-sentential form (step of a leftmost derivation).
If the stack of P is α , and P has so far consumed x from its input, then P represents left-sentential form xα .
At empty stack, the input consumed is a string in L(G) .

Transition Function of P

1. δ(q, a, a) = (q, ε). (Type 1 rules)
   This step does not change the LSF represented, but "moves" responsibility for a from the stack to the consumed input.

2. If A→α is a production of G, then δ(q,ε,A) contains (q,α) . (Type 2 rules)

From a PDA to a CFG

Now, assume L=N(P) .
We' ll construct a CFG G such that L=L(G) .

Intuition

G will have variables [pXq] generating exactly the inputs that cause P to have the net effect of popping stack symbol X while going from state p to state q.

Variables of G

G' s variables are of the form [pXq].
This variable generates all and only the strings w such that (p,w,X)⊦∗(q,ε,ε) .
Also a start symbol S we' ll talk about later.

Productions of G

Each production for [pXq] comes from a move of P in state p with stack symbol X.

• Simplest case:
  δ(p, a, X) contains (q, ε).
  Note a can be an input symbol or ε.
  Then the production is [pXq]->a.
  Here, [pXq] generates a, because reading a is one way to pop X and go from p to q.

• Next simplest case:
  δ(p, a, X) contains (r, Y) for some state r and symbol Y.
  G has production [pXq]->a[rYq].
  We can erase X and go from p to q by reading a (entering state r and replacing the X by Y) and then reading some w that gets P from r to q while erasing the Y.

• Third simplest case:
  δ(p, a, X) contains (r, YZ) for some state r and symbols Y and Z.
  Now, P has replaced X by YZ.
  To have the net effect of erasing X, P must erase Y, going from state r to some state s, and then erase Z, going from s to q.
  Since we do not know state s, we must generate a family of productions:[pXq]->a[rYs][sZq] for all states s.
  [pXq]=>*auv whenever [rYs]=>*u and [sZq]=>*v.

• General Case:
  Suppose δ(p,a,X) contains (r,Y1,…,Yk) for some state r and k > 3.
  Generate family of productions:
  [pXq]→a[rY1s1][s1Y2s2]…[sk−2Yk−1sk−1][sk−1Ykq] .

We can prove that (q0,w,Z0)⊦∗(p,ε,ε) iff [q0Z0p]=>∗w .

Add to G another variable , the start symbol S, and add productions S→[q0Z0p] for each state p.

The Pumping Lemma for CFL's

We can always find two pieces of any sufficiently long string to "pump" in tandem.
That is: if we repeat each of the two pieces the same number of times, we get another string in the language.

Statement of the CFL Pumping Lemma

For every context-free language L, there is an integer n, such that
For every string z in L of length ≥ n, there exists z = uvwxy such that:

• |vwx| ≤ n.
• |vx| > 0.
• For all i > 0, uviwxiy is in L.

Using the Pumping Lemma

{0i10i|i≥1} is a CFL.

• We can match one pair of counts.

But L = {0i10i10i|i>1} is not.

• We can't match two pairs, or three counts as a group.

• Proof (using the pumping lemma)
  Suppose L were a CFL.
  Let n be L's pumping-lemma constant.
  Consider z=0n10n10n .
  We can write z = uvwxy, where |vwx| ≤ n, and |vx| ≥ 1.

  Case 1: vx has no 0's.
  Then at least one of them is a 1, and uwy has at most one 1, which no string in L does.

  Case 2: vx has at least one 0.

  • vwx is too short (length ≤ n) to extend to all three blocks of 0's in 0n10n10n .
  • Thus, uwy has at least one block of n 0's, and at least one block with fewer than n 0's.
  • Thus, uwy is not in L.

Properties of Context-Free Languages

Many questions that can be decided for regular sets cannot be decided for CFL's.

Decision Properties of Context-Free Languages

Testing Emptiness

If the start symbol is one of useless variables, then the CFL is empty; otherwise not.

Testing Membership

Assume G is in CNF or Convert the given grammar to CNF.
Note: w = ε is a special case, solved by testing if the start symbol is nullable.

Algorithm CYK

Algorithm CYK is a good example of dynamic programming and runs in time O(n3) , where n = |w|.

Let w = a1…an .
We construct an n-by-n triangular array of sets of variables.
Xij = {variables A | A =>* ai⋯aj }.
Induction on j–I+1 (length of the derived string)
Finally, ask if S is in X1n .

Testing Infiniteness

(Note: The idea is essentially the same as for regular languages.)
Use the pumping lemma constant n.
If there is a string in the language of length between n and 2n−1 , then the language is infinite; otherwise not.

Closure Properties of CFL's

CFL' s are closed under union, concatenation, and Kleene closure.
Also, under reversal, homomorphisms and inverse homomorphisms.
But NOT under intersection or difference.

Closure of CFL's Under Union

Proof:

• Let L and M be CFL' s with grammars G and H , respectively.
  Assume G and H have no variables in common.
  Then, add a new start symbol S .
  Add productions S→S1|S2 .
  In the new grammar, all derivations start with S.
  The first step replaces S by either S1 or S2 . In the first case, the result must be a string in L(G)=L , and in the second case a string in L(H)=M .

Closure of CFL's Under Concatenation

Proof:

• Let L and M be CFL's with grammars G and H , respectively.
  Let S1 and S2 be the start symbols of G and H .
  Form a new grammar for LM by starting with all symbols and productions of G and H .
  Add a new start symbol S .
  Add production S→S1S2 .
  Every derivation from S results in a string in L followed by one in M .

Closure of CFL's Under Star

Proof:

• Let L have grammar G , with start symbol S1 .
  Form a new grammar for L∗ by introducing to G a new start symbol S and the productions S→S1S | ε.
  A rightmost derivation from S generates a sequence of zero or more S1 's, each of which generates some string in L .

Closure of CFL's Under Reversal

Proof:

• If L is a CFL with grammar G , form a grammar for LR by reversing the body of every production.

Example:

Let G have S→0S1 | 01.
The reversal of L(G) has grammar S→ 1S0 | 10.

Closure of CFL's Under Homomorphism

Proof:

• Let L be a CFL with grammar G .
  Let h be a homomorphism on the terminal symbols of G .
  Construct a grammar for h(L) by replacing each terminal symbol a by h(a) .

Example:

G has productions S -> 0S1 | 01.
h is defined by h(0) = ab, h(1) = ε.
h(L(G)) has the grammar with productions S -> abS | ab.

Nonclosure Under Intersection

Proof:

• Unlike the regular languages, the class of CFL's is not closed under ∩ .
  We know that L1={0n1n2n|n≥1} is not a CFL (use the pumping lemma).
  However, L2={0n1n2i|n≥1,i≥1} is.
  CFG: S->AB, A->0A1|01, B->2B|2.
  So is L3={0i1n2n|n≥1,i≥1} .
  But L1=L2∩L3 .

Nonclosure Under Difference

Proof:

• We can prove something more general:
  Any class of languages that is closed under difference is closed under intersection.

  Proof: L ∩ M = L – (L – M).

  Thus, if CFL's were closed under difference, they would be closed under intersection, but they are not.

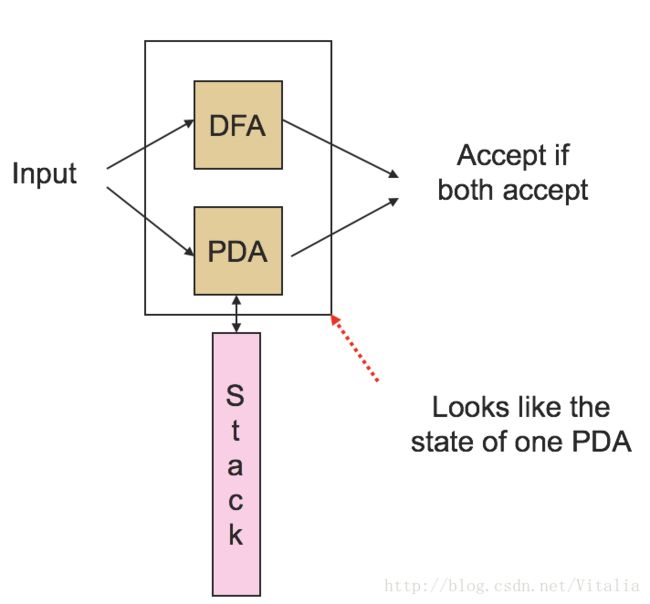
Intersection with a Regular Language

The intersection of a CFL with a regular language is always a CFL.
Proof:

• Run a DFA in parallel with a PDA.
• Note that the combination is a PDA.
• PDA's accept by final state.

DFA and PDA in Parallel

Formal Construction

• Let the DFA A have transition function δA .
• Let the PDA P have transition function δP .
  States of combined PDA are [q, p], where q is a state of A and p a state of P.
  δ([q,p],a,X) contains ( [δA(q,a),r],α ) if δP(p,a,X) contains (r,α ).
  
  • Note a could be ϵ , in which case δA(q,a)=q .
• Final states of combined PDA are those [q,p] such that q is a final state of A and p is an accepting state of P .
• Initial state is the pair [q0,p0] consisting of the initial states of each.
• Easy induction:
  
  • ([q0,p0],w,Z0)⊦∗([q,p],ϵ,α) iff δA(q0,w)=q
  • (p0,w,Z0)⊦∗(p,ϵ,α) in P .