各种排序算法(In-place sort)
常用排序算法的时间复杂度和空间复杂度表格
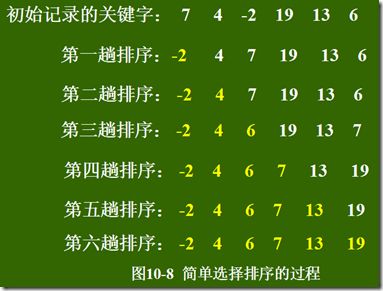
1.选择排序
思想:每次找一个最小值。
#include
using namespace std;
//从小到大排序
void SelectSort(int a[], int n)
{
int index, temp;
for (int i = 0; i < n - 1; i++) //执行(n-1) 次
{
index = i;
for (int j = i + 1; j a[j]) //记录序列中最小值的位置
{
index = j;
}
}
if (index != i) //如果无序序列中第一个记录不是最小值,则进行交换
{
temp = a[index];
a[index] = a[i];
a[i] = temp;
}
}
}
int main()
{
int a[10], i, n = 10, num = 10;
for (i = 0; i < n; i++)
a[i] = num--;
cout << "原序列:\n";
for (i = 0; i < n; i++)
cout << a[i] << " ";
SelectSort(a, n); cout << "排序后:\n"; for (i = 0; i < n; i++)cout << a[i] << " ";
return 0;
}
//优化排序
//如果在每一次查找最小值的时候,也可以找到一个最大值,然后将两者分别放在它们应该出现的位置,这样遍历的次数就比较少了,下边
//给出代码实现:
void SelectSort2(int a[], int n) {
int left = 0; int right = n - 1; int min = left;//存储最小值的下标
int max = left;//存储最大值的下标
while (left <= right)
{
min = left;
max = left;
for (int i = left; i <= right; ++i)
{
if (a[i] < a[min])
min = i;
if (a[i] > a[max]) max = i;
}
swap(a[left], a[min]);
if (left == max)
max = min;
swap(a[right], a[max]);
++left;
--right;
}
}
//递归版
void RecursiveSelectSort(int a[], int start, int end)
{
if (start < end)
{
int temp = a[start];
int index = start;
for (int i = start + 1; i < end; i++)
{
if (a[index] > a[i])
{
index = i;
}
}
if (start != index)
{
temp = a[start];
a[start] = a[index];
a[index] = temp;
}
start++;
RecursiveSelectSort(a, start, end);
}
}
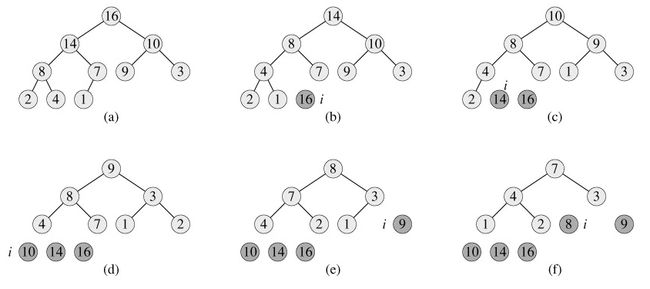
2.堆排序
思想:一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数,
二是反复调用渗透函数实现排序的函数。
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void HeapAdjust(int *a, int i, int size) //调整堆
{
int lchild = 2 * i; //i的左孩子节点序号
int rchild = 2 * i + 1; //i的右孩子节点序号
int max = i; //临时变量
if (i <= size / 2) //如果i不是叶节点就不用进行调整
{
if (lchild <= size&&a[lchild] > a[max])
{
max = lchild;
}
if (rchild <= size&&a[rchild] > a[max])
{
max = rchild;
}
if (max != i)
{
swap(a[i], a[max]);
HeapAdjust(a, max, size); //避免调整之后以max为父节点的子树不是堆
}
}
}
void BuildHeap(int *a, int size) //建立堆
{
int i;
for (i = size / 2; i >= 1; i--) //非叶节点最大序号值为size/2
{
HeapAdjust(a, i, size);
}
}
void HeapSort(int *a, int size) //堆排序
{
int i;
BuildHeap(a, size);
for (i = size; i >= 1; i--)
{
swap(a[1], a[i]); //交换堆顶和最后一个元素,即每次将剩余元素中的最大者放到最后面
HeapAdjust(a, 1, i - 1); //重新调整堆顶节点成为大顶堆
}
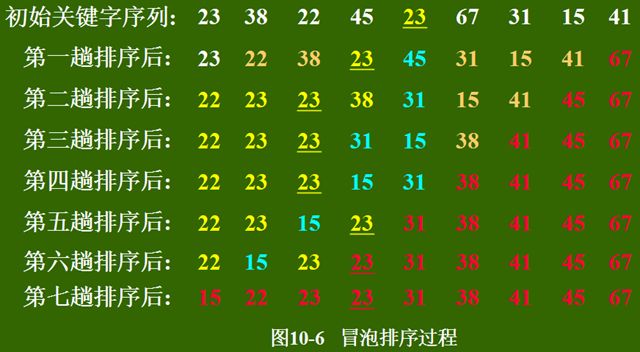
}3.冒泡排序
思想:通过两两交换,像水中的泡泡一样,小的先冒出来,大的后冒出来,每一次都有一个相对的最大值沉底。
void BubbleSort(int a[], int n)
{
int temp;
for (int i = 0; i < n - 1; i++) //执行(n-1)次 每一次冒泡 都有一个最大值沉底
{
for (int j = 0; j< n - i - 1; j++) //执行(n-1)次 冒泡的次数 决定冒泡的位置
{
if (a[j]>a[j + 1])
{
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
//改进的冒泡排序
//最佳运行时间:O(n)
//最坏运行时间:O(n^2)
void BubbleSort2(int a[], int n)
{
int temp,flag = 0;
for (int i = 0; i < n - 1; i++) //每一次冒泡 都有一个最大值沉底
{
for (int j = 0; ja[j + 1])
{
flag = 1;
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
if (flag == 0)
break; //没有数据交换 已经排好序了
}
}
//改进2传统冒泡排序中每一趟排序操作只能找到一个最大值或最小值,我们考虑利用在每趟排序中进行正向和反向两遍冒泡的方法一次
//可以得到两个最终值(最大者和最小者) , 从而使排序趟数几乎减少了一半。
void Bubble_2(int a[], int n)
{
int low = 0;
int high = n - 1; //设置变量的初始值
int tmp, j;
while (low < high)
{
for (j = low; j< high; ++j) //正向冒泡,找到最大者
if (a[j]> a[j + 1])
{
tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
--high; //修改high值, 前移一位
for (j = high; j>low; --j) //反向冒泡,找到最小者
if (a[j] < a[j - 1])
{
tmp = a[j];
a[j] = a[j - 1];
a[j - 1] = tmp;
}
++low; //修改low值,后移一位
}
}
//递归冒泡排序
void RecursiveBubbleSort(int a[], int start, int end)
{
if (start < end) //循环结束条件一为start == end
{
int temp = 0;
int length = end - start + 1;
for (int i = start; i < length - 1; i++) //循环结束条件二为i < length - 1;
{
if (a[i] < a[i + 1])
{
temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
}
}
end--;
RecursiveBubbleSort(a, start, end);
}
} 4.快速排序
思想:选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟排序讲待排序的记录分割成独立的两部分,其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。用同样的方法继续进行排序,直到整个序列有序。
void Swap(int *p1, int *p2)
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
void QuickSort(int *arr, int ileft, int iright, int length)
{
int i = ileft;//从左边开始循环
int j = iright + 1;//从右边开始循环
if (i < j)
{
do
{
do
{
i++;
} while (arr[i] <= arr[ileft] && i <= iright);
do
{
j--;
} while (arr[j] >= arr[ileft] && j > ileft);
if (i < j)
{
Swap(&arr[i], &arr[j]);
}
} while (i < j);
Swap(&arr[ileft], &arr[j]);
QuickSort(arr, ileft, j - 1, 0);
QuickSort(arr, j + 1, iright, 0);
}
}
//改进快排
void Swap(int *p1, int *p2)
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
int partition(int a[], int low, int high)
{
int privotKey = a[low]; //基准元素
while (low < high){ //从表的两端交替地向中间扫描
while (low < high && a[high] >= privotKey)
--high; //从high 所指位置向前搜索,至多到low+1 位置。将比基准元素小的交换到低端
Swap(&a[low], &a[high]);
while (low < high && a[low] <= privotKey)
++low;
Swap(&a[low], &a[high]);
}
return low;
}
void qsort_improve(int r[], int low, int high, int k)
{
if (high - low > k)
{ //长度大于k时递归, k为指定的数
int pivot = partition(r, low, high); // 调用的Partition算法保持不变
qsort_improve(r, low, pivot - 1, k);
qsort_improve(r, pivot + 1, high, k);
}
}
void quickSort(int r[], int n, int k)
{
qsort_improve(r, 0, n, k);//先调用改进算法Qsort使之基本有序
//再用插入排序对基本有序序列排序
for (int i = 1; i <= n; i++){
int tmp = r[i];
int j = i - 1;
while (tmp < r[j])
{
r[j + 1] = r[j];
j = j - 1;
}
r[j + 1] = tmp;
}
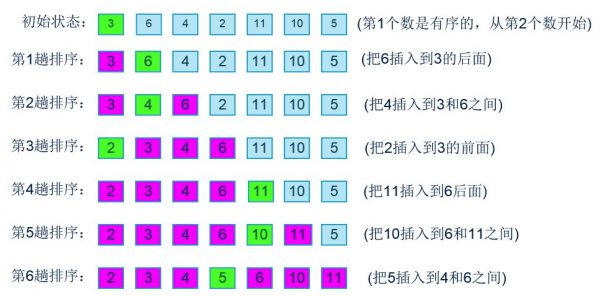
}5.插入排序
思想:假设待排序的记录存放在数组R[1..n]中。初始时,R[1]自成1个有序区,无序区为R[2..n]。从i=2起直至i=n为止,依次将R[i]插入当前的有序区R[1..i-1]中,生成含n个记录的有序区。
void InsertSort(int a[], int n)
{
for (int i = 2; i <=n; i++) //外循环(n-1)次
{
int j = i - 1; // 从下标为1开始
a[0] = a[i]; //每个数都要与a[0](相当于key)比较
while (a[0]0) //比a[0]大,则替换
{
a[j + 1] = a[j];
j--; //向前移动一位,再进行比较
}
a[j + 1] = a[0];
}
}
int main()
{
int a[20], i, n =10;
int num = 10;
for (i = 1; i <=10; i++)
a[i] = num--;
cout << "原序列:\n";
for (i = 1; i <=n; i++)
cout << a[i] << " ";
cout << endl;
InsertSort(a, 10);
cout << "排序后:\n";
for (i = 1; i <=n; i++)
cout << a[i] << " ";
return 0;
} 6.希尔排序
思想:先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放///在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2
void ShellSort(int a[], int n)
{
int d = n / 2;
while (d >= 1)
{
for (int i = 2 + d; i <= n; i++)
{
int j = i - d;
a[0] = a[i];
while (j > 0 && a[0] < a[j])
{
a[j + d] = a[j];
j = j - d;
}
a[j + d] = a[0];
}
d = d / 2;
}
}
int main()
{
int a[20], i, n =10;
int num = 10;
for (i = 1; i <=10; i++)
a[i] = num--;
cout << "原序列:\n";
for (i = 1; i <=n; i++)
cout << a[i] << " ";
cout << endl;
ShellSort(a, 10);
cout << "排序后:\n";
for (i = 1; i <=n; i++)
cout << a[i] << " ";
return 0;
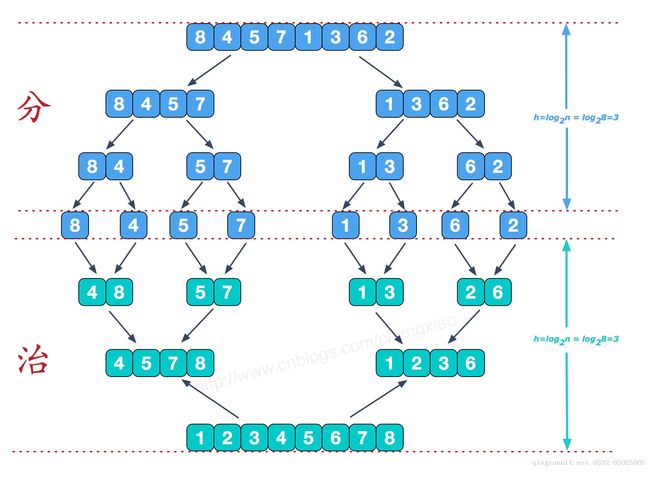
}7.归并排序法
思想:将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
//将r[i…m]和r[m +1 …n]归并到辅助数组b[i…n]
void Merge(int *a, int *b, int i, int m, int n)
{
int j, k;
for (j = m + 1, k = i; i <= m && j <= n; ++k)
{
if (a[j] < a[i])
b[k] = a[j++];
else
b[k] = a[i++];
}
while (i <= m)
b[k++] = a[i++];
while (j <= n)
b[k++] = a[j++];
}
void MergeSort(int *a, int *b, int lenght)
{
int len = 1;
int *q = a;
int *tmp;
while (len < lenght)
{
int s = len;
len = 2 * s;
int i = 0;
while (i + len < lenght)
{
Merge(q, b, i, i + s - 1, i + len - 1); //对等长的两个子表合并
i = i + len;
}
if (i + s < lenght)
Merge(q, b, i, i + s - 1, lenght - 1); //对不等长的两个子表合并
tmp = q; q = b; b = tmp; //交换q,b,以保证下一趟归并时,仍从q 归并到b
}
}
int main()
{
int a[10] = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 };
int b[10];
cout << "原序列:\n";
for (int i = 0; i < 10; i++)
cout << a[i] << " ";
cout << endl;
MergeSort(a, b, 10);
cout << "排序后:\n";
for (int i = 0; i < 10; i++)
cout << a[i] << " ";
return 0;
}
//两路归并
//思想设两个有序的子文件(相当于输入堆)放在同一向量中相邻的位置上:R[low..m],R[m+1..high],先将它们合并到
//一个局部的暂存向量R1(相当于输出堆)中,待合并完成后将R1复制回R[low..high]中。
//merge two subArray,one is A[i1]~A[j1],another is A[i2]~A[j2]
void MergeTwoArray(int A[], int i1, int j1, int i2, int j2)
{
int *tmp = new int[j2 - i1 + 1];
int i = i1, j = i2, k = 0;
while (i <= j1 && j <= j2)
{
//add samller one into tmp arrary
if (A[i] <= A[j])
{
tmp[k++] = A[i++];
}
else
{
tmp[k++] = A[j++];
}
}
while (i <= j1)
tmp[k++] = A[i++];
while (j <= j2)
tmp[k++] = A[j++];
for (i = 0; i < k; i++)
{
A[i1++] = tmp[i];
}
delete[]tmp;
}
void MergeSort(int A[], int n)
{
int i1, j1, i2, j2 = 0;
int size = 1;
while (size < n)
{
i1 = 0;
while (i1 + size < n)//存在两个序列,那就需要合并
{
//确定两个序列的边界
j1 = i1 + size - 1;
i2 = i1 + size;
if (i2 + size - 1 > n - 1)
{
j2 = n - 1;
}
else
j2 = i2 + size - 1;
MergeTwoArray(A, i1, j1, i2, j2);
//更新i1
i1 = j2 + 1;
}
size *= 2;
}
}
int main()
{
int a[10] = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 };
cout << "原序列:\n";
for (int i = 0; i < 10; i++)
cout << a[i] << " ";
cout << endl;
MergeSort(a, 10);
cout << "排序后:\n";
for (int i = 0; i < 10; i++)
cout << a[i] << " ";
return 0;
}8.(桶)基数排序
思想:基数排序是通过“分配”和“收集”过程来实现排序。
int getdigit(int x, int d)
{
int a[] = { 1, 1, 10 }; //因为待排数据最大数据也只是两位数,所以在此只需要到十位就满足
return ((x / a[d]) % 10); //确定桶号
}
void msdradix_sort(int arr[], int begin, int end, int d)
{
const int radix = 10;
int count[radix], i, j;
//置空
for (i = 0; i < radix; ++i)
{
count[i] = 0;
}
//分配桶存储空间
int *bucket = (int *)malloc((end - begin + 1) * sizeof(int));
//统计各桶需要装的元素的个数
for (i = begin; i <= end; ++i)
{
count[getdigit(arr[i], d)]++;
}
//求出桶的边界索引,count[i]值为第i个桶的右边界索引+1
for (i = 1; i < radix; ++i)
{
count[i] = count[i] + count[i - 1];
}
//这里要从右向左扫描,保证排序稳定性
for (i = end; i >= begin; --i)
{
j = getdigit(arr[i], d); //求出关键码的第d位的数字, 例如:576的第3位是5
bucket[count[j] - 1] = arr[i]; //放入对应的桶中,count[j]-1是第j个桶的右边界索引
--count[j]; //第j个桶放下一个元素的位置(右边界索引+1)
}
//注意:此时count[i]为第i个桶左边界
//从各个桶中收集数据
for (i = begin, j = 0; i <= end; ++i, ++j)
{
arr[i] = bucket[j];
}
//释放存储空间
free(bucket);
//对各桶中数据进行再排序
for (i = 0; i < radix; i++)
{
int p1 = begin + count[i]; //第i个桶的左边界
int p2 = begin + count[i + 1] - 1; //第i个桶的右边界
if (p1 < p2 && d > 1)
{
msdradix_sort(arr, p1, p2, d - 1); //对第i个桶递归调用,进行基数排序,数位降 1
}
}
}
int main()
{
int a[10] = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 };
cout << "原序列:\n";
for (int i = 0; i < 10; i++)
cout << a[i] << " ";
cout << endl;
msdradix_sort(a, 0, 10 - 1, 2);
cout << "排序后:\n";
for (int i = 0; i < 10; i++)
cout << a[i] << " ";
return 0;
}