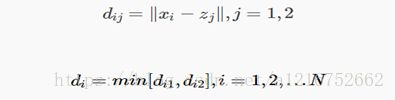基于C++的最大最小聚类算法实现

一、          算法简介

1.   简介：

最大最小距离法是模式识别中一种基于试探的类聚算法，它以欧式距离为基础，取尽可能远的对象作为聚类中心。因此可以避免K-means法初值选取时可能出现的聚类种子过于临近的情况，它不仅能智能确定初试聚类种子的个数，而且提高了划分初试数据集的效率。

    该算法以欧氏距离为基础，首先初始一个样本对象作为第1个聚类中心，再选择一个与第1个聚类中心最远的样本作为第2个聚类中心，然后确定其他的聚类中心，直到无新的聚类中心产生。最后将样本按最小距离原则归入最近的类。

2.   算法流程

1)       从N个样本集中的任选取一个样本，作为第一个聚类中心z1；

2)       选取距离第一个聚类中心z1最远的样本作为第二个聚类中心z2；

3)       计算其余样本与z1、z2之间的距离，并求出它们中的最小值，即：

 

4)       若：(θ为选定的比例系数)

则相应的样本xl作为第三个聚类中心z3,转至下一步继续判断是否存在新的聚类中心，否则转至第六步；

5)       假设存在k个聚类中心，计算各样本到各个聚类中心的距离dij，并算出：

若成立，则zk+1=xl,并循环此步骤，继续判断是否有新的聚类中心存在，否则转至第六步；

6)       当判断不再有新的聚类中心存在时，将样本集按最小距离原则分到各类中去，即计算：

二、          算法实现

1.   实验数据—data.txt

l  文件内容

d=2 n=150

5.1  3.5

4.9  3

4.7  3.2

4.6  3.1

…

l  数据说明

第一行为特征维度数量和数据数量，此次试验是150个2维数据。数据来源于IRIS数据集的前两个特征。

 

还应该手动输入比例系数θ（0-1）.

2.   输出数据—result.txt

输出数据输出实验数据聚类后的分类信息，与真实信息对比来分析程序聚类准确率。

l  文件内容：

0

2

0

1

0

              …

l  数据说明：

0，1，2依次对应表示Setosa，Versicolour，Virginica三类花。

3.   程序运行截图

l  Θ=0.5时：

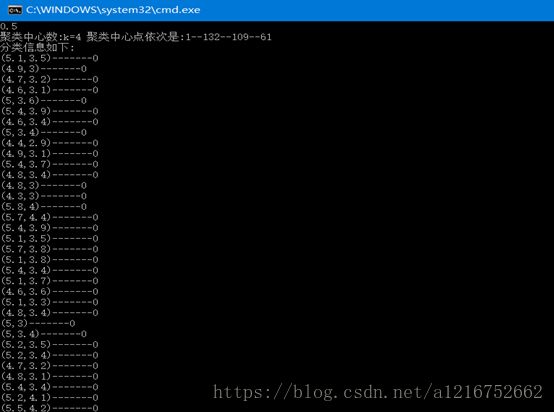
数据被分为4类，并输出了聚类中心标号

l  Θ=0.6时：

                                            图2

       数据被分为3类，并输出了聚类中心标号

4.   结果分析：

将输出的result.txt文件导入EXCEL与真实信息对比计算。150个数据中有133个与真实数据的分类信息吻合，两次Θ取值，都只有83个样本正确，正确率只有55.33%

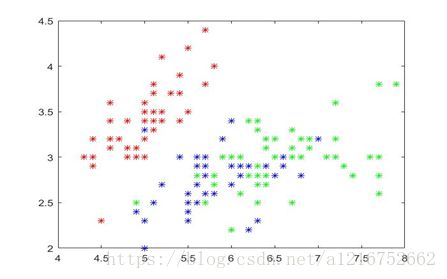
       我认为出现该结果的原因是因为样本特征选取不够，IRIS花瓣集前两个特征差异性不大。如图，为前两个特征的散点分布图有较多重合。在我的另一组测试数据中，当样本间距够大时能达到很好的分类效果（但样本数量太少没有采用来作为数据集）。

图3.IRIS数据集

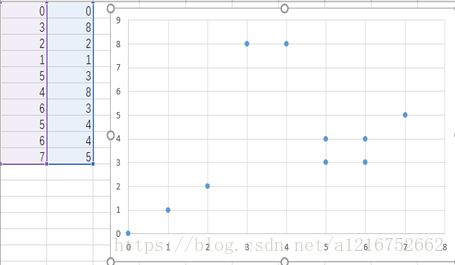
图4.另一组数据集

              在这个数据集下表现良好，数据都能完美分开，但数量太少，不作过多讨论

5.   C++源码：

#include   
#include   
using namespace std;

const int N=150;//给定N个样本

int maxmindistance(float *sample[N],float theta)  
{ 
	int center[20];//保存聚类中心  
	float D[20][N];//保存D点与点之间的距离  

	float min[N];  //始终保存各点到各个聚类中心最小的距离
	int minindex[N];  

	int clas[N];  

	float theshold;  
	float D12=0.0;//第一个聚类和第二个聚类中的距离  
	float tmp=0;  
	int index=0;  
	center[0]=0;//first center第一个聚类选出来了  
	int i,k=0,j,m;  


	//计算其他样本到第一个聚类中心（0，0）的距离  
	//D[0][j]保存第j个点到到第1个聚类中心的距离
	for(j=0;jD12)
		{
			D12=D[0][j];
			index=j;
		}  //求出距离第一个聚类中心最远的点
	}  



	center[1]=index;//second center第二个聚类中心选出来了 并保存 
	k=1;  
	index=0;  
	theshold=D12;//两个聚类中心的距离 
	//最新的两聚类中心距离大于θ*D12则继续选取聚类中心
	while(theshold>theta*D12)  
	{  
		for(j=0;jmax) 
			{
				max=min[j];      //找到最大的
				index=j;         //并找到相应的点的下标
			}  
			if (max>theta*D12)
			{
				k++;
				center[k]=index;
			}// add a center  
			theshold=max;// prepare to loop next time  
	}  //求出所有中心,final array min[] is still useful  

	for(j=0;j>theta;
	maxmindistance(data,theta);
}