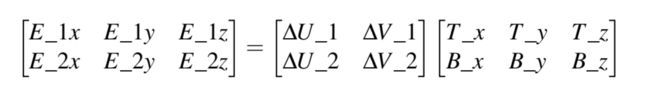LearnOpenGL 总结记录 Normal Mapping

Tangent space（切线空间）

Normal vectors in a normal map are expressed in tangent space where normals always point roughly in the positive z direction.

Calculating the tangent and bitangent vectors is not as straightforward as the normal vector. We can see from the image that the direction of the normal map’s tangent and bitangent vector align with the direction in which we define a surface’s texture coordinates. We’ll use this fact to calculate tangent and bitangent vectors for each surface. Retrieving them does require a bit of math; take a look at the following image:

From the image we can see that the texture coordinate differences of an edge E_2 of a triangle denotes as ∆U _2 and ∆V _2 are expressed in the same direction as the tangent vector T and bitangent vector B. Because of this we can write both displayed edges E_1 and E_2 of the triangle as a linear combination of the tangent vector T and the bitangent vector B:

1. （用两个不同的空间来表示同一个点 的坐标变换公式来推导）

 

2. 

3. 

4.

 

5. 

 

Don’t worry if you don’t really understand the mathematics behind this. As long as you understand that we can calculate tangents and bitangents from a triangle’s vertices and its texture coordinates (since texture coordinates are in the same space as tangent vectors) you’re halfway there.

上面的就是 说明如何生成一个三角形的 切线空间的 T，B 基。

 

应用

下面的就是指用利用上面的公式来计算三角形自身的 切线空间下的法线，切线，副法线

// positions
        glm::vec3 pos1(-1.0f,  1.0f, 0.0f);
        glm::vec3 pos2(-1.0f, -1.0f, 0.0f);
        glm::vec3 pos3( 1.0f, -1.0f, 0.0f);
        glm::vec3 pos4( 1.0f,  1.0f, 0.0f);
        // texture coordinates
        glm::vec2 uv1(0.0f, 1.0f);
        glm::vec2 uv2(0.0f, 0.0f);
        glm::vec2 uv3(1.0f, 0.0f);  
        glm::vec2 uv4(1.0f, 1.0f);
        // normal vector
        glm::vec3 nm(0.0f, 0.0f, 1.0f);

        // calculate tangent/bitangent vectors of both triangles
        glm::vec3 tangent1, bitangent1;
        glm::vec3 tangent2, bitangent2;
        // triangle 1
        // ----------
        glm::vec3 edge1 = pos2 - pos1;
        glm::vec3 edge2 = pos3 - pos1;
        glm::vec2 deltaUV1 = uv2 - uv1;
        glm::vec2 deltaUV2 = uv3 - uv1;

        GLfloat f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);

        tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
        tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
        tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
        tangent1 = glm::normalize(tangent1);

        bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
        bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
        bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
        bitangent1 = glm::normalize(bitangent1);

        // triangle 2
        // ----------
        edge1 = pos3 - pos1;
        edge2 = pos4 - pos1;
        deltaUV1 = uv3 - uv1;
        deltaUV2 = uv4 - uv1;

        f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);

        tangent2.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
        tangent2.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
        tangent2.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
        tangent2 = glm::normalize(tangent2);


        bitangent2.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
        bitangent2.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
        bitangent2.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
        bitangent2 = glm::normalize(bitangent2);


        float quadVertices[] = {
            // positions            // normal         // texcoords  // tangent                          // bitangent
            pos1.x, pos1.y, pos1.z, nm.x, nm.y, nm.z, uv1.x, uv1.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
            pos2.x, pos2.y, pos2.z, nm.x, nm.y, nm.z, uv2.x, uv2.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
            pos3.x, pos3.y, pos3.z, nm.x, nm.y, nm.z, uv3.x, uv3.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,

            pos1.x, pos1.y, pos1.z, nm.x, nm.y, nm.z, uv1.x, uv1.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z,
            pos3.x, pos3.y, pos3.z, nm.x, nm.y, nm.z, uv3.x, uv3.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z,
            pos4.x, pos4.y, pos4.z, nm.x, nm.y, nm.z, uv4.x, uv4.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z
        };
        // configure plane VAO
        glGenVertexArrays(1, &quadVAO);
        glGenBuffers(1, &quadVBO);
        glBindVertexArray(quadVAO);
        glBindBuffer(GL_ARRAY_BUFFER, quadVBO);
        glBufferData(GL_ARRAY_BUFFER, sizeof(quadVertices), &quadVertices, GL_STATIC_DRAW);
        glEnableVertexAttribArray(0);
        glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 14 * sizeof(float), (void*)0);
        glEnableVertexAttribArray(1);
        glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 14 * sizeof(float), (void*)(3 * sizeof(float)));
        glEnableVertexAttribArray(2);
        glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 14 * sizeof(float), (void*)(6 * sizeof(float)));
        glEnableVertexAttribArray(3);
        glVertexAttribPointer(3, 3, GL_FLOAT, GL_FALSE, 14 * sizeof(float), (void*)(8 * sizeof(float)));
        glEnableVertexAttribArray(4);
        glVertexAttribPointer(4, 3, GL_FLOAT, GL_FALSE, 14 * sizeof(float), (void*)(11 * sizeof(float)));

 

渲染

ps：

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;

out VS_OUT {
    vec3 FragPos;
    vec2 TexCoords;
    vec3 TangentLightPos;
    vec3 TangentViewPos;
    vec3 TangentFragPos;
} vs_out;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

uniform vec3 lightPos;
uniform vec3 viewPos;

void main()
{
    vs_out.FragPos = vec3(model * vec4(aPos, 1.0));   
    vs_out.TexCoords = aTexCoords;
    
    mat3 normalMatrix = transpose(inverse(mat3(model)));
    vec3 T = normalize(normalMatrix * aTangent);
    vec3 N = normalize(normalMatrix * aNormal);
    T = normalize(T - dot(T, N) * N);
    vec3 B = cross(N, T);
    
    mat3 TBN = transpose(mat3(T, B, N));    
    vs_out.TangentLightPos = TBN * lightPos;
    vs_out.TangentViewPos  = TBN * viewPos;
    vs_out.TangentFragPos  = TBN * vs_out.FragPos;
        
    gl_Position = projection * view * model * vec4(aPos, 1.0);
}

1. aTangent，aNormal 都是来自于切线空间，是计算出来的。

 

2. 这里其实就是 先 构造一个TBN，切线空间矩阵，然后把lightPos，viewPos 都变换到 切线空间进行计算。

以下的代码值得注意：

T = normalize(T - dot(T, N) * N); //作用就是 re-orthogonalize the TBN vectors

When tangent vectors are calculated on larger meshes that share a considerable amount of vertices the tangent vectors are generally averaged to give nice and smooth results when normal mapping is applied to these surfaces. A problem with this approach is that the three TBN vectors could end up non-perpendicular to each other which means the resulting TBN matrix would no longer be orthogonal. Normal mapping will be only slightly off with a non-orthogonal TBN matrix, but it’s still something we can improve.

Using a mathematical trick called the Gram-Schmidt process we can re-orthogonalize the TBN vectors such that each vector is again perpendicular to the other vectors. Within the vertex shader we would do it like this:

vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
// re-orthogonalize T with respect to N
T = normalize(T - dot(T, N) * N);
// then retrieve perpendicular vector B with the cross product of T and N
vec3 B = cross(N, T);
mat3 TBN = mat3(T, B, N)

This, albeit by a little, generally improves the normal mapping results with a little extra cost. Take a look at the end of the Normal Mapping Mathematics video referenced below this tutorial for a great explanation of how this process actually works.

 

 

 

 

fs：

#version 330 core
out vec4 FragColor;

in VS_OUT {
    vec3 FragPos;
    vec2 TexCoords;
    vec3 TangentLightPos;
    vec3 TangentViewPos;
    vec3 TangentFragPos;
} fs_in;

uniform sampler2D diffuseMap;
uniform sampler2D normalMap;

uniform vec3 lightPos;
uniform vec3 viewPos;

void main()
{           
     // obtain normal from normal map in range [0,1]
    vec3 normal = texture(normalMap, fs_in.TexCoords).rgb;
    // transform normal vector to range [-1,1]
    normal = normalize(normal * 2.0 - 1.0);  // this normal is in tangent space
   
    // get diffuse color
    vec3 color = texture(diffuseMap, fs_in.TexCoords).rgb;
    // ambient
    vec3 ambient = 0.1 * color;
    // diffuse
    vec3 lightDir = normalize(fs_in.TangentLightPos - fs_in.TangentFragPos);
    float diff = max(dot(lightDir, normal), 0.0);
    vec3 diffuse = diff * color;
    // specular
    vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos);
    vec3 reflectDir = reflect(-lightDir, normal);
    vec3 halfwayDir = normalize(lightDir + viewDir);  
    float spec = pow(max(dot(normal, halfwayDir), 0.0), 32.0);

    vec3 specular = vec3(0.2) * spec;
    FragColor = vec4(ambient + diffuse + specular, 1.0);
}