学习算法和数据结构：栈和队列

「学习算法和数据结构系列」，栈和队列同属于线性结构

---

栈和队列的特点

栈：LIFO（后进先出）
队列：FIFO（先进先出）

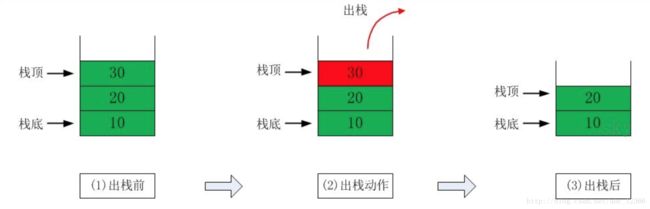
栈是限定仅在表尾进行插入和删除的线性表
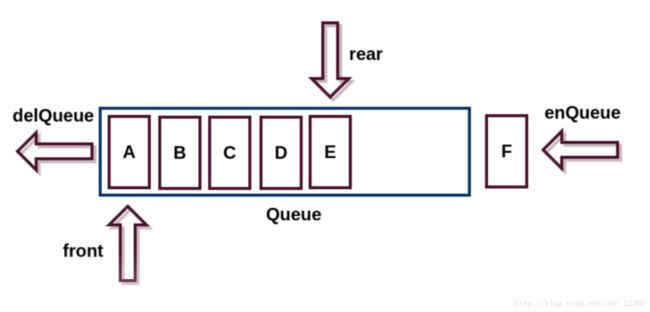
队列是仅允许在一端插入在另一端删除的线性表

不论栈还是队列都是一种访问受限制的线性表

*补充：给定n个数，求所有可能的出栈顺序种类数；公式如下图所示：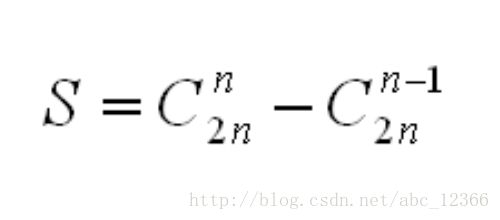
这可以看作是卡特兰数的一个应用，证明戳这里：http://blog.sina.com.cn/s/blog_6917f47301010cno.html（文章不长，不是我写的）

---

栈和队列的代码实现

不同的数据结构说白了就是一些包含系列操作集的数据集合

栈的特有操作集：弹栈（Pop），压栈（Push）
队列的特有操作集：进队列，出队列

不论栈还是队列都可以用“数组”或者“链表”来实现（顺序存储+链式存储）

栈的ADT

//ADT
Data
    同线性表；元素具有相同的类型，相邻元素间具有前趋和后继结点
Operation
    InitStack(*S)：初始化操作，建立一个空栈S
    DestroyStack(*S)：若栈存在，则销毁它
    ClearStack(S)：将栈清空
    StackEmpty(S)：若栈为空，返回true，否则返回false
    GetTop(S, *e)：若栈存在且非空，则用e返回栈顶元素
    Push(*S, e)：若栈S存在，插入新元素到栈S中并成为栈顶元素
    Pop(*S, *e)：删除栈S中的栈顶元素，并用e返回
    StackLength(S)：返回栈S的元素个数
endADT

栈的数组实现

typedef struct
{
    int data[MAXSIZE];  /*下标从0开始*/
    int top;  /*用于栈顶指针*/
}sqStack;

栈插入元素（进栈）

int Push(sqStack *S, int e)
{
    if(S->top == MAXSIZE-1){  /*栈满*/
        return -1;
    }
    S->top++;  /*栈顶指针增加一*/
    S->data[S->top] = e;  /*将新插入的元素赋值给栈顶空间*/
    return 0;
}

栈删除元素（出栈）

int Pop(sqStack *S, int *e)
{
    if(S->top == -1){
        return -1;
    }
    *e = S->data[S->top];  /*将要删除的元素赋值给e*/
    S->top--;  /*栈顶指针减一*/
    return 0;
}

栈的链表实现（链栈）

对于链表来说，不需要实现固定好大小，而且基本上不会出现没有空间的情况（除非计算机操作系统已经濒临死机崩溃）

typedef struct _snode
{
    int data;
    struct _snode *next;
}SNode, *LinkStackPtr;

typedef struct
{
    LinkStackptr top;
    int count;
}LinkStack;

栈插入元素（进栈）

int Push(LinkStack *S, int e)
{
    LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode));
    s->data = e;
    s->next = S->top;
    S->top = s;
    S->count++;
    return 0;
}

栈删除元素（出栈）

int Pop(LinkStack *S, int e)
{
    LinkStackPtr p;
    if(StackEmpty(*S)){
        return -1;
    }
    *e = S->top->data;
    p = S->top;
    S->top = S->top->next;
    free(p);
    S->count++;
    return 0;
}

循环队列的ADT

//ADT
Data
    同线性表；元素具有相同的类型，相邻元素具有前趋和后继关系
Operation
    InitQueue(*Q)：初始化操作，建立一个空队列
    DestroyQueue(*Q)：若队列Q存在，则销毁它
    ClearQueue(*Q)：将队列Q清空
    QueueEmpty(Q)：若队列Q为空，则返true，否则返回false
    GetHead(Q, *e)：若队列Q存在且非空，用e返回队列Q的队头元素
    EnQueue(*Q)：若队列Q存在，插入新元素e到Q中并成为队尾元素
    DeQueue(*Q, *e)：删除队列Q中队头元素，并用e返回其值
endADT

循环队列的数组实现

typedef struct
{
    int data[MAXSIZE];
    int front;  /*头指针*/
    int rear;  /*尾指针，若队列不变，指向队列尾元素的下一个位置*/
}sqQueue;

循环队列初始化

int InitQueue(SqQueue *Q)
{
    Q->front = 0;
    Q->rear = 0;
    return 0;
}

循环队列长度

int QueueLength(sqQueue Q)
{
    return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

循环队列入队列

int EnQueue(sqQueue *Q, int e)
{
    if((Q->rear+1) % MAXSIZE == Q->front){  /*判断队列是否已满*/
        return -1;
    }
    Q->data[Q->rear] = e;  /*将e的值赋给队尾元素*/
    Q->rear = (Q->rear+1) % MAXSIZE;  /*rear指针向后移动一位，若到最后则转到数组的头部*/
    return 0;
}

循环队列出队列

int DeQueue(sqQueue *Q, int e)
{
    if(Q->front == Q->rear){  /*判断队列是否为空*/
        return -1;
    }
    *e = Q->data[Q->front];  /*将队头元素赋给e*/
    Q->front = (Q->front+1) % MAXSIZE;  /*front指针向后移动一位，若到最后则转到数组的头部*/
    return 0;
}

队列的链表实现（链队列）

typedef strut _qNode  /*结点结构*/
{
    int data;
    struct _qNode *next;
}QNode, *QueuePtr;

typedef struct  /*队列的链表结构（和栈一样的套路，先隔离再整体）*/
{
    QueuePtr front, rear;  /*队头、队尾指针*/
}LinkQueue;

元素入队

int EnQueue(LinkQueue *Q, int e)
{
    QueuePtr s = (QueuePtr)malloc(sizeof(QNode));
    if(!s){  /*内存分配失败*/
        exit(OVERFLOW);
    }
    s->data = e;
    s->next = NULL;
    Q->rear->next = s;  /*把拥有元素e的新结点s赋给原队尾结点的后继*/
    Q->rear = s;  /*把当前的s设置为队尾结点，rear指向s*/
    return 0;
}

元素出队

int DeQueue(LinkQueue *Q, int e)
{
    QueuePtr p;
    if(Q->front == Q->rear){
        return -1;
    }
    p = Q->front->next;  /*将要删除的队头结点暂存给p*/
    *e = p->data;  /*将要删除的队头结点赋给e*/
    Q->front->next = p->next;  /*将原队头结点后继p->next赋给头结点后继*/
    if(Q->rear == p){  /*若头结点是队尾，则删除后将rear指向头结点*/
        Q->rear == Q->front;
    }
    free(p);
    return 0;
}