chapter2 of OReilly.Hands－On.Machine.Learning.with.Scikit－Learn.and.TensorFlow

The process of one project:

1. Look at the big picture.
2. Get the data.
3. Discover and visualize the data to gain insights.
4. Prepare the data for Machine Learning algorithms.
5. Select a model and train it.
6. Fine-tune your model.
7. Present your solution.
8. Launch, monitor, and maintain your system.

Performance Measure :
A typical performance measure for regression problems is the Root Mean Square Error (RMSE). It measures thestandard deviation of the errors the system makes in its predictions. 

When a feature has a bell-shapednormal distribution(also called aGaussian distribution), which is very common, the “68-95-99.7” rule applies: about 68% of the values fall within 1σ of the mean, 95% within 2σ, and 99.7% within 3σ.

If there are many outlier districts. In that case, you may consider using theMean Absolute Error(also called the Average Absolute Deviation; seeEquation 2-2):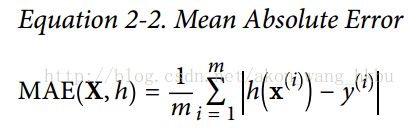

The higher the norm index, the more it focuses on large values and neglects small ones. This is why the RMSE is more sensitive to outliers than the MAE.  

如果要在jupter notebook中使用matplotlib，The simplest option is to use Jupyter’s magic command%matplotlib inline.

Different way to create test set:

Creating a test set is theoretically quite simple: just pick some instances randomly, typically 20% of the dataset, and set them aside:

import numpy as np
def split_train_test(data, test_ratio):
	shuffled_indices = np.random.permutation(len(data))
	test_set_size = int(len(data) * test_ratio)
	test_indices = shuffled_indices[:test_set_size]
	train_indices = shuffled_indices[test_set_size:]
	return data.iloc[train_indices], data.iloc[test_indices]

You can then use this function like this:

train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set), "train +", len(test_set), "test")
16512 train + 4128 test

Well, this works, but it is not perfect: if you run the program again, it will generate a different test set! Over time, you (or your Machine Learning algorithms) will get to see the whole dataset, which is what you want to avoid.

Another option is to set the random number generator’s seed (e.g.,np.random.seed(42))  before calling np.random.permutation(), so that it always generates the same shuffled indices.

But both these solutions will break next time you fetch an updated dataset. A common solution is to use each instance’s identifier to decide whether or not it should go in the test set (assuming instances have a unique and immutable identifier). For example, you could compute a hash of each instance’s identifier, keep only the last byte of the hash, and put the instance in the test set if this value is lower or equal to 51 (~20% of 256). This ensures that the test set will remain consistent across multiple runs, even if you refresh the dataset. The new test set will contain 20% of the new instances, but it will not contain any instance that was previously in the training set.

Here is a possible implementation:

import hashlib
def test_set_check(identifier, test_ratio, hash):
	return hash(np.int64(identifier)).digest()[-1] < 256 * test_ratio
def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5):
	ids = data[id_column]
	in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
	return data.loc[~in_test_set], data.loc[in_test_set]

Unfortunately, the housing dataset does not have an identifier column. The simplest solution is to use the row index as the ID:

housing_with_id = housing.reset_index() # adds an `index` column
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")

Using scikit-learn:

from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)

sklearn.model_selection模块中StratifiedShuffleSplit的example：

import numpy as np
from sklearn.model_selection import StratifiedShuffleSplit
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [8, 1], [7, 2], [5, 4], [6, 3], [1, 4], [2, 3]])
y = np.array([0, 0, 1, 1, 2, 2, 3, 3, 4 ,4])
sss = StratifiedShuffleSplit(n_splits=1, test_size=0.5, random_state=42)
print(sss, sss.get_n_splits(X, y))

StratifiedShuffleSplit(n_splits=1, random_state=42, test_size=0.5,
            train_size=None) 1

for train_index, test_index in sss.split(X, y):
    print("\n>TRAIN:", train_index, ">TEST:", test_index)
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    print(X_train)
    print("\n", X_test)
    print("\n", y_train, y_test)

>TRAIN: [7 2 5 1 9] >TEST: [3 0 6 8 4]
[[6 3]
 [1 2]
 [7 2]
 [3 4]
 [2 3]]


 [[3 4]
 [1 2]
 [5 4]
 [1 4]
 [8 1]]


 [3 1 2 0 4] [1 0 3 4 2]