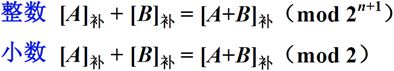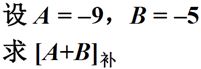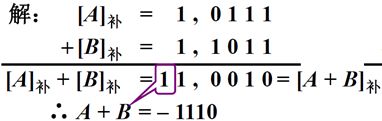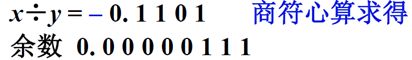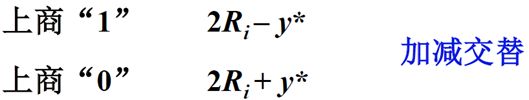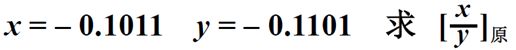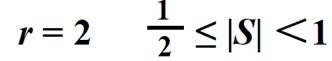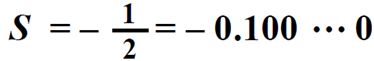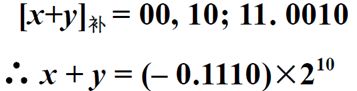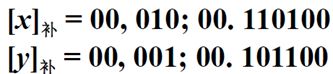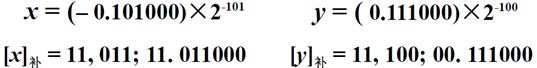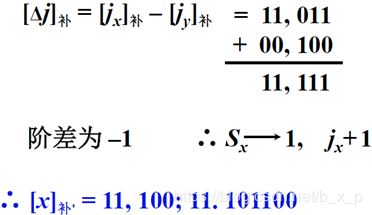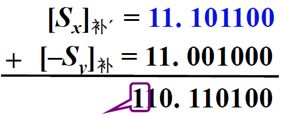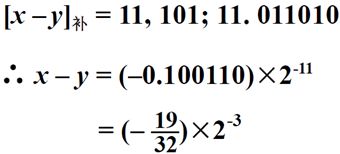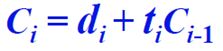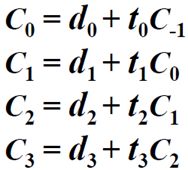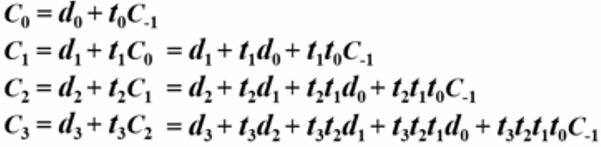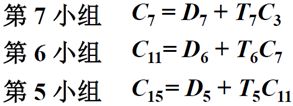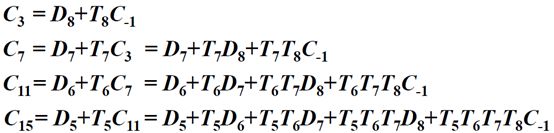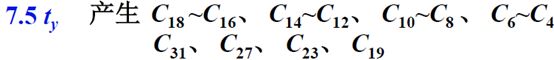定点运算，浮点运算，算术逻辑单元

定点运算

（一）移位运算

1、移位运算的数学意义
先举一个例子：15m = 1500 cm，在这个变换过程中，就可以通过移位运算进行实现，实际上在这个等式中，小数点被隐含了，在15m和1500cm数值最后有一个小数点被隐含掉没有体现出来， 在数学中我们说小数点向左或者向右移位，但是这样的说法在计算机中并不合适，在计算机中，小数点是以约定的方式给出的，在计算机中没有任何硬件用于表示小数点，所以在计算机中的移位指的是数据相对于小数点进行左移和右移，小数点位置不发生变化。所以有：

	左移一位	右移一位
十进制中	数据扩大为原来10倍	数据减小为原来10倍
二进制中	数据扩大为原来2倍	数据减小为原来2倍

在计算机中，移位和加减法配合实现乘除法运算。

2、算术移位规则
首先算数移位符号位不发生改变，移位规则如下：

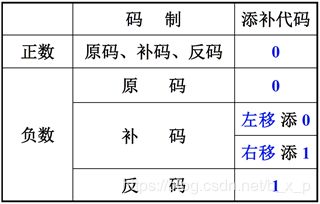
举例1：



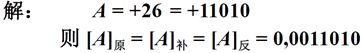
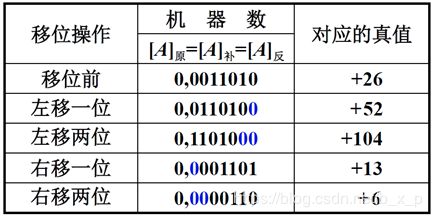
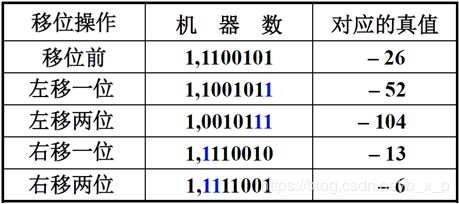
对于正数，三种机器数移位后符号位均不变，左移时最高数位丢1，结果出错，右移时最低数位丢1，影响精度。

举例2

原码：

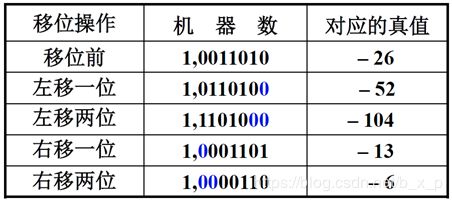
负数的原码左移时，高位丢1，结果出错，右移时，低位丢1，影响精度。

补码：

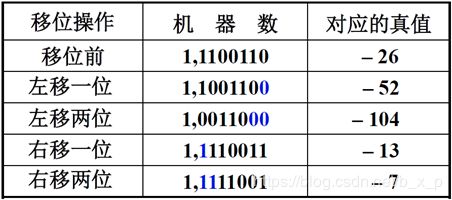
负数的补码左移时，高位丢0，结果出错；右移时，低位丢1，影响精度。

反码：

3、算术移位的硬件实现

真值为正数：
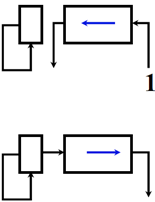
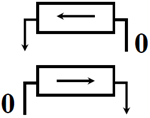
左移操作：符号位不变，左侧数值位扔掉，右侧补0。
右移操作：右侧数值位扔掉，最左侧补0，符号位也是0，这里可以在进行左侧添0的同时把符号位移动到数据最高位。电路如下：

负数原码移位电路：

负数补码移位电路：

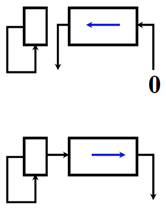
右移时，左侧补1，由于符号位也是1，在进行左侧补1同时可以将符号位移动到数据位最高位。

负数反码移位电路：

根据上面额移位规则和移位电路可以得出以下结论：

	真值为正	负数的原码	负数的补码	负数的反码
左移丢1	出错	出错	正确	正确
右移丢1	影响精度	影响精度	影响精度	正确

4、算术移位与逻辑移位的区别

算数移位：有符号数的移位
逻辑移位：无符号数的移位

所以有：

逻辑移位硬件实现如下：

举例：

（二）加减法运算

如果采用原码进行加减法运算会出现如下问题：

如上，同样是四种加法运算，实际上可能是加法也可能是减法，这是就需要找到一个和负数等价的整数代替负数，将减法运算转换为加法运算。所以采用补码进行加减法运算。

补码方式表示，我们主要利用了计算机中存放机器数的寄存器或者存储单元位位数有限的性质，如果加法和的范围超过了模能够表示的大小，最高位将会被丢掉，利用这样的性质，我们把减法变成了加法。因此在介绍计算机中的加减法运算的时候，我们介绍补码在计算机中的加减法是如何实现的。

先举一个例子证明一下：计算机中，正数A + 负数B = 正数A + [负数B]补。

如果计算机中的寄存器共5位，最高位表示符号位，计算8 – 1的推导过程如下：

所以得出：
1、 正数A + 负数B = 正数A + [负数B]补。
2、 在补码计算过程中，符号位要参与运算。
3、 计算得到的结果是补码，需要转换成原码读取真值。

1、加法运算公式

上面公式的简单证明：A和B都为负数情况下，将A和B转换成补码，分别需要加上2^( n+1)。而[A + B]结果的补码依然是给结果加上2 ^ ( n+1)，因为寄存器位数为n位，第n+1位被丢弃。所以左右依然相等。

2、减法运算公式

举例1：

举例2：

举例3：

举例4：

上面这个例子中，使用补码进行计算，得到的结果是错误的，错误的原码是：机器字长为八位，一位符号位，它能够表示的数据范围是[-128, 127]，共256个数，真实计算结果是-138，超出了这种机器数表示方式能够表示的范围，这种属于溢出。

3、加减法中溢出判断：

（1） 一位符号位判溢出

首先，一个正数和一个负数进行加法运算，其结果不可能发生溢出。参加操作的两个数符号相同（同正同负），其结果的符号与原操作数的符号不同，即为溢出。

这种判断溢出的硬件实现：

对于上面给出的硬件实现，如果两个加数相加：

如果是两个正数，符号位都是0，数值的最高位如果产生了进位，进位为1，这个进位会进到符号位，符号位有0变为1并且符号位不会向上产生进位，那就是说，最高有效位的进位 = 1，符号位进位 = 0，这种情况就会产生溢出。

如果两个操作数都是负数，如果数值的最高位向上没有进位 = 0，因为符号位都是1，所以符号位会向上进位 = 1，这种情况下就会产生溢出 。

如果我们采用这种方式判断溢出，我们就要使用硬件记录最高有效位的进位和符号位的进位，把这两个进位送入到一个异或电路，如果异或电路输出为1，则判断为溢出，输出为0，无溢出。

（2） 两位符号位判断溢出

如果是小数定点机中的加法运算，将补码的模由2变为4，则有：

经过上面这种变换，对于负数，数字两位符号位就变成了两个1。
如果是整数，原来是以2 ^ (n+1)为模，如果使用双符号位，模就变成2^(n+2)。
实际上，对于小数，还可以以2,4,8…2 ^ k为模，这种情况下，符号位就占用了K位。对于整数，可以以2^(n+m)为模，符号为占用m位，正数情况下，符号位为m个0，负数符号位是m个1。

以4为模情况下，加减法运算公式依然满足：

判断是否溢出的方法：

4、补码加法硬件配置：

上图中，A、X 均 n+1 位，核心是n+1位的加法器，由他完成了两个补码的加法运算，另外有两个寄存器：

ACC：保存被加数或被减数
X：保存的是加数或者减数
求两个数a与b的和时，第一个数a叫被加数，第二个数b叫加数。被减数和减数同理。

GA和GS是两个标记，如果做加法，将GA置1 ，如果是减法GS置1。

求补控制逻辑：为了支持减法运算，因为在减法过程中我们要完成从B的补码到-B的补码的转换，所以需要求补控制逻辑。这个求补控制逻辑就完成了X中保存的数据如果是减法运算，就将其每位取反（包括符号位），那求补过程最后的加1的操作在硬件中如何实现呢？

可以利用另外的一个加法器将X取反之后加1,或者就直接使用图中的加法器将X取反之后加1，将其暂存在A中，下一次再把它放入到X中，A中存放被减数，然后进行实际的减法运算，这是这样运算非常的麻烦。在计算中进行加法器实现的时候不会采用这种方式。在数字逻辑电路中，设计全加器的时候，每一位全加器实际上有三个输入，有两个输入对应了加法的相应位，还有一个输入是后面送上来的进位，那我们对X中数进行求补运算的话，每位取反很容易，只需要在加法器和X寄存器中增加一个反向器，就可以解决取反操作，末位加1通过低位送来的进位，我们将其置1来实现末位加1的操作。

（三）乘法运算

1、 分析笔算乘法
如：A = - 0.1101 B = 0.1011，计算A * B，笔算过程如下：

得到： A * B = - 0.10001111

根据上面的笔算过程得出如下结论：

（1）数值是通过乘法计算求得，符号心算求得。在计算机中，我们可以使用异或电路求得。

（2）乘数的某一位决定是否加被乘数，为1，加上被乘数，为0，加0，相当于不加。在计算机中，可以将乘数放于一个移位寄存器中，每次取最低位1还是0判断是否加被乘数，判断完之后将乘数右移，下次继续取最低位判断。

（3）将四个位积进行累加。在计算机中，经过多次移位累加即可。如，将第一个位积放于寄存器中，和第二个位积相加，从上图中可看出，再进行相加的时候之前，需要将第二个寄存器中位积的值左移一位。实际上可以进行这样的操作：被乘数的位置不动，位积每次相加的时候进行右移一位，来替代被乘数的左移一位，这样通过四个移位和四个加法就能够得到结果。

（4）乘法的结果，数值位数扩大了一倍。在计算机中，采用两个寄存器保存结果数据即可。

2、改进笔算乘法

上图中，整个计算过程中，保持被乘数A不变，通过在当前位积每次和下一个位积相加之前把当前的位积进行右移一位（如上图中的第2步），来实现被乘数A的左移。由于上面的计算推理过程都是二进制，所以0.1=2^-1。对上面的改进结果进行细致的分析如下：下图中的8个步骤和上图中一一对应。

对于上面表格中的分析可得：

（1）乘法操作可以通过加法和移位实现，n = 4时，加四次，移位四次，n是参加运算的数据的数值部分，

（2）由乘数的末位决定被乘数是否与原部分积相加， 然后右移1位形成新的部分积，同时乘数右移1位 （末位移丢），空出高位存放部分积的低位。

（3）被乘数只与部分积的高位相加 。实际运算过程中，将被乘数放于 X寄存器中，乘数放于乘商（MQ）寄存器中，乘法累加值的高位放于ACC寄存器，ACC寄存器的值数值部分的长度进行右移过程中，低位被移入MQ寄存器中，MQ寄存器中保存的乘数也在进行逐渐右移，每次会把已经用过的最低位移位丢掉，根据新的最低位判断是否需要加上被乘数。另外被乘数只是和部分积的高位相加。 也就是被乘数只和ACC中保存的部分积高位相加，不和MQ中保存的部分积的低位相加。

（4）从硬件上说，我们需要三个寄存器，和一个全加器。一个寄存器用于保存被乘数，因为被乘数一直需要和部分积相加，所以被乘数一直需要保存。ACC用于保存部分积的高位，MQ用于保存乘数和部分积的低位。所以三个寄存器中，X寄存器不需要有移位功能，但是ACC和MQ寄存器需要有移位功能。全加器用于部分积和被乘数相加的实现，这个全加器需要n+1位，因为加法操作加的是高位部分。

3、原码乘法
原码一位乘运算规则如下，以小数为例：

对于上面的运算：
1、 乘积的符号位单独处理（两个数的符号位异或运算）
2、 数值部分为绝对值相乘。

原码一位乘递推公式如下，这个和前面笔算改进中的递推类似。

举例：


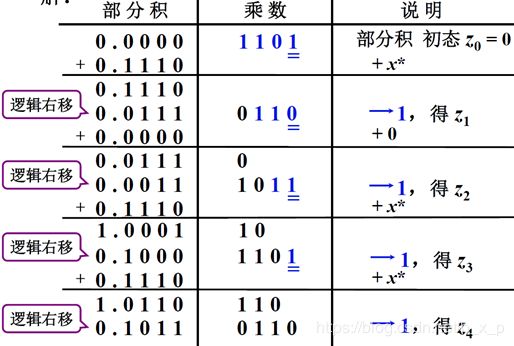
乘法过程中，因为运算采用的是绝对值运算，所以右移操作采用的是逻辑右移，将符号位和数值位同时进行右移，左边空出来的部分补0.经过一系列操作得到结果如下：

得出原码一位乘法特点：

1、 绝对值运算。

2、 移位采用逻辑移位，看似是符号位的位置，表示的是数值并非符号。

3、 使用移位次数判断移位是否结束。原码乘法，如果数值部分是n位的话，我们经过n次的加法，每次加法之后都有一次移位，所以是n此加法，n次移位。所以移位次数和数值长度有关，和机器字长有关。

原码一位乘法硬件配置：

ACC，X，MQ均为n+1位的。

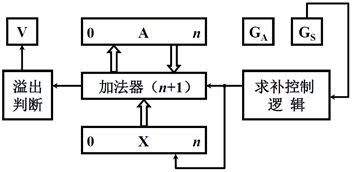
ACC：ACC寄存器公有n+1位，其中最高位实际上并不是符号位，他保存的是低位数值部分相加以后向高位的进位。

X：X寄存器保存被乘数，计算过程中，被乘数的值保持不变。

MQ：乘商寄存器，计算刚刚开始的时候，里面保存的是乘数的数值，随着计算过程的进行，一边计算一边进行移位，他的高位部分逐渐被累加和的低位部分占据，乘数的低位部分每次移位都会移丢最低位，直到完成n次移位，所以的乘数的数值位部分都被移丢，运算就结束了。

计算器C：用来记录移位的次数，数值部分是n，移位的次数就是n，每移位一次给计数器减一，当计数器为0的时候，运算过程就结束了。

S：符号位，把参加运算的两个数的符号位进行异或，将结果赋值给S。

GM：乘法标识。

移位和加控制：移位控制和加法控制，做一次加法，做一次移位，加法和移位由乘数的最低位进行控制。

控制门：运算过程中，当乘数的最低位为1的时候，控制门打开，将X中的被乘数送入加法器和A中的数据进行累加。当乘数的最低位为0的时候，控制门直接将0送入到加法器和A中的数据进行累加，或者，当不往累加器中送入0，直接由移位和加控制完成移位操作，说到这里大家就能理解，为什么上面说的是使用移位的次数控制乘法的结束而不是通过加法的次数控制移位的结束，移位加0可以不做加法直接做移位操作，移位操作的次数是不会有变化的。

4、补码乘法
补码一位乘运算规则如下，以小数为例：

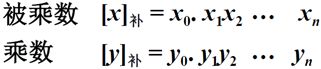
（1）被乘数任意，乘数为正。
与原码乘相似，但加和移位按补码规则运算（算术移位）。乘积的符号自然形成，不需要和原码乘法一样单独异或操作形成。
[X * Y]补 = [X ]补 * [Y]补 = [X ]补 * 0.y1y2…yn，成立条件是Y0 = 0

（2）被乘数任意，乘数为负。
乘数[y]补，去掉符号位，然后操作同 ①，最后 加[–x]补，校正
[X * Y]补 = [X ]补 * 0.y1y2…yn + [–x]补，成立条件 Y0 = 1

如果使用上面两个方式结合计算补码乘法，会导致硬件设计复杂。

（3）Booth 算法 （被乘数、乘数符号任意）

对1和2中的计算公式进行处理得：

在计算机中进行补码运算，A + [-X]补 == A - [X]补。
对上面得到的公式进行变化处理：

这样的到的乘法和原码乘法就非常的类似。
从上面的推导过程得到Booth 算法递推公式如下：

计算过程中如何实现上面递推公式中的：

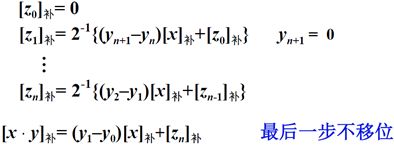
在具体实现中，采用一个译码器，将Yi+1 和 Yi作为译码器的输入，输出四种信号，分别是：00,01,10,11。对不同的信号进行不同的操作，具体如下：

在Booth 算法乘法中，符号位要参加运算。
对于Booth 算法，举例：


上图中，第一步中，乘数末尾的0属于推中的附加位Yn+1。计算过程中符号位参与运算，会溢出，所以采用的是两位符号位。

Booth 算法的硬件配置：

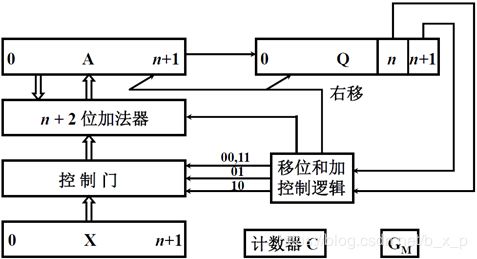
ACC、X、MQ 均 n + 2 位，因为计算过程中使用的是双符号位计算。乘数计算时候的是单符号位，但是计算最开始给乘数增加了一位附加位。

ACC：最初始存放的是0，存放的是部分积和最终结果的高位部分。

MQ：存放乘数和最终结果的低位部分。

X：保存被乘数。

移位和加控制逻辑：输入Yi+1 和 Yi，输出四种信号控制逻辑门，加法器和移位操作。

乘法总结：
1、 整数乘法与小数乘法过程完全相同 ，可用 逗号 代替小数点
2、 原码乘 符号位 单独处理
补码乘 符号位 自然形成
3、 原码乘去掉符号位运算，即为无符号数乘法
4、 不同的乘法运算需有不同的硬件支持

（四）除法运算

1、分析笔算除法

上面计算步骤如下：

1、 被除数X小于除数Y，所以上商0，上商结束后，把被除数后面添加0，然后和右移一位的除数组比较。

2、 右移一位的除数是0.01101，小于加了0以后的被除数，所以上商1，上商结束后，减掉右移一位的除数得到新的余数。然后再产生的余数后面添加0，和右移两位的除数作比较。

3、 右移两位的除数，小于添加0以后的余数，所以上商1，上商结束后，减掉右移两位的除数得到新的余数。然后再产生的余数后面添加0，和右移三位的除数作比较。

4、 右移三位的除数，大于添加0以后的余数，所以上商0。继续给新的余数添加0，再和右移四位的除数进行比较。

5、 右移四位的除数，小于添加0以后的余数，所以上商1，然后再做减法得到最终的余数。到此不在继续上商原因是寄存器容量有限，商值已经占用了寄存器所有空间。

得到如下结果：

对于上面笔算的过程得：

1、 商符单独处理，在计算机中很容易实现，只需要一个异或电路即可。

2、 心算上商：除数小于余数，所以上商1，除数大于余数，所以上商0。

3、 余数不动，低位补0，减去右移一位的除数，在整个除法过程中，除数一直被移位。上面的计算过程中，上了五次商，做了四次移位。计算过程中余数的位数越来越多，除数被不停的进行右移，数值位的长度由四位变成了8位，所以原来我们是使用的是n位的加法器来完成减法操作，现在n位加法器无法完成加法的操作，所以要使用2n位的加法器。

4、 上商位置不固定。上商数量和机器字长相等时结束运算。

2、笔算除法和机器除法的比较：

对于上面的比较结果：
1、在机器中，上商0还是上商1，通过余数和除数之间的差值结果进行判断。
2、笔算中给余数末尾添加0减右移除数操作中，移位操作是相对的，所以在机器中，可以采用左移一位余数低位补0减除数进行实现。
3、根据2中的将余数左移低位补0，所以只需要一倍长的加法器就可以实现余数和被除数的减法操作。
4、在机器中，上商位置可以进行固定，从MQ寄存器的低位进行上商，每次上商将MQ中的商进行左移

2、原码除法，以小数为例

计算过程中约定：
1、小数定点除法中：X绝对值 < Y绝对值，因为小数定点机中只能保存小数，结果也必须是小数。
2、整数定点除法中：X绝对值 > Y绝对值，因为整数定点机中只能保存整数，结果也必须是整数。
3、除数不能为0，除数为0，直接通过判0电路给出结果为0
4、被除数不能为0，为0将会出现异常操作。

（1）恢复余数法

如，以此为例：

在这个例子中，假设机器数5位，符号位占用1位，在小数定点机中进行计算。在计算过程中，上商操作要判断余数减除数的结果，在计算机中通过余数加上除数的补码进行完成。

整个计算过程如下：

对于上图中的红色步骤具体说明如下：
1、 最开始，商为0.
2、 将被除数（余数）和除数进行比较（+[-Y]补）
3、 减法结果为1.1110说明不够减，所以上商0.
4、 因为上商上的是0不是1，所以这个减法操作做的不对，需要恢复减掉除数的余数（+[Y]补）。恢复后余数的值和原来的被除数完全相同。
5、 把余数左移一位，这里采用的是逻辑左移。
6、 对移位后的余数做减法操作。
7、 减法结果得到0.1001，所以上商1，所以减法是对的，余数的值是真正的余数。
8、 把余数左移一位。
9、 对移位后的余数做减法操作。
10、 减法得到正值，上商1.
11、 把余数左移一位。
12、 对移位后的余数做减法操作。
13、 余数为负，上商0，
14、 恢复余数。
15、 把余数左移一位。
16、 对移位后的余数做减法操作。
17、 结果为正，上商1

上面计算结果：

整个计算过程中：
1、上商五次，进行了四次移位。第一次上商后要判断是否发生溢出，在小数定点机中，如果第一次上商为1，表明发生了溢出，因为在小数定点机中只能表数绝对值小于1的数。
2、余数为正上商1，余数为负上商0(上商0时需要恢复余数)
3、因为假设机器数5位，所以上商五次后就终止运算。

（2）不恢复余数法：

在恢复余数法中，每次上商0和上商1后，接下来判断下次上商0还是上商1的操作如下：

对于上面的规则：
1、2R表示将余数左移一位。
2、余数 > 0，上商1，根据2R – Y判断下次上商0还是上商1.
余数 < 0, 先恢复余数，然后减Y判断上商0还是上商1，其中恢复余数和减Y操作进行结合，结果就如图中红色框中所示。所以对于这种判断上商方式我们称为不恢复余数法。

不恢复余数法采用如下规则：也称为加减交替法

下面举例说明加减交替法的上商过程，以下为例：

计算上商过程如下：

对上上图中的计算步骤说明如下：
1、 商值初始值为0
2、 做减法操作，因为此时还未上商，没办法根据上商结果判断只用那种规则。所以首先要先判断是否发生溢出，第一位应该上什么样的商。
3、 减法小于0，所以上商0
4、 根据上商为0，根据规则，将余数左移1位然后加上[Y]补
5、 得到结果大于0，上商1.
6、 根据上商为1，根据规则，将余数左移1位然后加上[-Y]补
7、 得到结果大于0，上商1
8、 根据上商为1，根据规则，将余数左移1位然后加上[-Y]补
9、 减法小于0，所以上商0
10、 根据上商为0，根据规则，将余数左移1位然后加上[Y]补
11、 得到结果大于0，上商1

运算结束。得到结果：

对于计算过程：
若数值位为n位，
1、上商n+1次。
2、第一次上商判断溢出。
3、移位n次，加n+1次，每次上商都会进行加法操作。
4、采用移位的次数判断除法是否结束。

减交替除法硬件配置如下：

ACC：用于保存被除数和余数

X：用于保存除数

MQ：保存商，

移位和控制逻辑：通过MQ中的第n位上商的结果判断，A中的余数左移一位后加上X中[除数]补还是加上[- 除数]补，即判断加法器做加法操作还是做减法操作。

C：计数器，在加减交替法除法中，做了n次移位，n + 1次加法，通过移位或者加法次数作为除法操作停止控制。

GD：除法标志。

S：符号位

V：是否发生溢出

A，X，Q都是n+1位的，一位符号位，n位数值位。

浮点加减法运算

浮点计算中，设X， Y的值如下：

两个浮点数如果要进行加减法运算，他们的阶码（或者是指数）必须是相同的，尾数的基值可能是2,4,8,16….，本文中设尾数的基值为2.，如果尾数的基值相同的情况下，阶码的值是不同的，那我们就需要对阶码的值进行调整，而且调整同时，尾数的值也要进行调整，通过阶码和尾数两部分的调整，保证参与运算的数据他的值的大小不发生变化，依然等于原始参加运算的值，从而保证加减法结果的正确性。

（一）对阶

求阶差，计算机中通过补码的加法运算实现减法运算，求阶差 同样使用补码运算。

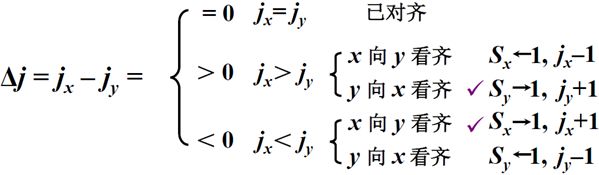
在阶码对齐，当阶码存在不齐的情况时，对齐方式分别有两种，但其中左移尾数减小阶码的方式可能造成位数高位部分的1被移丢，，从而造成数据错误，所以尾数左移是不合适的。在右移尾数增加阶码的方式中，虽然右移尾数会导致低位数据丢失，但低位数据丢失只会影响数据的精度，不会影响数据的大小，所以在计算机中，采用右移尾数增加阶码的方式，即小阶向大阶看齐。

举例如下：

求解过程如下：

（二）尾数求和

上面计算得到的数并不是一个规格化的数据，所以接下来需要对计算结果进行规格化。

（三）浮点数规格化

规格化数的定义如下：

1、规格化数的判断

在实际情况中判断规格化数的方式如下：

根据上面的判断方式可以得出下面的结论：

在实际情况中，我们判断规格化数实际上采用的就是上面这种方式，而不是完全采用规格化数的定义。因为对于补码有两个特例：

特例1：

特例2：

对于上面这两种特例，就不能使用补码的定义进行判断。

2、对数据进行规格化方式：

（1）左规
将尾数进行左移，使得尾数规格化。

举例，对于数据：

左规后结果如下：

（2）右规

将尾数进行右移，使得尾数规格化。
在补码计算过程中，采用双符号位进行计算，如果计算的结果符号位两位不同，说明计算产生了溢出，此时需要进行右规操作。即：

对于上面的浮点数的加减法计算过程，举例如下：

因为是补码操作，所以不管是阶码还是尾数，他们的符号位都取两位。

首先计算出x， y的补码：

对阶：

尾数求和：

得到结果如下：

对计算结果进行右规：

（四）舍入

舍入指数据长度超过了计算机中存储数据的物理器件能够保存数据的长度，低位部分要进行处理，保证数据能比较精确的保存在计算机中，在对阶和右规过程中，尾数都可能会向右进行移动 ，低位部分就会丢失造成误差，为了尽可能的减小误差，我们要进行舍入操作，舍入的方法有：

1、截断：移除去的数据直接扔掉。
2、0舍1入，和四舍五入类似，如果被丢掉的数据是1，就在可保存的这个数据的最低位加1.
3、末位恒置1法：不管后面被丢掉的数据是什么，保存在计算机中的数据的最低位都是1。

举例如下：

计算过程依旧采用补码进行计算，采用双符号位，这样在判断结果的溢出情况时比较容易。

计算x， y的补码：

对阶：

尾数求和：

得到计算结果如下：

对计算结果进行右规：

（五）溢出判断

这里说的溢出，并不是只尾数部分的溢出，右规是尾数溢出的解决方法。这里的溢出是指整个浮点数的值发生的溢出。

存放在计算机中的数据，字长是有限的，那么他表示的数的个数和表示的数据的大小都是有限的，就是在可表示的数据的范围中，表示出来的数据也都是离散的，如果数轴上某一个点没有正好落在计算机可表示数据的这个点上，那只能用近似值进行表示。


上图中，最大负数的表示中，尾数采用最小的负二分之一，由于负二分之一本身就不是规格化的数，所以对负二分之一进行规格化。

算数逻辑单元

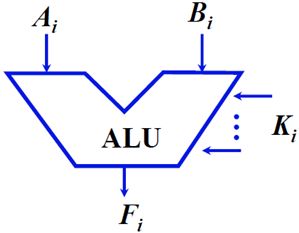
（一）ALU电路

Ai，Bi：输入，表示参加运算的数据，
Fi：结果输出，
Ki：具体做什么样的运算由Ki决定，因为算术逻辑运算单元要实现多种类型的运算和逻辑运算，需要有控制端来说明本次运算到底做的是算术运算，逻辑运算，定点运算，浮点运算中的哪一种类型的运算。

ALU电路是一个组合逻辑电路，所谓组合逻辑电路指的是没有记忆功能的，输入消失，输出端的输出结果也会消失，为了对输出端的输出结果进行保存，并且使得运算能够稳定，所以需要在输入端的Ai和Bi端连接寄存器，同时在输出端Fi也要连接寄存器，用这个寄存器保存运算结果。

（二）快速进位链

首先看一下并行加法器。

1、并行加法器

图中的并行加法器，是由n+1个全加器构成的并行加法器，之所以称之为并行加法器，是因为，两个n+1位的数可以利用这个加法器以并行的方式完成加法运算。

对于每一个全加器Fi，有三个输入，其中两个输入对应了参与运算的两个数的相应位，另外一个输入是低位的进位。有两个输出，一个输出是对应的加法和的结果对应的位，另外一个输出是本地产生的向高位的进位。

每个全加器计算结果Si是如何产生：
这个Si指出了运算结果某一位到底是1还是0。如果输入的三位都是1或者是其中只有一位是1，另外两位是0。对应的Si的值为1。表示为（加号表示或运算）：

对于上面这个表达式，涉及到了Ai, Bi, Ci-1，Ai和Bi是参与运算的两个数据，这两个数据是保存在寄存器中，对于Ai和Bi位我们在运算的时候，这个是已经知道的，随时可以参加运算，但是Ci-1是由低位产生的进位，只有这个进位产生以后，才能在这个表达式中计算出Si。所以在这个表达式中，最影响数据结果Si生成的因素就是进位，如果能够快速的产生进位，就能提高运算器的速度。

进位Ci是如何产生的：
如果三个输入都是1，或者是其中的两个输入为1，一位输入为0，就会产生进位，表示为：

对上面的表达式进行化简得：（再加两个AiBiCi-1，前三项分别和AiBiCi-1进行合并）

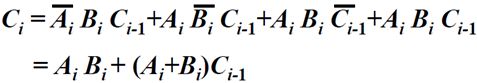
从上面可以看出，如果Ai， Bi都等于1，那Ci就等于1。或者是Ai和Bi中至少有一个为1，Ci-1才会向前进行传递。因此我们把AiBi叫做本地进位，也就是由本地参与运算的两个数据相应的位就会产生的进位，另外Ai + Bi我们用ti进行表示，表示传送条件，如果这个或的值（ti）为1，那么Ci-1的结果就会被传送到Ci，即如果Ai + Bi = 1，Ci = Ci-1。这样就可以继续对Ci化简得：

di是ai和bi的与， ti是ai和bi的或。

知道了进位是如何产生的， 那快速的产生进位，提高运算器的速度，就是进位链要完成的任务。

2、串行进位链
进位链：传送进位的电路。也就是说在加法器中，我们可以把进位的产生电路独立出来，产生进位以后相应的进位再和AiBi一起参与运算来生成Si。

串行进位链：进位的方式以串行方式向前进行传送。

以 4 位全加器为例，则每一位的进位表达式为：

为了使用与非门实现进位链，对上面的表达式根据进行变换，这个变换采用德摩根定律。以C0为例有：

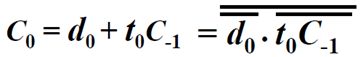
根据上面的表达式，得出如下通过与非门构成的串行进位链：每个进位的产生需要采用两个与非门。如C0产生为例：根据变换的结果，使用t0和C-1的与操作，再做非操作输出，之后用d0的非和之前得到的结果再做与操作，非操作，就可以得到C0。C1，C2，C3同理。

设与非门的级延迟时间为ty，则有：

3、并行进位链

并行进位链，让N位加法器的进位同时产生。
以四位加法器为例：

首先对串行进位链中得到的表达式再进行转换得到：

利用上面得到的表达式提高进位产生的速度，虽然这些逻辑表达式有很多项，但是都是与操作或操作，如果我们使用与门或门，经过两级门，我们就可以计算出每一个Ci。通过与或非门实现电路如下：

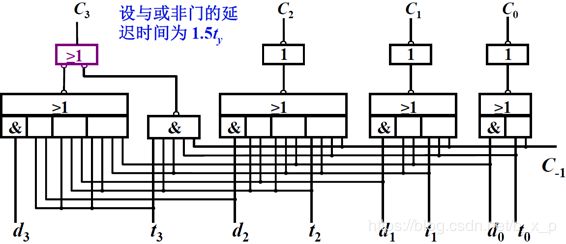
通过上面的电路，我们就可以实现n位加法器进位同时产生；

设与或非们的延迟时间为1.5ty，则有：

那么上面这种方式我们称之为现行进位或者是跳跃进位。

那么跳跃进位他的电路比较复杂，每个门的擅入都比较大，现在只有四位参与运算，如果是32为产生进位，同时产生进位，那么这个电路会非常复杂。为了既然进位产生的比较快，电路的复杂程度又不太大，就给出了以下两种折中的跳跃进位链。

（1）单重分组跳跃进位链

n 位全加器分若干小组，小组中的进位同时产生， 小组与小组之间采用串行进位。

以n = 16为例：

上图中，组和组之间采用串行进位，也就是说当第四组中的C3产生以后，把C3作为输入输入到第三组中，这个C3和第三组中的di，ti配合，生成第三组中的所有Ci，同样第二组，第一组同理。

下面看一下，当di，ti形成后，通过多长时间能产生完所有的Ci：

（2）双重分组跳跃进位链

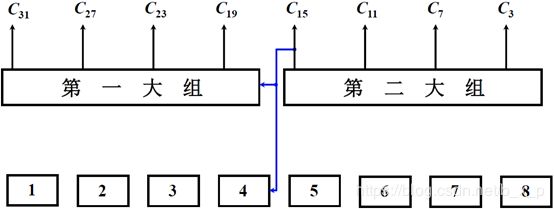
n 位全加器分若干大组，大组中又包含若干小组。每个大组中小组的最高位进位同时产生。大组与大组之间采用串行进位。

以n = 32为例：

基本思路如下：

上图中，将32为分成2个大组，每个大组中分为四个小组，每个小组中四位。C3，C7，C11，C15对应了，8，7，6，5，四个小组的最高位的进位，这四个进位同时产生。同样，对第一大组来说C19，C23，C27，C31对应了4,3,2,1四个小组中的最高位进位，这四位进位也是同事产生。另外大组和大组之间采用串行进位的方式，也就是C15产生之后，作为输入，输入到第一大组中，用以产生第一大组中每个小组的最高位的进位和其他的进位。

对大组进位分析：
首先看第八小组最高位C3的产生，计算公式如下：

同理我们可以的到第一大组中其他小组的最高位产生公式：

对上面的公式进行带入展开得到：

根据上面的分析，利用与或非门和非门，得出第二大组中每个小组最高为进位的生成电路如下：

其中每个小组中的D和T由每个小组中的输入决定，和进位无关，每个小组中D和T的产生电路如下，以第8小组为例：

此电路中只产生低三位的进位和本小组中的D，T。低三位的产生要依靠C-1，D，T的产生和C-1进位没有关系，只要有对应计算位的输入就能够产生D，T，所以只有第8组能够同时产生此电路中只产生低三位的进位和本小组中的D，T。第三位的产生要依靠C-1，D，T的产生和C-1进位没有关系，只要有对应计算位的输入就能够产生D，T，以及低三位，而其他小组当已知C-1的时候只能产生本组中的D，T，而低三位的产生要等到得到上一个小组的进位后才能产生。

再以第二大组为例，看看第二大组中整个进位产生的过程：

根据上图，当 di、 ti 和C-1形成后：

此时，只有第8小组中的低三位会产生，其他小组中的低三位不会产生，因为低三位的产生要依靠下一小组的进位。


和双重分组跳跃进位链相比：之前讲解的串行进位链和单重分组跳跃进位链当N=16时：

下面分析一下两个大组产生全部进位的时间：

当di， ti形成后：