哈夫曼编码(Huffman Coding)
霍夫曼编码(Huffman Coding)是一种编码方法,霍夫曼编码是可变字长编码(VLC)的一种。
霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
霍夫曼编码的具体步骤如下:
1)将信源符号的概率按减小的顺序排队。
2)把两个最小的概率相加,并继续这一步骤,始终将较高的概率分支放在右边,直到最后变成概率1。
3)画出由概率1处到每个信源符号的路径,顺序记下沿路径的0和1,所得就是该符号的霍夫曼码字。
4)将每对组合的左边一个指定为0,右边一个指定为1(或相反)。
例:现有一个由5个不同符号组成的30个符号的字符串:
BABACAC ADADABB CBABEBE DDABEEEBB
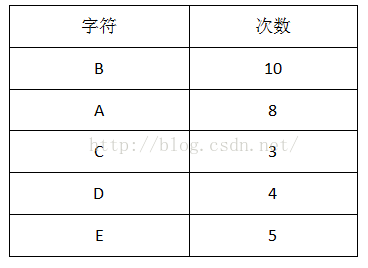
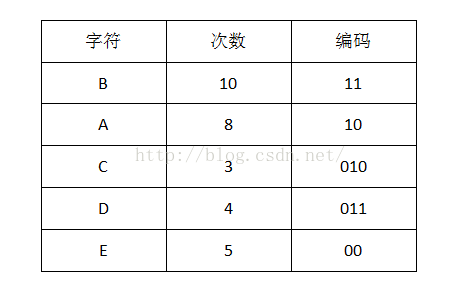
1首先计算出每个字符出现的次数(概率):
2把出现次数(概率)最小的两个相加,并作为左右子树,重复此过程,直到概率值为1
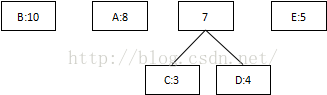
第一次:将概率最低值3和4相加,组合成7:
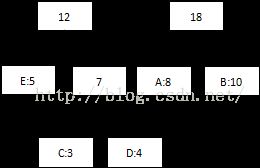
第二次:将最低值5和7相加,组合成12:
第三次:将8和10相加,组合成18:
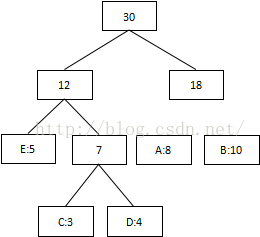
第四次:将最低值12和18相加,结束组合:
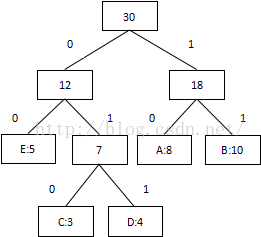
3 将每个二叉树的左边指定为0,右边指定为1
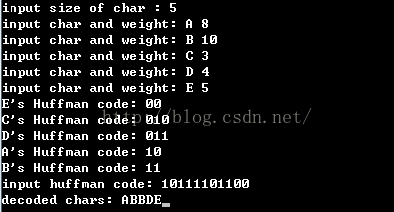
4 沿二叉树顶部到每个字符路径,获得每个符号的编码我们可以看到出现次数(概率)越多的会越在上层,编码也越短,出现频率越少的就越在下层,编码也越长。当我们编码的时候,我们是按“bit”来编码的,解码也是通过bit来完成,如果我们有这样的bitset “10111101100″ 那么其解码后就是 “ABBDE”。所以,我们需要通过这个二叉树建立我们Huffman编码和解码的字典表。
这里需要注意的是,Huffman编码使得每一个字符的编码都与另一个字符编码的前一部分不同,不会出现像’A’:00, ’B’:001,这样的情况,解码也不会出现冲突。
霍夫曼编码的局限性
利用霍夫曼编码,每个符号的编码长度只能为整数,所以如果源符号集的概率分布不是2负n次方的形式,则无法达到熵极限;输入符号数受限于可实现的码表尺寸;译码复杂;需要实现知道输入符号集的概率分布;没有错误保护功能。
霍夫曼编码实现 (C++实现):
-
int main()
-
{
-
int n, w;
-
char c;
-
string s;
-
-
cout <<
"input size of char : ";
-
cin >> n;
-
BinartNodes bn;
-
for(
int i =
0; i != n; ++i)
-
{
-
cout <<
"input char and weight: ";
-
cin >> c >> w;
-
bn.add_Node((Node(c, w)));
-
cin.clear();
-
}
-
while(bn.size() !=
1)
-
{
-
Node n1 = bn.pop(),
//获取前两个权重最小的结点
-
n2 = bn.pop();
-
Node h(' ', n1.get_weight() + n2.get_weight());
//新建结点,权重为前两个结点权重和
-
if( n1.get_weight() < n2.get_weight())
//权重较小的结点在新结点左边
-
{
-
h.
set(n1, n2);
//设置新结点左右子结点
-
}
-
else
-
{
-
h.
set(n2, n1);
-
}
-
bn.add_Node(h);
//将新结点插入到multiset中
-
}
-
encodeing(bn.get_Node(), s);
//编码
-
cout <<
"input huffman code: ";
-
cin >> s;
-
cout <<
"decoded chars: ";
-
decoding(bn.get_Node(), s);
//解码
-
}
Handle.h句柄类:
-
/*Handle.h*/
-
//句柄模型类
-
template <
class Type> class Handle{
-
public:
-
Handle(Type *ptr =
0): pn(ptr), use(
new
size_t(
1)) {}
-
Type&
operator*();
//重载操作符*
-
Type*
operator->();
//重载操作符->
-
const Type&
operator*()
const;
-
const Type*
operator->()
const;
-
Handle(
const Handle &h): pn(h.pn), use(h.use) { ++*use; }
//复制操作
-
Handle&
operator=(
const Handle &h);
//重载操作符=,赋值操作
-
~Handle() {rem_ref(); }
//析构函数
-
private:
-
Type *pn;
//对象指针
-
size_t *use;
//使用次数
-
void rem_ref()
-
{
-
if (--*use ==
0)
-
{
delete pn;
delete use; }
-
}
-
};
-
template <
class Type> inline Type& Handle
: :
operator*()
-
{
-
if (pn)
return *pn;
-
throw runtime_error(
"dereference of unbound Handle");
-
}
-
template <
class Type> inline const Type& Handle
: :
operator*()
const
-
{
-
if (pn)
return *pn;
-
throw runtime_error(
"dereference of unbound Handle");
-
}
-
template <
class Type> inline Type* Handle
: :
operator->()
-
{
-
if (pn)
return pn;
-
throw runtime_error(
"access through unbound handle");
-
}
-
template <
class Type> inline const Type* Handle
: :
operator->()
const
-
{
-
if (pn)
return pn;
-
throw runtime_error(
"access through unbound handle");
-
}
-
template <
class Type> inline Handle
& Handle: :
operator=(
const Handle &rhs)
-
{
-
++*rhs.use;
-
rem_ref();
-
pn = rhs.pn;
-
use = rhs.use;
-
return *
this;
-
}
-
/*Node.h*/
-
template <
class T> class Handle;
-
class Node{
-
friend
class Handle
;
//句柄模型类
-
public:
-
Node():ch(
’ ‘),wei(
0), bits(), lc(), rc(){}
-
Node(
const
char c,
const
int w):
-
ch(c), wei(w), bits(), lc(), rc(){}
-
Node(
const Node &n){ch = n.ch; wei = n.wei; bits = n.bits;
-
lc = n.lc; rc = n.rc; }
-
virtual Node* clone()const {
return
new Node( *
this);}
-
int get_weight() const {
return wei;}
//获取权重
-
char get_char() const {
return ch; }
//获得字符
-
Node &get_lchild() {
return *lc; }
//获得左结点
-
Node &get_rchild() {
return *rc; }
//获得右结点
-
void set(const Node &l, const Node &r){
//设置左右结点
-
lc = Handle
(
new Node(l));
-
rc = Handle
(
new Node(r));}
-
void set_bits(const string &s){bits = s; }
//设置编码
-
private:
-
char ch;
//字符
-
int wei;
//权重
-
string bits;
//编码
-
Handle
lc;
//左结点句柄
-
Handle
rc;
//右结点句柄
-
};
-
inline bool compare(const Node &lhs, const Node &rhs);
//multiset比较函数
-
inline bool compare(const Node &lhs, const Node &rhs)
-
{
-
return lhs.get_weight() < rhs.get_weight();
-
}
-
class BinartNodes{
-
typedef bool (*Comp)(const Node&, const Node&);
-
public:
-
BinartNodes():ms(compare) {}
//初始化ms的比较函数
-
void add_Node(Node &n){ms.insert(n); }
//增加Node结点
-
Node pop();
//出结点
-
size_t size(){
return ms.size(); }
//获取multiset大小
-
Node get_Node() {
return *ms.begin();}
//获取multiset第一个数据
-
private:
-
multiset
ms;
-
};
-
/*Node.cpp*/
-
#include “Node.h”
-
Node BinartNodes::pop()
-
{
-
Node n = *ms.begin();
//获取multiset第一个数据
-
ms.erase(ms.find(*ms.begin()));
//从multiset中删除该数据
-
return n;
-
}
![]()
霍夫曼编码实现 (C语言实现):
-
#include
-
#include
-
#include
-
#include
-
-
#define MAXBIT 100
-
#define MAXVALUE 10000
-
#define MAXLEAF 30
-
#define MAXNODE MAXLEAF*2 -1
-
-
typedef
struct
-
{
-
int bit[MAXBIT];
-
int start;
-
} HCodeType;
/* 编码结构体 */
-
typedef
struct
-
{
-
int weight;
-
int parent;
-
int lchild;
-
int rchild;
-
char value;
-
} HNodeType;
/* 结点结构体 */
-
-
/* 构造一颗哈夫曼树 */
-
void HuffmanTree (HNodeType HuffNode[MAXNODE], int n)
-
{
-
/* i、j: 循环变量,m1、m2:构造哈夫曼树不同过程中两个最小权值结点的权值,
-
x1、x2:构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/
-
int i, j, m1, m2, x1, x2;
-
/* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */
-
for (i=
0; i<
2*n
-1; i++)
-
{
-
HuffNode[i].weight =
0;
//权值
-
HuffNode[i].parent =
-1;
-
HuffNode[i].lchild =
-1;
-
HuffNode[i].rchild =
-1;
-
HuffNode[i].value=
' ';
//实际值,可根据情况替换为字母
-
}
/* end for */
-
-
/* 输入 n 个叶子结点的权值 */
-
for (i=
0; i
-
{
-
printf (
"Please input char of leaf node: ", i);
-
scanf (
"%c",&HuffNode[i].value);
-
-
getchar();
-
}
/* end for */
-
for (i=
0; i
-
{
-
printf (
"Please input weight of leaf node: ", i);
-
scanf (
"%d",&HuffNode[i].weight);
-
-
getchar();
-
}
/* end for */
-
-
/* 循环构造 Huffman 树 */
-
for (i=
0; i
-1; i++)
-
{
-
m1=m2=MAXVALUE;
/* m1、m2中存放两个无父结点且结点权值最小的两个结点 */
-
x1=x2=
0;
-
/* 找出所有结点中权值最小、无父结点的两个结点,并合并之为一颗二叉树 */
-
for (j=
0; j
-
{
-
if (HuffNode[j].weight < m1 && HuffNode[j].parent==
-1)
-
{
-
m2=m1;
-
x2=x1;
-
m1=HuffNode[j].weight;
-
x1=j;
-
}
-
else
if (HuffNode[j].weight < m2 && HuffNode[j].parent==
-1)
-
{
-
m2=HuffNode[j].weight;
-
x2=j;
-
}
-
}
/* end for */
-
/* 设置找到的两个子结点 x1、x2 的父结点信息 */
-
HuffNode[x1].parent = n+i;
-
HuffNode[x2].parent = n+i;
-
HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
-
HuffNode[n+i].lchild = x1;
-
HuffNode[n+i].rchild = x2;
-
-
printf (
"x1.weight and x2.weight in round %d: %d, %d\n", i+
1, HuffNode[x1].weight, HuffNode[x2].weight);
/* 用于测试 */
-
printf (
"\n");
-
}
/* end for */
-
-
}
/* end HuffmanTree */
-
-
//解码
-
void decodeing(char string[],HNodeType Buf[],int Num)
-
{
-
int i,tmp=
0,code[
1024];
-
int m=
2*Num
-1;
-
char *nump;
-
char num[
1024];
-
for(i=
0;i<
strlen(
string);i++)
-
{
-
if(
string[i]==
'0')
-
num[i]=
0;
-
else
-
num[i]=
1;
-
}
-
i=
0;
-
nump=&num[
0];
-
-
while(nump<(&num[
strlen(
string)]))
-
{tmp=m
-1;
-
while((Buf[tmp].lchild!=
-1)&&(Buf[tmp].rchild!=
-1))
-
{
-
if(*nump==
0)
-
{
-
tmp=Buf[tmp].lchild ;
-
}
-
else tmp=Buf[tmp].rchild;
-
nump++;
-
-
}
-
printf(
"%c",Buf[tmp].value);
-
}
-
}
-
-
int main(void)
-
{
-
-
HNodeType HuffNode[MAXNODE];
/* 定义一个结点结构体数组 */
-
HCodeType HuffCode[MAXLEAF], cd;
/* 定义一个编码结构体数组, 同时定义一个临时变量来存放求解编码时的信息 */
-
int i, j, c, p, n;
-
char pp[
100];
-
printf (
"Please input n:\n");
-
scanf (
"%d", &n);
-
HuffmanTree (HuffNode, n);
-
-
for (i=
0; i < n; i++)
-
{
-
cd.start = n
-1;
-
c = i;
-
p = HuffNode[c].parent;
-
while (p !=
-1)
/* 父结点存在 */
-
{
-
if (HuffNode[p].lchild == c)
-
cd.bit[cd.start] =
0;
-
else
-
cd.bit[cd.start] =
1;
-
cd.start--;
/* 求编码的低一位 */
-
c=p;
-
p=HuffNode[c].parent;
/* 设置下一循环条件 */
-
}
/* end while */
-
-
/* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */
-
for (j=cd.start+
1; j
-
{ HuffCode[i].bit[j] = cd.bit[j];}
-
HuffCode[i].start = cd.start;
-
}
/* end for */
-
-
/* 输出已保存好的所有存在编码的哈夫曼编码 */
-
for (i=
0; i
-
{
-
printf (
"%d 's Huffman code is: ", i);
-
for (j=HuffCode[i].start+
1; j < n; j++)
-
{
-
printf (
"%d", HuffCode[i].bit[j]);
-
}
-
printf(
" start:%d",HuffCode[i].start);
-
-
printf (
"\n");
-
-
}
-
printf(
"Decoding?Please Enter code:\n");
-
scanf(
"%s",&pp);
-
decodeing(pp,HuffNode,n);
-
getchar();
-
return
0;
-
}
转载自:“https://blog.csdn.net/xgf415/article/details/52628073”