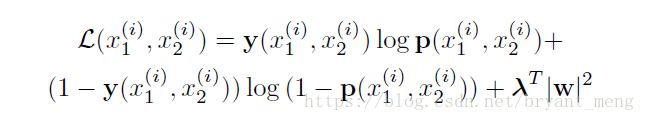【One Shot】《Siamese Neural Networks for One-shot Image Recognition》

ICML-2015

---

---

1 Motivation

  机器学习虽然在很多领域取得不错的结果，但是 It often broken down when forced to make predictions about data for which little supervised information is available.

  李飞飞第一次提出One-short learning的概念
  One-shot learning may only observe a single example of each possible class before making a prediction about a test instance.

  但是One-shot learning excel at similar instances but fail to offer robust solutions that may be applied to other types of problems.

  作者基于One-shot learning的方法，结合了siamese neural networks，通过学习discriminative来改善传统机器学习的这种缺陷！

2 Innovation

  我觉得是one-shot 和 Siamese Neural Networks的一种结合（用了深度的网络）

3 Advantages

  1） are capable of learning generic image features useful for making predictions about unknown class distributions，哪怕未知类样本很少

  2）很容易训练

  3）用深度学习的方法，而不是 rely domain-specific knowledge

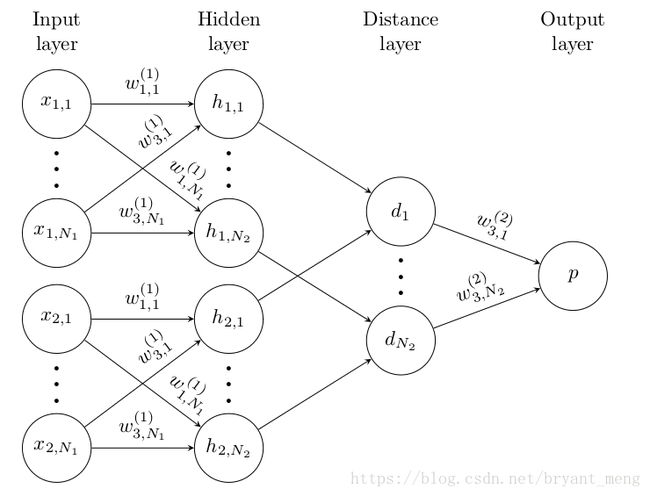
4 Model

$L$ layers each with $N_l$ units
$h_{1,l}$ denotes layer $l$ for the first twin
$h_{2,l}$ denotes layer $l$ for the second twin

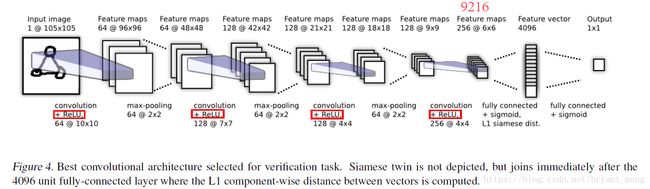
  Thus the kth filter map in each layer takes the following form

  卷积→ReLU→max pooling

  单个网络，没有画出孪生网络，孪生网络实际是这样的

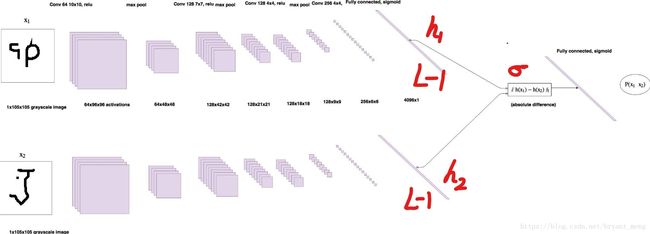
  最后的连接方式为
$$p=\sigma (\sum _j{\alpha }_j\left|h_{1,L-1}^{(j)}-h_{2,L-1}^{(j)}\right|)$$

  The ${\alpha }_j$ are additional parameters that are learned by the model during training.

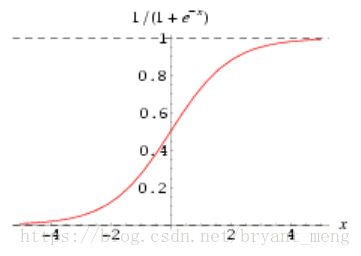
  $ \sigma$ 是sigmoid函数，图形如下 $1/(1+e^{-x})$

4 Learning

4.1 loss function

  采用的是cross entropy 损失

  $y$ 是 label，如果 $x_1$，$x_2$ 是同一类，则 $y(x_1,x_2)$为1，否则为 0
  $\lambda {\left|W\right|}^2$ 是正则化

  我们可以验证下上面的损失函数
  1）当$x_1$，$x_2$ 是同一类
  $y(x_1,x_2)$为1，$1-y(x_{1},x_{2}) 为 0 $，$L(x_{1},x_{2}) = log p(x_{1},x_{2}) $，要使得 $L(x_{1},x_{2}) $更小，则 $ p(x_{1},x_{2})$更小，根据 $p$ 的定义知，$h_{1,L-1}^{(j)}，h_{2,L-1}^{(j)}$需要差距更小，与假设$x_1$，$x_2$ 是同一类相吻合。

  2）当$x_1$，$x_2$ 不是同一类
  $y(x_1,x_2)$为0，$1-y(x_{1},x_{2}) 为 1 $，$L(x_{1},x_{2}) = log (1-p(x_{1},x_{2})) $，要使得 $L(x_{1},x_{2}) $更小，则 $ p(x_{1},x_{2})$更大，根据 $p$ 的定义知，$h_{1,L-1}^{(j)}，h_{2,L-1}^{(j)}$需要差距更大，与假设$x_1$，$x_2$ 不是同一类相吻合。

4.2 Optimization

  采用mini-batch size、momentum、learning rate、regularization 策略优化，公式如下

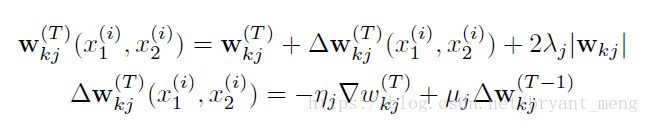
  $▽W_{kj}$ is the partial derivative with respect to the weight between the $j$ th neuron in some layer and the $k$ th neuron in the successive layer.

  $M$ - mini-batch is 128

  $i$ - $i$th mini-batch

  $\eta$ - learning rate

  $\mu$ - momentum

  $\lambda $ - regularization

  $T$ - epoch

4.3 Weight initialization

  卷积层的 W 初始化满足正态分布，zero-mean、standard deviation 0.01
  卷积层的 b 初始化满足正态分布，mean 0.5 、 standard deviation 0.01

  全连接层 W 初始化满足正态分布，zero-mean、standard deviation 0.2
  全连接层的 b 初始化和卷积层的一样

4.4 Learning schedule

  ${\eta }^T=0.99{\eta }^{T-1}$ learning rate 随着 epoch 在衰减

  $\mu$ momentum 初始化0.5，最终到 ${\mu }_j$，随着epoch线性增长

  epoch 为 200，作者在validation上随机选出 a set of 320 one shot learning tasks用于监控，20 epochs没有下降的话就停止训练，选最优表现的参数。loss一直下降的话就不停止。

4.5 Hyperparameter optimization

  用Bayesian optimization framework，在
  $\eta \in [10^{-4},10^{-1}]$
  $\mu \in [0,1]$
  $\lambda \in [0,0.1]$
  卷积核 3×3 到 20×20
  卷积核个数 从16 to 256 using multiples of 16
  Fully-connected layers ranged from 128 to 4096 units
  选最优的

4.6 Affine distortions

  仿射变换
  $T=(\theta ,{\rho }_x,{\rho }_y,s_x,s_y,t_x,t_x)$

  $\theta \in [-10.0,10.0]$

  ${\rho }_x,{\rho }_y\in [-0.3,0.3]$

  $s_x,s_y\in [0.8,1.2]$

  $t_x,t_x\in [-2,2]$

  Each of these components of the transformation is included with probability 0.5.

  仿射变换的原理可以看这篇博客 affine transformation matrix 仿射变换矩阵 与 OpenGL

5 Training and Testing

5.1 Database

  Omniglot consists of 1623 characters from 50 different alphabets. Each of these was hand drawn by 20 different people.

  在Omniglot data set上，此数据集有
  50 种 alphabets（语言）
  每种 alphabets 有15 to upwards of 40 characters（字符）
  每种characters 有 20个drawers（样本）

  40 种 alphabet 作为 background set（train）
  10 种 alphabet 作为 evaluation set（test）

  The background set is used for developing a model by learning hyperparameters and feature mappings.

  The evaluation set is used only to measure the one-shot classification performance.

5.2 Training

  比如mini-batch是32，就一次输入32组图片，从训练集中的 characters 中随机选32种（比如训练集有1200种characters），记为 categories[0-31]

  1-16组的label为0，17-32组的label为1

5.3 Testing

  N-way，比如20-way，从测试集中选20种 characters，记录为category[0-19]

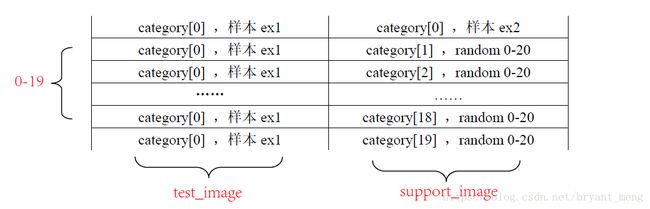
  这只是对一个图片做了测试，循环 k 次，相当于测试了 k 张图

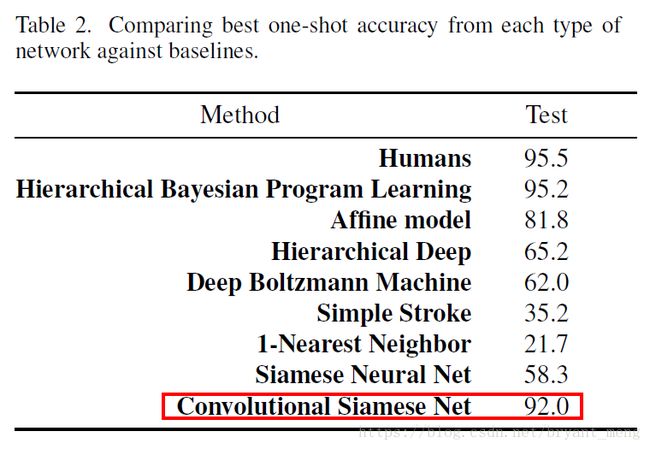
6 Experiment

  下面是一些方法的对比，横坐标是N-way

  代码地址 https://github.com/sorenbouma/keras-oneshot
  代码作者对论文的解析 https://sorenbouma.github.io/blog/oneshot/
  翻译版本 http://www.sohu.com/a/169212370_473283

---

参考
【1】One Shot Learning and Siamese Networks in Keras
【2】affine transformation matrix 仿射变换矩阵 与 OpenGL
【3】https://github.com/sorenbouma/keras-oneshot
【4】https://github.com/Goldesel23/Siamese-Networks-for-One-Shot-Learning
【5】【深度神经网络 One-shot Learning】孪生网络少样本精准分类
【6】当小样本遇上机器学习 fewshot learning
【7】深度学习: Zero-shot Learning / One-shot Learning / Few-shot Learning
【8】《Matching Networks for One Shot Learning》