【Keras-CNN】MNIST
文章目录
- 1 Data preprocessing
- 2 Build Model
- 2.1 Cross-correlation VS Convolution(★★★★★)
- 2.2 Max-pooling
- 2.3 参数量计算
- 3 Training process
- 4 可视化训练过程
- 5 评估模型的precision
- 6 Predict
- 7 可视化预测结果
- 8 Confusion Matrix
连载系列《TensorFlow+Keras》Learning notes
本文用 Convolutional Neural Network(CNN)进行MNIST识别,CNN由Yann LeCun 提出,与MLP的区别在于,前面用卷积进行了特征提取,后面全连接层和Multilayer Perceptron(MLP)一样,MLP的demo可以查看这篇博客【Keras-MLP】MNIST,本文的套路都是基于这篇博客的
1 Data preprocessing
from keras.datasets import mnist
from keras.utils import np_utils
import numpy as np
np.random.seed(10)
(x_Train, y_Train), (x_Test, y_Test) = mnist.load_data()#载入数据集,没有的话会下载
x_Train4D=x_Train.reshape(x_Train.shape[0],28,28,1).astype('float32')# 60000,28,28,1
x_Test4D=x_Test.reshape(x_Test.shape[0],28,28,1).astype('float32')#10000,28,28,1
# 归一化
x_Train4D_normalize = x_Train4D / 255
x_Test4D_normalize = x_Test4D / 255
# one-hot Encoding
y_TrainOneHot = np_utils.to_categorical(y_Train)
y_TestOneHot = np_utils.to_categorical(y_Test)
Output
Using TensorFlow backend.
归一化(标准化)的目的,提高模型预测的准确率,并且收敛更快
2 Build Model
from keras.models import Sequential
from keras.layers import Dense,Dropout,Flatten,Conv2D,MaxPooling2D
# 蛋糕架子
model = Sequential()
# 加蛋糕
# 卷积层1,输入28,28 输出 28,28
model.add(Conv2D(filters=16,
kernel_size=(5,5),
padding='same',
input_shape=(28,28,1),
activation='relu'))
# 池化层1,输入图片28,28 输出14,14
model.add(MaxPooling2D(pool_size=(2, 2)))
# 卷积层2,输入图片14,14 输出 14,14
model.add(Conv2D(filters=36,
kernel_size=(5,5),
padding='same',
activation='relu'))
# 池化层2,输入图片14,14 输出7,7
model.add(MaxPooling2D(pool_size=(2, 2)))
# 加入dropout,丢25%
model.add(Dropout(0.25))
# 36*7*7 转化为一维向量,1764个float
model.add(Flatten())
# 全连接,128
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
# output layer
model.add(Dense(10,activation='softmax'))
print(model.summary())
Output
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 28, 28, 16) 416
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 14, 14, 16) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 14, 14, 36) 14436
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 7, 7, 36) 0
_________________________________________________________________
dropout_1 (Dropout) (None, 7, 7, 36) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 1764) 0
_________________________________________________________________
dense_1 (Dense) (None, 128) 225920
_________________________________________________________________
dropout_2 (Dropout) (None, 128) 0
_________________________________________________________________
dense_2 (Dense) (None, 10) 1290
=================================================================
Total params: 242,062
Trainable params: 242,062
Non-trainable params: 0
_________________________________________________________________
None
2.1 Cross-correlation VS Convolution(★★★★★)
这节内容参考自 一文读懂 12种卷积方法(含1x1卷积、转置卷积和深度可分离卷积等)
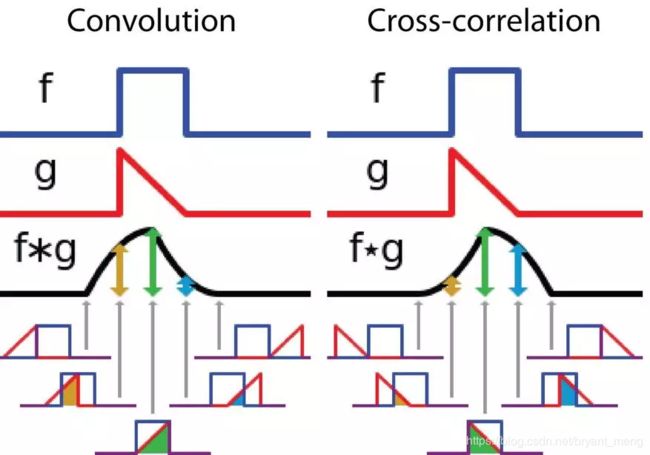
在信号/图像处理领域,卷积的定义是:

其定义是两个函数中一个函数经过反转和位移后再相乘得到的积的积分。下面的可视化展示了这一思想:

信号处理中的卷积。过滤器 g 经过反转,然后再沿水平轴滑动。在每一个位置,我们都计算 f 和反转后的 g 之间相交区域的面积。这个相交区域的面积就是特定位置出的卷积值。
过滤器不经过反转,而是直接滑过函数 f。f 与 g 之间的交叉区域即是互相关。下图展示了卷积与互相关之间的差异。
Cross-correlation: filter 与原图对应位置加权,从上到下,从左到右
Convolution:filter 水平、竖直翻转后(180°),再做相关,直观上看就是从右到左,从下往上
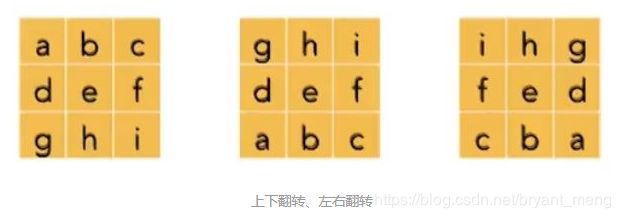
2.2 Max-pooling
Max-pooling, no parameters to learn.:对图片缩减采样,好处如下
- 减少所需处理的数据点:减少后续运算所需要的时间
- 让图像位置差异变小
- 参数的数量和计算量下降:缓解过拟合
The max pooling computation is done independently on each of these n c n_c nc channels. 区别于 Convolution.
2.3 参数量计算
No matter how big the picture is !
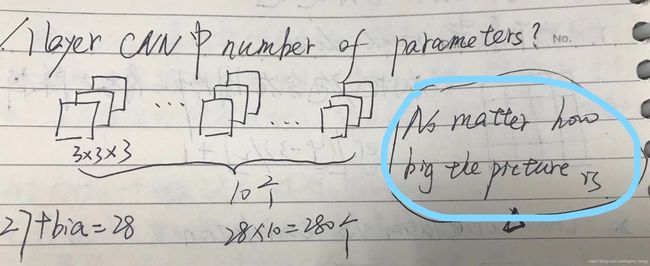
28 * 28 * 1 的图,5 * 5滤波后变成 28 * 28 * 16
1 * 5 * 5 * 16 + 16 = 416(最后的+16是偏置)
14 * 14 * 16 的图,5 * 5滤波后变成 14 * 14 * 36
16 * 5 * 5 * 36+36 = 14436
1764 一维向量全连接到128
1764 * 128 + 128 = 225920
128 一维向量全连接到10
128 * 10 + 10 = 1290
3 Training process
model.compile(loss='categorical_crossentropy',
optimizer='adam',metrics=['accuracy'])
train_history=model.fit(x=x_Train4D_normalize,
y=y_TrainOneHot,validation_split=0.2,
epochs=20, batch_size=300,verbose=2)
同 MLP 的训练,【Keras-MLP】MNIST, epoch改成了20,batch_size改成了300
Output
Train on 48000 samples, validate on 12000 samples
Epoch 1/20
- 10s - loss: 0.4908 - acc: 0.8472 - val_loss: 0.0956 - val_acc: 0.9728
Epoch 2/20
- 2s - loss: 0.1398 - acc: 0.9592 - val_loss: 0.0626 - val_acc: 0.9809
Epoch 3/20
- 2s - loss: 0.1017 - acc: 0.9694 - val_loss: 0.0513 - val_acc: 0.9840
Epoch 4/20
- 2s - loss: 0.0828 - acc: 0.9761 - val_loss: 0.0457 - val_acc: 0.9861
Epoch 5/20
- 2s - loss: 0.0708 - acc: 0.9774 - val_loss: 0.0394 - val_acc: 0.9878
Epoch 6/20
- 2s - loss: 0.0634 - acc: 0.9811 - val_loss: 0.0396 - val_acc: 0.9886
Epoch 7/20
- 2s - loss: 0.0558 - acc: 0.9829 - val_loss: 0.0452 - val_acc: 0.9865
Epoch 8/20
- 2s - loss: 0.0509 - acc: 0.9842 - val_loss: 0.0338 - val_acc: 0.9901
Epoch 9/20
- 2s - loss: 0.0443 - acc: 0.9867 - val_loss: 0.0336 - val_acc: 0.9900
Epoch 10/20
- 2s - loss: 0.0419 - acc: 0.9872 - val_loss: 0.0349 - val_acc: 0.9898
Epoch 11/20
- 2s - loss: 0.0414 - acc: 0.9877 - val_loss: 0.0328 - val_acc: 0.9908
Epoch 12/20
- 2s - loss: 0.0374 - acc: 0.9877 - val_loss: 0.0285 - val_acc: 0.9912
Epoch 13/20
- 2s - loss: 0.0332 - acc: 0.9902 - val_loss: 0.0288 - val_acc: 0.9915
Epoch 14/20
- 2s - loss: 0.0306 - acc: 0.9906 - val_loss: 0.0273 - val_acc: 0.9920
Epoch 15/20
- 2s - loss: 0.0302 - acc: 0.9899 - val_loss: 0.0277 - val_acc: 0.9924
Epoch 16/20
- 2s - loss: 0.0284 - acc: 0.9905 - val_loss: 0.0274 - val_acc: 0.9915
Epoch 17/20
- 2s - loss: 0.0262 - acc: 0.9919 - val_loss: 0.0293 - val_acc: 0.9920
Epoch 18/20
- 2s - loss: 0.0254 - acc: 0.9915 - val_loss: 0.0295 - val_acc: 0.9923
Epoch 19/20
- 2s - loss: 0.0255 - acc: 0.9917 - val_loss: 0.0269 - val_acc: 0.9933
Epoch 20/20
- 2s - loss: 0.0224 - acc: 0.9927 - val_loss: 0.0260 - val_acc: 0.9933
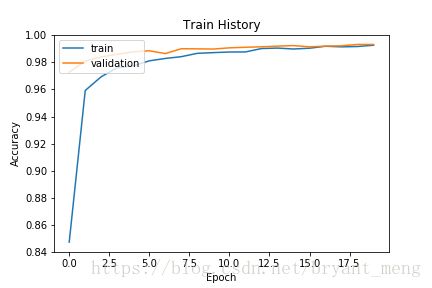
4 可视化训练过程
import matplotlib.pyplot as plt
def show_train_history(train_acc,test_acc):
plt.plot(train_history.history[train_acc])
plt.plot(train_history.history[test_acc])
plt.title('Train History')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.savefig('1.png')
plt.show()
调用准确率
show_train_history('acc','val_acc')
调用损失
show_train_history('loss','val_loss')
可以看到,训练集和验证集的结果很接近,过拟合现象大大减缓,相对于MLP
5 评估模型的precision
scores = model.evaluate(x_Test4D_normalize , y_TestOneHot)
scores[1]
Output
10000/10000 [==============================] - 1s 116us/step
0.9935
6 Predict
预测前10项的结果
prediction=model.predict_classes(x_Test4D_normalize)
prediction[:10]
Output
array([7, 2, 1, 0, 4, 1, 4, 9, 5, 9])
7 可视化预测结果
import matplotlib.pyplot as plt
def plot_images_labels_prediction(images,labels,prediction,idx,num=10):
fig = plt.gcf()
fig.set_size_inches(12, 14)
if num>25: num=25
for i in range(0, num):
ax=plt.subplot(5,5, 1+i)
ax.imshow(images[idx], cmap='binary')
ax.set_title("label=" +str(labels[idx])+
",predict="+str(prediction[idx])
,fontsize=10)
ax.set_xticks([]);ax.set_yticks([])
idx+=1
plt.show()
调用
plot_images_labels_prediction(x_Test,y_Test,prediction,idx=0)
8 Confusion Matrix
import pandas as pd
a = pd.crosstab(y_Test,prediction,rownames=['label'],colnames=['predict'])
print(a)
Output
predict 0 1 2 3 4 5 6 7 8 9
label
0 976 0 0 0 0 0 1 0 2 1
1 0 1132 1 0 0 0 0 1 1 0
2 1 0 1029 0 0 0 0 2 0 0
3 0 0 0 1002 0 5 0 0 2 1
4 0 0 0 0 977 0 1 0 2 2
5 0 0 0 3 0 888 1 0 0 0
6 4 2 0 0 2 1 949 0 0 0
7 0 2 4 0 0 0 0 1017 1 4
8 1 0 1 2 1 1 0 1 964 3
9 0 0 0 0 4 2 0 2 0 1001
不打印的话会画出来漂亮一些的表格,哈哈
显示一下,把5错分为3的情况
df = pd.DataFrame({'label':y_Test, 'predict':prediction})
b = df[(df.label==5)&(df.predict==3)]
print(b)
Output
label predict
1393 5 3
2369 5 3
2597 5 3
第一列是图片id,从0开始编号
声明
声明:代码源于《TensorFlow+Keras深度学习人工智能实践应用》 林大贵版,引用、转载请注明出处,谢谢,如果对书本感兴趣,买一本看看吧!!!