【笔记】计算机的运算方法（一）

一、有符号数

1.原码表示法

  原码是机器数中最简单的一种表示形式，符号位为0表示正数，符号位为1表示负数，数值位即为真值的绝对值，故原码表示又称为带符号的绝对值表示。

  整数原码的定义为

[x]原={0,x2n−x,2n>x≥00≥x>−2n [ x ] 原 = { 0 , x 2 n > x ≥ 0 2 n − x , 0 ≥ x > − 2 n

式中，x为真值，n为整数的位数。

  小数原码的定义为

[x]原={x,1−x,1>x≥00≥x>−1 [ x ] 原 = { x , 1 > x ≥ 0 1 − x , 0 ≥ x > − 1

  当x为0时， [+0.0000]原=0.0000 [ + 0.0000 ] 原 = 0.0000 ， [−0.0000]原=1.0000 [ − 0.0000 ] 原 = 1.0000
  可见原码中的“零”有两种表示形式。

2.补码表示法

补数的概念

  只要确定了“模”，就可找到一个与负数灯架的整数来代替此负数，这样就可把减法运算用加法实现。

• 一个负数可用它的正补数来代替，而这个正补数可以用模加上负数本身求得。
• 一个正数和一个负数互为补数时，它们绝对值之和即为模数。
• 正数的补数即该正数本身。

补码的定义

  整数补码的定义为

[x]补={0,x2n+1+x,2n>x≥00>x≥−2n  (mod 2n+1) [ x ] 补 = { 0 , x 2 n > x ≥ 0 2 n + 1 + x , 0 > x ≥ − 2 n     ( m o d   2 n + 1 )

  小数补码的定义为

[x]补={x,2+x,1>x≥00>x≥−1  (mod 2n+1) [ x ] 补 = { x , 1 > x ≥ 0 2 + x , 0 > x ≥ − 1     ( m o d   2 n + 1 )

  当x为0时， [+0]补=[−0]补=0.0000 [ + 0 ] 补 = [ − 0 ] 补 = 0.0000 ，即补码中的“零”只有一种表示形式。由于补码中的零只有一种表示形式，故它比原码能多表示一个“-1”。

  当模数为4时，形成双符号位的补码。这种双符号位的补码又称为变形补码，它在阶码运算和溢出判断中有其特殊作用。如x=-0.1001，对 mod 22 m o d   2 2 而言， [x]补=22+x=100.0000−0.1001=11.0111 [ x ] 补 = 2 2 + x = 100.0000 − 0.1001 = 11.0111

  对于负数，由 [x]补 [ x ] 补 求 [x]原 [ x ] 原 和由 [x]原 [ x ] 原 求 [x]补 [ x ] 补 都可用规则除符号位外，每位求反，末尾加一。

  不论真值是正还是负，由 [x]补 [ x ] 补 求 [−x]补 [ − x ] 补 求都是采用规则连同符号位在内，每位取反，末尾加一。

反码表示法

  反码同行用来作为由原码求补码或者由补码求原码的中间过渡。
  整数反码的定义为

[x]反={0,x(2n+1−1)+x,2n>x≥00≥x>−2n  (mod（2n+1−1）) [ x ] 反 = { 0 , x 2 n > x ≥ 0 ( 2 n + 1 − 1 ) + x , 0 ≥ x > − 2 n     ( m o d （ 2 n + 1 − 1 ） )

  小数反码的定义为

[x]反={x,(2−2−n)+x,1>x≥00≥x>−1  (mod(2−2−n)) [ x ] 反 = { x , 1 > x ≥ 0 ( 2 − 2 − n ) + x , 0 ≥ x > − 1     ( m o d ( 2 − 2 − n ) )

  当x为0时， [+0.0000]反=0.0000 [ + 0.0000 ] 反 = 0.0000
        [−0.0000]反=(10.0000−0.0001)−0.0000=1.1111 [ − 0.0000 ] 反 = ( 10.0000 − 0.0001 ) − 0.0000 = 1.1111
  可见 [+0]反 [ + 0 ] 反 不等于 [−0]反 [ − 0 ] 反 ，反码中的“零”有两种表示形式。

  实际上，反码也可看作是 mod(2−2−n) m o d ( 2 − 2 − n ) （对于小数）或 mod（2n+1−1） m o d （ 2 n + 1 − 1 ） （对于整数）的补码。与补码相比，仅在末尾差1，故也称小数的补码为2的补码，小数的反码为1的补码。

  对于负数，由 [x]反 [ x ] 反 求 [x]原 [ x ] 原 和由 [x]原 [ x ] 原 求 [x]反 [ x ] 反 都可用规则除符号位外，每位求反。

---

  三种机器数的特点可归纳如下：

• 三种机器数的最高位均为符号位。符号位和数值部分之间可用“.”（对于小数）或“,”（对于整数）隔开。
• 当真值为正时，原码、补码和反码的表示形式均相同，即符号位用“0”表示，数值部分与真值相同。
• 当真值为负时，原码、补码和反码的表示形式不同，但其符号位都用“1”表示，而数值部分有这样的关系：补码是原码的“求反加一”，反码是原码的“每位求反”。

移码表示法

  移码的定义为

[x]移=2n+x (2n>x≥−2n) [ x ] 移 = 2 n + x   ( 2 n > x ≥ − 2 n )

  其实移码就是在真值上加一个常数 2n 2 n 。在数轴上移码所表示的范围恰好对应于真值在数轴上的范围向轴的正方向移动 2n 2 n 个单元，故称为移码。

  当x为0时， [+0]移=[−0]移=1.0000 [ + 0 ] 移 = [ − 0 ] 移 = 1.0000 ，即移码中的“零”只有一种表示形式，故它比原码能多表示一个负数。
  移码的最小真值为全0。利用移码的这一特点，当浮点数的阶码用移码表示时，就能很方便地判断阶码的大小。
  同一个真值的移码和补码仅差一个符号位，若将补码的符号位由“0”改为“1”或从“1”改为“0”，即可得该真值的移码。

二、数的定点表示和浮点表示

  共有两种方法表示小数点的存在，即定点表示和浮点表示。定点表示的数称为定点数，浮点表示的数称为浮点数。

1.定点表示

  小数点在某一位置的数为定点数，有以下两种格式。

  当小数点位于数符和第一数值位之间时，机器内的数为纯小数；当小数点位于数值位之后时，机器内的数为纯整数。采用定点数的机器称为定点机。数值部分的位数n决定了定点机中数的表示范围。若机器数采用原码，小数定点机中的数的表示范围是 −(1−2−n) − ( 1 − 2 − n ) ~ (1−2−n) ( 1 − 2 − n ) ，整数定点机中数的表示范围是 −(2n−1) − ( 2 n − 1 ) ~ (2n−1) ( 2 n − 1 ) 。
  在定点机中，由于小数点的位置固定不定，故当机器处理的数不是纯小数或纯整数时，必须乘上一个比例因子，否则会产生“溢出”。

2.浮点表示

  浮点数即小数点的位置可以浮动的数。
  通常浮点数被表示成

N=S×rj N = S × r j

式中，S为尾数，j为阶码，r是基数。在计算机中，基数可取2、4、8、16等。
  为了提高数据精度以及便于浮点数的比较，在计算机中规定浮点数的尾数用纯小数形式。将尾数最高位为1的浮点数称为 规格化数。浮点数表示成规格化形式后，其精度最高。

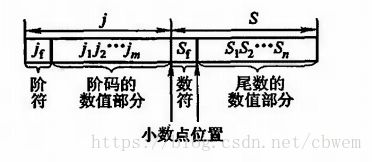
浮点数的表示形式

  采用这种数据格式的机器称为浮点机。

  浮点数由阶码j和尾数S两部分组成。阶码是整数，阶符和阶码的位数m合起来反映浮点数的表示范围及小数点的实际位置；尾数是小数，其位数n反映了浮点数的精度；尾数的符号 Sf S f 代表浮点数的正负。

浮点数的表示范围

  设浮点数阶码的数值位取m位，尾数的数值位取n位，当浮点数为非规格化数时，它在数轴上的表示范围如下。

  最大正数为 22m−1×(1−2−n) 2 2 m − 1 × ( 1 − 2 − n ) ；最小正数为 2−(2m−1)×2−n 2 − ( 2 m − 1 ) × 2 − n ；最大负数为 −2−(2m−1)×2−n − 2 − ( 2 m − 1 ) × 2 − n ；最小负数为 −22m−1×(1−2−n) − 2 2 m − 1 × ( 1 − 2 − n ) 。
  当浮点数阶码大于最大阶码时，称为上溢，此时机器停止运算，进行中断溢出处理；当浮点数阶码小于最小阶码时，称为下溢，此时溢出的数绝对值很小，通常将尾数各位强置为0，按机器零处理，此时机器可以继续运行。

  一旦浮点数的位数确定后，合理分配阶码和尾数的位数，直接影响浮点数的表示范围和精度。对于短实数（总位数为32位），阶码取8位（含阶符1位），尾数取24位（含数符1位）；对于长实数（总位数为64位），阶码取11位（含阶符1位），尾数取53位（含数符1位）；对于临时实数（总位数为80位），阶码取15位（含阶符1位），尾数取65位（含数符1位）。

  当一个浮点数尾数为0时，不论其阶码为何值；或阶码等于或小于它所能表示的最小数时，不管其尾数为何值，机器都把该浮点数作为零看待，并称之为机器零。如果浮点数的阶码用移码表示，尾数用补码表示，则当阶码为它所能表示的最小数 2−m 2 − m 且尾数为0时，其阶码（移码）全为0，尾数（补码）也全为0，这样的机器零为000…00000，全零表示有利于简化机器中判“0”电路。

浮点数的规格化

  将非规格化数转换成规格化数的过程称为规格化。对于技术不同的浮点数，因其规格化数的形式不同，规格化过程也不同。
  当基数为2时，尾数最高位为1的数为规格化数。规格化时，尾数左移一位，阶码减1（称为左规）；尾数右移一位，阶码加1（称为右规）。
  当基数为4时，尾数最高两位不全为零的数为规格化数。规格化时，尾数左移两位，阶码减1；尾数右移两位，阶码加1。
  当基数为8时，尾数最高三位不全为零的数为规格化数。规格化时，尾数左移三位，阶码减1；尾数右移三位，阶码加1。

  一般来说，基数r越大，可表示的浮点数范围越大，而且所表示的数的个数也越多。但r越多，浮点数的精度反而下降。

3.定点数和浮点数的比较

• 当浮点机和定点机中数的位数相同时，浮点数的表示范围比定点数大得多。
• 当浮点数为规格化数时，其相对精度远比定点数高。
• 浮点数运算要分阶码部分和尾数部分，而且运算结果都要求规格化，故浮点运算步骤比定点运算步骤多，运算速度比定点运算的低，运算线路比定点运算的复杂。
• 在溢出的判断方法上，浮点数是对规格化数的阶码进行判断，而定点数是对数值本身进行判断。

  浮点数在数的表示范围、数的精度、溢出处理和程序编程方面（不取比例因子）均优于定点数。到哪在运算规则、运算速度及硬件成本方面又不如定点数。

4.IEEE 754标准

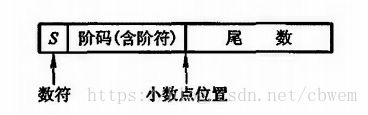
  浮点数一般采用IEEE指定的国际标准，这种标注形式如下。

  按IEEE标准，常用的浮点数有三种：

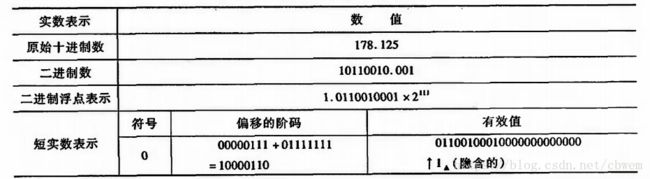
  阶码用移码表示，阶码的真值都被加上一个常数（偏移量），如短实数、长实数、临时实数的偏移量用十六进制数表示分别为7FH、3FFH、3FFFH。尾数部分通常都是规格化表示，即非“0”的有效位最高位总是“1”，但在IEEE标准中，有效位呈如下形式。

1♠ffff……fff 1 ♠ f f f f … … f f f

其中 ♠ ♠ 表示假想的二进制小数点。在实际表示中，对短实数和长实数，这个整数位的1省略，称 隐藏位；对于临时实数不采用隐藏位方案。