Towards Real-Time Multi-Object Tracking
文章：https://arxiv.org/pdf/1909.12605v1.pdf
代码：https://github.com/Zhongdao/Towards-Realtime-MOT
0 摘要
现代的多目标追踪(MOT)系统大多遵循基于检测的追踪这一实现思路。该类思路的实现一般包括两个模型，一个是目标检测模型用于目标定位，另一个是目标表观特征提取模型用于目标关联。一般算法都是使用两个不同的模型分别完成检测和特征提取任务，这样在执行目标追踪任务时，总的耗时是两个模型耗时的总和，这样很容易降低追踪系统的执行效率。现有的MOT算法大多关注于实时目标匹配而不是实时MOT系统。本文，作者提出了使用单个共享模型同时完成目标检测和目标表观特征提取任务，即将目标特征任务合并到一个单阶段的目标检测模型中，这样该模型可以同时输出目标检测框和表观特征。这样就形成了一个多任务学习问题，即同时完成目标分类、bounding box回归和表观特征学习，损失函数是三个子任务的加权和。最终得到了SOTA的追踪效果，并且根据不同分辨率的输入图像，可以以18.8到24.1FPS进行MOT。
1 简介
基于检测的追踪包括两个步骤：
- 目标检测：在图像上定位目标；
- 目标关联：将当前帧检测到的目标和已存在的目标轨迹相关联。目标关联中一般都会用到目标重识别(re-ID)模型。
一般都是使用两个独立的模型分别完成上述两个任务，作者称之为SDE(Separate Detection and Embedding)。因为用到了两个模型，所以往往效率不太理想。
因为上述两个模型可以共享低层特征，因此完全可以使用一个模型完成两个任务。直观的想法是可以使用Faster R-CNN同时完成这两个任务，Faster R-CNN中的RPN保持不变，用于bounding box定位，但R-CNN模型可以修改成有监督的特征学习而不是进行有监督的目标分类。尽管这样修改可以提升效率，但由于受限于两阶段设计，一般运行效率低于10FPS，达不到实时运行的需求。这种方法这里称作Two-Stage方法。
作者提出了JDE(Jointly learns the Detetor and Embedding model)，同时完成目标检测和表观特征学习。
SDE、Two-Stage Method和JDE的区别如图1所示。
为实现JDE，需要实现多个关键组件：训练数据、网络结构、目标函数、优化策略和验证准则。首先结合6个行人检测和行人搜索公开数据集形成一个大的标注数据集，这个数据集中标注了所有行人的位置信息和部分行人的身份信息；其次，选定FPN作为骨干网络；第三，这样一个多任务学习问题包括了anchor分类、bbox回归和表观特征学习三个子任务，作者采用Multi-task learning using uncertainty to
weigh losses for scene geometry and semantics.介绍的利用任务的不确定性动态进行损失的加权。最后，使用AP(Average Percision)衡量检测的效果，使用检索的TAR和FPR衡量表观特征的优劣，使用CLEAR标准衡量MOT的准确率，尤其关注MOTA。
2 检测和表观特征联合学习
JDE的目标是在单次前向运算过程中输出检测框和目标的外观特征。
将数据集表示为 { I , B , y } i = 1 N \{I,B,y\}_{i=1}^N {I,B,y}i=1N， I ∈ R c × h × w I \in R^{c \times h \times w} I∈Rc×h×w表示一个视频帧， B ∈ R k × 4 B \in R^{k \times 4} B∈Rk×4表示该视频帧中标注的k个目标的位置信息， y ∈ z k y \in z^{k} y∈zk表示标注的目标身份信息，-1则表示该目标未标注身份信息。JDE的目标是预测bounding box B ^ ∈ R k ^ × 4 \hat B \in R^{{\hat k} \times 4} B^∈Rk^×4和表观特征 F ^ ∈ R k ^ × D \hat F \in R^{\hat k \times D} F^∈Rk^×D，D表示各目标的特征维度。JDE应该满足下述要求：
- B ^ \hat B B^应该和B尽可能接近；
- 给定距离度量 d ( . ) d(.) d(.)，对任意的三元组 ( k t , k t + Δ t , k t + Δ t ′ ) (k_t,k_{t+\Delta t,k^{'}_{t+\Delta t}}) (kt,kt+Δt,kt+Δt′)满足 y k t + Δ t = y k t y_{k_{t+\Delta t}} = y_{k_t} ykt+Δt=ykt且 y k t + Δ t ′ ≠ y k t y_{k^{'}_{t+\Delta t}} \neq y_{k_t} ykt+Δt′=ykt，有 d ( f k t , f k t + Δ t ) < d ( f k t , f k t + Δ t ′ ) d(f_{k_t},f_{k_{t+\Delta t}}) < d(f_{k_t},f_{k^{'}_{t+\Delta t}}) d(fkt,fkt+Δt)<d(fkt,fkt+Δt′)。 f k t f_{k_t} fkt是 F ^ t \hat{F}_t F^t的一个行向量， f k t + Δ t f_{k_{t+\Delta t}} fkt+Δt和 f k t + Δ ′ f_{k^{'}_{t+\Delta}} fkt+Δ′是来自于 F ^ t + Δ t \hat F_{t + \Delta t} F^t+Δt的行向量。
上述两个目标函数，第一个是要求检测尽可能准确；第二个是要求同一个目标不同帧之间的表观特征要比不同目标不同帧之间的表观特征距离小。距离度量函数可以是欧氏距离或余弦距离。理论上来说，如果上述两个目标函数可以很好的满足，那么即便使用最简单的关联策略，例如匈牙利算法，也可以产生良好的追踪效果。
整体网络：
使用FPN作为骨干网络，FPN使用多尺度的特征进行目标检测，可以检测不同尺度大小的行人目标。图2简单介绍了JDE的网络结构，输入视频帧通过骨干网络的前向计算过程获取了三个尺度的特征图，分别将空间尺寸下降了32，16和8倍。然后将空间尺寸最小的特征图(对应最强的语义特征)进行上采样，然后和第二小的特征图使用skip connection进行融合。对其他的尺度也进行相同的操作。最后，将基于三个尺度融合的特征图的预测头进行相加。预测头由数个堆砌的卷积层组成，输出尺寸为(6A+D) * H * W的预测。A表示各尺度的anchor box的数目，D是特征embedding的维度。最终的密集预测分为三部分：
- box分类结果，大小为 2A * H * W；
- box回归系数，大小为 4A * H * W；
- 特征embedding的尺寸，大小为 D * H * W。
学习检测：
检测分支和RPN很接近，但有两项修改。第一个，针对行人目标，重新设计了anchor的数量、大小和长宽比。基于先验知识，所有的anchor框的宽高比设置为1：3；设置A=4，即各尺度包含4个anchor，3个尺度共12个；anchor的宽度从 11 ≈ 8 × 2 1 2 11 \approx 8 \times 2^{\frac{1}{2}} 11≈8×221到 512 ≈ 8 × 2 12 2 512 \approx 8 \times 2^{\frac{12}{2}} 512≈8×2212。第二个，是关于判定各anchor属于前景和背景的阈值，按照惯例，如果某anchor和ground truch的IOU大于0.5则认为其是前景目标，如果某anchor和任意ground truth的IOU都小于0.4，则认为该anchor表示背景。这里作者使用了0.4，而不是普遍使用的0.3，这样会使得更多的少量重叠的目标被判定为背景，有助于减少误报率，在高度重叠的场景下比较有益。
检测的目标函数包含两部分，分别是分类损失和定位损失，分类损失使用交叉熵损失，定位损失使用smooth-L1损失，和Faster R-CNN一致。
学习表观特征：
第二个问题是学习表观特征，目的是使得同一目标表观特征的差异比不同目标的表观特征的差异小。可以使用三元组达到这个目的。使用三元组损失 L t r i p l e t = max ( 0 , f T f − − f T f + ) L_{triplet} = \max(0,f^Tf^- - f^Tf^+) Ltriplet=max(0,fTf−−fTf+)，其中 f T f^T fT表示mini-batch中被选为anchor的实例， f + f^+ f+表示和 f T f^T fT对应的正例， f − f^- f−表示和 f T f^T fT对应的负例。原始形式的三元组损失难以优化，首要原因就是训练集具有巨大的采样空间。本文中，我们在单个mini-batch中最小化所有负例和最难优化的正例的损失来接近问题，即
L t r i p l e t = ∑ i max ( 0 , f T f i − − f T f + ) (1) L_{triplet} =\sum_i \max(0,f^Tf^-_i - f^Tf^+) \tag{1} Ltriplet=i∑max(0,fTfi−−fTf+)(1)
f + f^+ f+表示一个mini-batch中最难优化的正例。
三元组损失的第二个挑战是损失函数值不稳定且收敛速度慢。为了稳定训练过程并加速收敛过程，这里优化三元组损失的smooth上限。即
L u p p e r = log ( 1 + ∑ i exp ( f T f i − − f T f + ) ) (2) L_{upper} =\log (1 + \sum_i \exp(f^Tf^-_i - f^Tf^+)) \tag{2} Lupper=log(1+i∑exp(fTfi−−fTf+))(2)
式（2）可以变换成：
L u p p e r = − log ( exp ( f T f + ) exp ( f T f + ) + ∑ i exp ( f T f i − ) ) (3) L_{upper} =-\log (\frac{\exp(f^Tf^+)}{\exp(f^Tf^+)+\sum_i\exp(f^Tf^-_i)}) \tag{3} Lupper=−log(exp(fTf+)+∑iexp(fTfi−)exp(fTf+))(3)
式(3)和交叉熵损失的表达式很接近，
L C E = − log ( exp ( f T g + ) exp ( f T g + ) + ∑ i exp ( f T g i − ) ) (4) L_{CE} =-\log (\frac{\exp(f^Tg^+)}{\exp(f^Tg^+)+\sum_i\exp(f^Tg^-_i)}) \tag{4} LCE=−log(exp(fTg+)+∑iexp(fTgi−)exp(fTg+))(4)
这里将anchor属于正类的概率表示为 g + g^+ g+，属于负类的概率表示为 g − g^- g−。 L u p p e r L_{upper} Lupper和 L C E L_{CE} LCE主要有两个方面的区别，一是，交叉熵损失使用样本属于某类别的概率而不是直接使用样本的特征向量；第二，参与 L C E L_{CE} LCE计算的所有负类是样本空间中的所有负类，但在 L U p p e r L_{Upper} LUpper中，仅是使用mini-batch中的负例。
基于上面的分析，可以得知 L C E > L U p p e r > L t r i p l e t L_{CE} > L_{Upper} > L_{triplet} LCE>LUpper>Ltriplet(由于 L u p p e r L_{upper} Lupper中负类数量少，所以其分母小于 L C E L_{CE} LCE的分母，-log是单调减函数，所以 L C E > L U p p e r L_{CE} > L_{Upper} LCE>LUpper），下面的实验结果也证明了这一点。所以，我们选择交叉熵损失作为特征学习的损失函数，表示为 L γ L_{\gamma} Lγ。
如果一个anchor框被标记为前景，对应的特征向量提取自密集特征图。提取的特征被送入一个共享的全连接层输出各类的logits，基于该logits可以计算交叉熵损失。以这种方式，来自于多个尺度的特征共享相同的空间，使得跨尺度关联变得可行。具有box标记但不具有身份标记的前景目标在计算embedding损失时会被忽略。
自动损失平衡：
JDE每一个预测头可以认为是多任务学习模型。总的损失可以认为是各层各组件损失的线性加权。
L t o t a l = ∑ i = 1 M ∑ j = α , β , γ w j i L j i (5) L_{total} = \sum_{i=1}^M\sum_{j=\alpha,\beta,\gamma}w_j^iL_j^i \tag{5} Ltotal=i=1∑Mj=α,β,γ∑wjiLji(5)
M是预测头的数量， w j i , i = 1 , ⋯ , M , j = α , β , γ w_j^i,i=1,\cdots,M,j=\alpha,\beta,\gamma wji,i=1,⋯,M,j=α,β,γ为加权系数。
可以按照下述方式计算损失权重系数：
- 设置 w α i = w β j w_{\alpha}^i=w_{\beta}^j wαi=wβj，即令检测中的分类损失和定位损失同等重要；
- 设置 w α 1 = ⋯ = w α M , w β 1 = ⋯ = w β M , w γ 1 = ⋯ = w γ M w_{\alpha}^1=\cdots=w_{\alpha}^M,w_{\beta}^1=\cdots=w_{\beta}^M,w_{\gamma}^1=\cdots=w_{\gamma}^M wα1=⋯=wαM,wβ1=⋯=wβM,wγ1=⋯=wγM，即各尺度的损失同等重要；
- 根据上面的设置，需要确定两个参数 w α w_{\alpha} wα和 w γ w_{\gamma} wγ，使用穷举法去找最优参数。
上述限制太强了，有可能找不到最优权重系数。另外穷举法也比较耗时。作者采用Multi-task learning using uncertainty to weigh losses for scene geometry and semantics提出的基于任务的不确定性独立去计算加权系数。最终自动加权的损失写为：
L t o t a l = ∑ i = 1 M ∑ j = α , β , γ 1 2 ( 1 e s j i L j i + s j i ) (6) L_{total} = \sum_{i=1}^M\sum_{j=\alpha,\beta,\gamma}\frac{1}{2}(\frac{1}{e^{s^i_j}}L_j^i+s_j^i) \tag{6} Ltotal=i=1∑Mj=α,β,γ∑21(esji1Lji+sji)(6)
s j i s_j^i sji为每个任务的不确定性，用可学习的参数进行表示。
实时关联：
虽然关联算法不是作者关心的重点，但还是介绍了一种简单高效的实时关联算法。
对于给定的视频，JDE模型给出了每一个目标的bounding box和表观特征，从而可以计算出新检测目标的表观特征和已存在的目标轨迹的表观特征之间的关联矩阵。可以使用匈牙利算法进行检测目标和历史追踪轨迹的关联。使用kalman滤波器进行轨迹平滑和目标位置预测。如果某个被被关联的检测框和预测框空间位置相距很远，则删除这个关联。使用下述公式为已关联的检测和轨迹进行表观特征更新：
f t = η f t − 1 + ( 1 − η ) f ^ (7) f_t = \eta f_{t-1} + (1 - \eta)\hat f \tag{7} ft=ηft−1+(1−η)f^(7)
f ^ \hat f f^表示被关联的检测目标的表观特征， f t f_t ft表示在时刻t追踪目标的表观特征。 η \eta η = 0.9，是指数加权移动平均的系数。如果某个追踪目标没有被关联到，则认为目标有可能是消失了，在超过一定的时间限制后将目标删除；如果后面潜在的消失目标被重新关联了，则认为是目标可能暂时被遮挡造成的，进行继续跟踪处理。（实时关联部分和Deepsort的思想很接近，除了这里使用了表观特征的指数加权移动平均，使用指数加权移动平均从理论上分析更容易把发生交叉时误匹配的追踪再修正回来，后面可以在工程上测试下效果）。
实验：
数据集和验证标准：在小的数据集上进行实验可能造成结果偏差，也有可能造成算法不适用于大规模数据集。所以，作者整合了6个公开的行人检测、MOT和行人检索数据集构建了一个大的训练集。这些数据集可以分为两类，一类是只包含目标位置标注信息的数据集，另一类是既包含目标位置信息也包含了目标身份信息的数据集。ETH数据集和MOT16的测试集存在重合数据，对其进行了删除处理。整个的数据集如表1所示。
进行性能评估，需要考虑检测精度、表观特征的区分能力和整个MOT系统的追踪性能三个方面。使用和Caltech验证集上的[email protected]表征检测性能。对Caltech验证集、CUHK-SYSU数据集和PRW数据集中所有前景目标进行特征提取，然后进行1：N目标检索，使用@FAR=0.1时的TPR衡量表观特征。使用CLEAR标准评估整个MOT系统。使用MOT-15剔除了重复数据的训练集做验证集，使用MOT16的测试集比较各模型的性能。
实现细节：使用Draknet53作为骨干网络，使用标准SGD训练30个epoch。学习率初始化为0.01，在第15和23个epoch时变为原来的0.1倍。使用了数据增强，输入图像的分辨率为1088*608。
实验结果：
比较使用三个不同的损失函数进行外观特征训练的结果：比较使用交叉熵损失、三元组损失及三元组上限损失训练外观特征的区别。对于三元组损失 L t r i p l e t L_{triplet} Ltriplet和三元组上限损失 L u p p e r L_{upper} Lupper，从连续的视频帧中选取 B / 2 B/2 B/2个目标对形成大小为B的mini-batch。这样可以保证始终存在正样本对。对于交叉熵损失，不需要特殊的样本采样策略，通过随机采样组成mini-batch。表二给出了使用不同损失函数的对比结果。
前三行的结果表明，交叉熵损失的效果最好。令人惊讶的是，Emb的性能提升了40多。可能的原因是交叉熵损失希望一个样本属于真实类的概率比该样本属于错误类的概率都大。交叉熵损失比仅在一个mini-batch中要求的三元组损失更加严格。基于这个实验结果，JDE中使用交叉熵损失。
比较不同的损失加权策略：作者共比较了五种损失加权策略，第一种是所有损失的权重都一致，表示为“Uniform”；第二种是使用“自动损失平衡”一节介绍的第一种搜索方法得到的权重损失，称之为“App.Opt”；第三种是使用各自损失幅值移动平均的倒数，称之为“Loss.Norm”；第四种是“Multi-task learning as multi-objective optimization”提出的“MGDA-UB”；第五种是根据不确定性自动加权策略。五种不同损失函数取得的效果如表二的下面五行所示。
首先，使用Uniform策略时检测效果很差，因此也会对追踪效果造成负面影响。这是因为embedding损失的幅值远大于分类和bounding box定位的损失，因此训练过程中针对检测训练的力度不够。如果我们让所有的损失按照相似的比例被对待，如“APP.Opt”所示，就可以取得较好的检测和embedding结果。表2可以看出使用不确定性自动确定权重的方法效果最好。
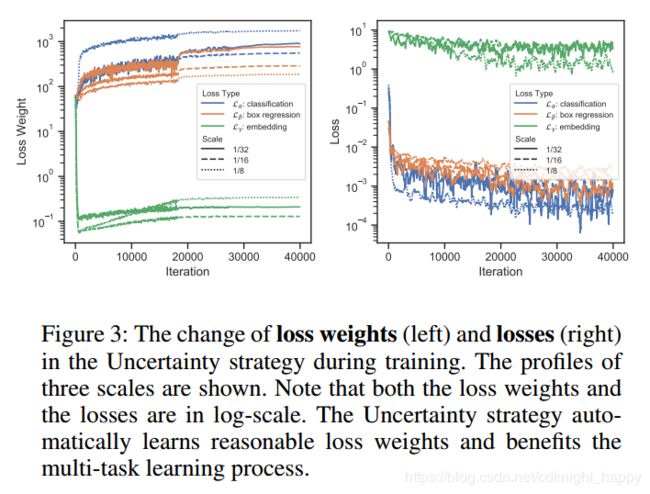
图3给出了使用不确定加权损失训练过程中各损失系数的变化情况。左图是分类、定位和embedding的损失加权系数，右图是对应的各项损失。可以观测到虽然各损失系数进行了正则初始化，但embedding损失的系数很快下降到了0.1左右，而其他两项损失的系数很快增加到了100左右。这和采用“App.Opt”方法学得的最优系数(64:0.1)很接近，但因为损失系数可以实时学习，因此使用不确定性方法学得的系数具有最好的追踪精度。
和SDE方法进行比较：
和其他SOTA MOT系统对比：
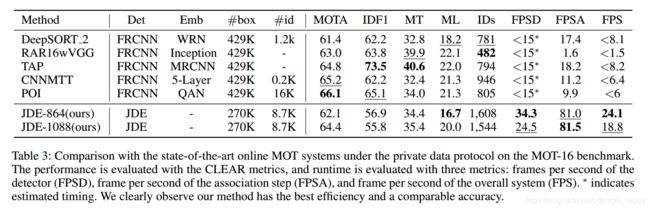分析和讨论：
JDE的一个缺点是IDF1值较低，ID Switch较多。一开始作者认为是JDE学习的表观特征的较差造成的，但是作者使用单独学习的表观特征提取模型更换之后，发现IDF1值和ID Switch变化不大。最终作者发现这主要是因为行人交叉时目标检测的精度不足造成的。图5给出了一个失败示例，未来作者的工作也主要关注目标交叉时检测精度的提升。
个人看法：一直以来，在工程上特别希望能通过一个模型完成检测和表观特征提取，这样才能提高处理效率。终于看到有人实现了这个思路，给作者点赞。作者也公布了代码，下面要好好研究下代码，另外，这里将draknet53结合FPN、基于不确定性进行损失加权、使用交叉熵代替三元损失都值得好好学习，作者厉害。