动态规划实战：如何实现搜索引擎中的拼写纠错功能？

------ 本文是学习算法的笔记，《数据结构与算法之美》，极客时间的课程 ------

在Trie 树那节，我们讲过，利用 Trie 树，可以实现搜索引擎的关键词提示功能，这样可以节省用户输入搜索关键词的时间。实际上，搜索引擎在用户体验方面的优化还有很多，比如你可能经常会用的拼写纠错功能。

当你在搜索框中，一不小心输错单词，搜索引擎会非常智能地检测出你的拼写错误，并且用对应的正确的单词来进行搜索。作为一名软件开发工程师，这个功能你该怎么实现呢？

如何量化两个字符串的相似度？

计算机只认识数字，所以要解答开篇的问题，我们就要先来看，如何量化两个字符串之间的相似程度呢？有一个非常著名的量化方法，那就是编辑距离（Edit Distance）

顾名思义，编辑距离指的就是，将一个字符串转化成另一个字符串，需要的最少编辑操作次数（比如增加一个字符、删除一个字符、替换一个字符）。编辑距离越大，说明两个字符串的相似程度越小；相反，编辑距离越小，说明两个字符串的相似程度越大。对于两个完全相同的字符串来说，编辑距离就是0。

根据所包含的编辑操作种类不同，编辑距离有多种不同的计算方式，比较著名的有莱文斯坦距离（Levenshtein distance）和最长公共子串长度（Longest common substring length）。其中，莱文斯坦距离允许增加、删除、替换三个编辑操作，最长公共子串长度只允许增加、删除字符两个编辑操作。

而且，莱文斯坦距离和最长公共子串长度，从两个截然相反的角度，分析字符串的相似程度。莱文斯坦距离的大小，表示两个字符串差异的大小；而公共最长子串的大小，表示两个字符串相似的程度大小。

关于这两个计算方法，我举个例子说明一下。这里面，两个字符串 mitcmu 和 mtacnu 的莱文斯坦距离是3，最长公共子串长度是4。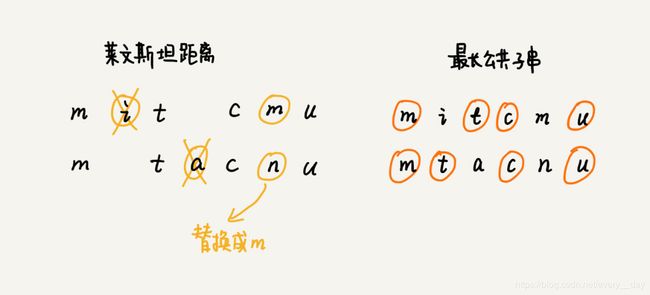
了解了编辑距离的概念之后，我们来看，如何快速计算两个字符串之间的编辑距离。

如何编程计算莱文斯坦距离？

之前我反复强调过，思考过程比结论更重要，所以，我现在展示下，解决这个问题， 我的完整的思考过程。

这个问题是把一个字符串变成另一个字符串，需要最少编辑次数。整个求解过程，涉及多个决策阶段，我们老板娘依次考察一个字符串中的每个字符，跟另一个字符串中的字符是否匹配，匹配的话如何处理，不匹配的话又如何处理。所以，这个问题符合多阶段决策最优解模型。

我们前面讲了，贪心、回溯、动态规划可以解决的问题，都可以抽象成这样一个模型。要解决这个问题，我们可以先看一看，用最简单的回溯算法，该如何来解决。

回溯是一个递归处理的过程。如果 a[i] 和 b[j] 匹配，我们递归考察 a[i+1] 和 b[j+1]。如果a[i] 和 b[j]不匹配，那我们有多种处理方式可选：

• 可以删除 a[j]，然后递归考察 a[i+1] 和 b[j]；
• 可以删除 b[j]，然后递归考察 a[i] 和 b[j+1]；
• 可以在 a[i] 前面添加一个和 b[j] 相同的字符，然后递归考察a[i] 和 b[j+1]；
• 可以在 b[i] 前面添加一个和 a[j] 相同的字符，然后递归考察a[i+1] 和 b[j]；
• 可以将 a[i] 替换成 b[j]，或者将 b[j] 替换成 a[i]，然后递归考察a[i+1] 和 b[j+1]；

我们将上面的回溯算法的处理思路，翻译成代码，就是下面这个样子。

    private char[] a = "mitcmu".toCharArray();
    
    private char[] b = "mtacun".toCharArray();
    
    private int n = 6;
    private int m = 6;
    
    private int minDist = Integer.MAX_VALUE; // 存储结果
    public void lwstBT(int i, int j, int edist) {
    	if (i == n || j == m) {
			if (i < n) {
				edist += (n - i);
			}
			if (j < m) {
				edist += (m - j);
			}
			if (edist < minDist) {
				minDist = edist;
			}
			return;
		}
    	if (a[i] == b[j]) { // 两个字符匹配
    		lwstBT(i + 1, j + 1, edist);
		}else {
			lwstBT(i + 1, j, edist + 1); // 删除a[i]或者b[j]前添加一个字符
			lwstBT(i, j + 1, edist + 1); // 删除b[j]或者a[i]前添加一个字符
			lwstBT(i + 1, j + 1, edist + 1); // 将a[i]或者b[j]替换为相同的字符
		}
    }

根据回溯算法的代码实现，我们可以画出递归树，看是否存在重复子问题。如果存在重复子问题，那我们就可以考虑能否用动态规划来解决； 如果不存在重复子问题，那回溯就是最好的解决方法。

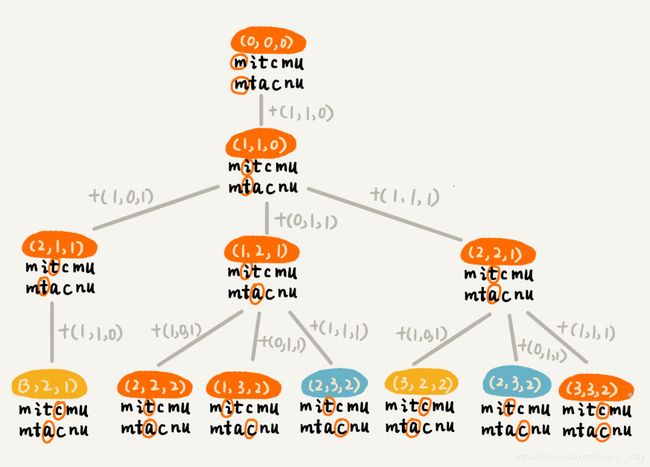
在递归树中，每个节点代表一个状态，状态包含三个变量（i, j, edist），其中，edist 表示处理到 a[i] 和 b[j] 时，已经执行的编辑操作的次数。

在递归树中，（i, j）两个变量的节点很多，比如（3，2）和（2，3）。对于（i, j）相同的节点，我们只需要保留 edist 最小的，继续递归处理就可以了，剩下的节点都可以舍弃。所以，状态就从（i, j, edist）变成了（i, j, min_edist），其中 min_edist 表示处理到 a[i] 和 b[j]，已经执行的最少编辑次数。

看到这里，你有没有觉得，这个问题跟上两节的动态规范例子非常相似？不过，这个问题的状态转移方式，要比之前两节课中讲到的例子都要复杂很多。上一节我们讲的矩阵最短路径问题中，到状态（i, j）只能通过（i-1, j）或（i, j-1）两个状态转移过来，而今天这个问题，状态（i, j）可能从（i-1, j），（i, j-1），（i-1, j-1）三个状态中的任意一个转移过来。

基于刚刚的分析，我们可以尝试着将状态转移的过程，用公式写出来。这就是我们前面讲的状态转移方程。

• 如果：a[i] != b[j]，那么：min_edist(i, j) 就等于：min( min_edist( i-1,j)+1, min_edist( i, j-1)+1, min_edist( i-1,j-1)+1)
• 如果： a[i] == b[j]，那么：min_edist(i, j) 就等于：min( min_edist( i-1,j)+1, min_edist( i, j-1)+1, min_edist( i-1,j-1))
• 其中，min表示三数中的最小值。

了解了状态与状态之间的递推关系，我们画出一个二维的状态表，按行依次来填充状态表中的每个值。

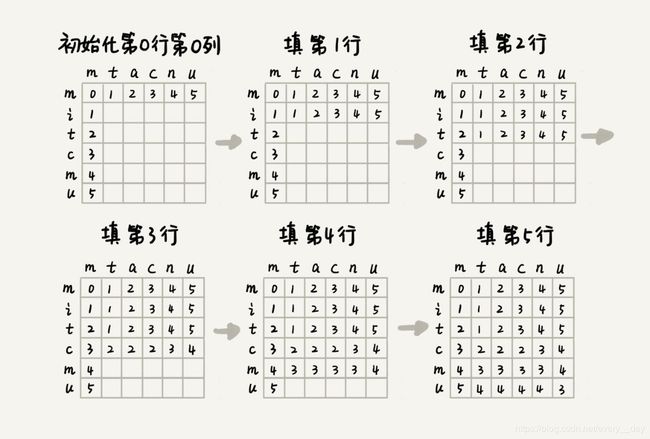
我们现在既有状态转移方程，双理清了完整的填表过程，代码实现就非常简单了。我将代码贴在下面，可对比文字看一下。

  public int lwstDP(char[] a, int n, char[] b, int m) {
    	int[][] minDist = new int[n][m];
    	for (int j = 0; j < m; j++) { // 初始化第0行，a[0..0] 与 b[0..j]的编辑距离
			if (a[0] == b[j]) {
				minDist[0][j] = j;
			}else if ( j != 0) {
				minDist[0][j] = minDist[0][j -1] + 1;
			}else {
				minDist[0][j] = 1;
			}
		}
    	for (int i = 0; i < n; i++) { // 初始化第0列：a[0..i] 与 b[0..0] 的编程距离
			if (a[i] == b[0]) {
				minDist[i][0] = i;
			} else if (i != 0) {
				minDist[i][0] = minDist[i - 1][0] + 1;
			} else {
				minDist[i][0] = 1;
			}
		}
    	for (int i = 1; i < n; i++) {
			for (int j = 1; j < m; j++) {
				if (a[i] == b[j]) {
					minDist[i][j] = min(minDist[i][j - 1] + 1, minDist[i - 1][j] + 1, minDist[i - 1][j - 1]);
				} else {
					minDist[i][j] = min(minDist[i][j - 1] + 1, minDist[i - 1][j] + 1, minDist[i - 1][j - 1] + 1);
				}
			}
		}
    	return minDist[n - 1][m - 1];
    }
    
    private int min(int x, int y, int z) {
    	int minv = Integer.MAX_VALUE;
    	if (x < minv) {
			minv = x;
		} 
    	if (y < minv) {
			minv = y;
		}
    	if (z < minv) {
			minv = z;
		}
    	return minv;
    }

你可能会说，虽然能看懂思路，但遇到新的问题，还是不知道从何下手。当我们拿到一个问题的时候，我们可以先不思考，计算机会如何实现这个问题，而是单纯考虑“人脑”会如何去解决这个问题。人脑比较倾向于思考具象化的，摸得着看得见的东西，不适合思考过于抽象的问题。所以，我们需要把抽象问题具象化。那如何具象化呢？我们可以实例化几个测试数据，通过人脑去分析具体实例的解，然后总结规律，再尝试套用学过的算法，看是否能解决。

除此之外，还有一个非常有效、但也算不上技巧的东西，也是反复强调的，要多练。实际上，等你做多了题目之后，自然就会有感觉，看问题，立马就能想到能否用动态规划解决，然后直接就可以寻找最优子结构，写出动态规划方程，然后将状态转移方程翻译成代码。

如何编程计算最长公共子串长度？

前面我们讲到，最长公共子串作为编辑距离中的一种，只允许增加、删除字符两种编辑操作。从名字上，你可能觉得看起来跟编辑距离没什么关系。实际上，从本质上说，它表征的也是两个字符串之间的相似程度。

这个问题的解决思路，跟莱文斯坦距离解决思路非常相似，也可以用动态规划解决。我刚刚已经详细讲解了莱文斯坦距离的动态规划解决思路，所以，针对这个问题，我直接定义状态，然后写状态转移方程。

每个状态还是包括三个变量（i, j, max_lcs），max_lcs 表示a[0…i] 和 b [0…j] 的最长公共子串长度。那（i, j）这个状态都是由哪些状态转移过来的呢？

我们先来看回溯的处理思路。我们从 a[0] 和 b[0] 开始，依次考察两个字符串中字符是否匹配。

• 如果 a[i] 与 b[j] 互相匹配，我们将最大公共子串长度加一，并且继续考察 a[i+1] 与 b[j+1]。
• 如果a[i] 与 b[j]不匹配，最长公共子串长度不变，这个时候，有两个不同的决策路线：
• 删除 a[i]，或者在 b[j]前面加上一个字符a[i]，然后继续考察a[i+1] 与 b[j]
• 删除 b[j]，或者在 a[i]前面加上一个字符b[j]，然后继续考察a[i] 与 b[j+1]

反过来也就是说，，如果我们要求a[0…i] 和 b [0…j]的最长公共长度 max_lcs(i, j)，我们只有可能下面三个状态转移过来

• （i-1, j-1, max_lcs），其中 max_lcs表示a[0…i-1] 和 b [0…j-1]的最长公共子串长度；
• （i-1, j, max_lcs），其中 max_lcs表示a[0…i-1] 和 b [0…j]的最长公共子串长度；
• （i, j-1, max_lcs），其中 max_lcs表示a[0…i] 和 b [0…j-1]的最长公共子串长度；

如果我们把这个转移过程，用状态方程写出来，就是下面这个样子：

• 如果：a[i] == b[j]，那么：max_lcs(i, j)就等于：max(max_lcs(i-1, j-1)+1, max_lcs(i-1, j-1), max_lcs(i-1, j-1))
• 如果：a[i] != b[j]，那么：max_lcs(i, j)就等于：max(max_lcs(i-1, j-1), max_lcs(i-1, j-1), max_lcs(i-1, j-1))
• 其中 max 表示三数中的最大值
  代码如下

   public int lcs(char[] a, int n, char[] b, int m) {
    	int[][] maxlcs = new int[n][m];
    	for (int j = 0; j < m; j++) { // 初始化第0行，a[0..0] 与 b[0..j]的maxlcs
			if (a[0] == b[j]) {
				maxlcs[0][j] = 1;
			}else if ( j != 0) {
				maxlcs[0][j] = maxlcs[0][j -1];
			}else {
				maxlcs[0][j] = 0;
			}
		}
    	for (int i = 0; i < n; i++) { // 初始化第0列：a[0..i] 与 b[0..0] 的maxlcs
			if (a[i] == b[0]) {
				maxlcs[i][0] = 1;
			} else if (i != 0) {
				maxlcs[i][0] = maxlcs[i - 1][0];
			} else {
				maxlcs[i][0] = 0;
			}
		}
    	for (int i = 1; i < n; i++) {
			for (int j = 1; j < m; j++) {
				if (a[i] == b[j]) {
					maxlcs[i][j] = max(maxlcs[i][j - 1], maxlcs[i - 1][j], maxlcs[i - 1][j - 1] + 1);
				} else {
					maxlcs[i][j] = max(maxlcs[i][j - 1], maxlcs[i - 1][j], maxlcs[i - 1][j - 1]);
				}
			}
		}
    	return maxlcs[n - 1][m - 1];
    }
    
    private int max(int x, int y, int z) {
    	int maxv = Integer.MIN_VALUE;
    	if (x > maxv) {
    		maxv = x;
		} 
    	if (y > maxv) {
    		maxv = y;
		}
    	if (z > maxv) {
    		maxv = z;
		}
    	return maxv;
    }

解答开篇

当用户在搜索框内，输入一个拼写错误的单词时，我们就拿这个意义跟词库中的单词逐一比较，计算编辑距离，将编辑距离最小的单词，作为纠正之后的单词，提示给用户。

这就是拼写纠错最基本的原理。不过真正用于商用的搜索引擎，拼写纠错功能显然不会就这么简单。一方面，单纯利用编程距离来纠错，效果并一定好；另一方面，词库中的数据量可能很大，搜索引擎每天要支持海量的搜索，所以纠错的性能要求很高。

针对纠错效果不好的问题，我们有很多种优化思路，这里介绍几种。

• 我们并不仅仅取出编辑距离最小的那个单词，而是取出编辑距离最小的 TOP10，然后根据其他参数，决策选择哪个单词作为纠错单词。比如使用搜索热门程度来决定哪个单词作为拼写纠错单词。
• 我们还可以用多种编辑距离计算方法，比如今天讲的两种，然后分别编辑距离最小的TOP10，然后求交集，用交集的结果，再继续优化处理。
• 我们还可以通过统计用户的搜索日志，得到最常被拼错的单词列表，以及对应的拼写正确的单词。搜索引擎在拼写纠错的时候，首先在这个最长被拼错单词列表中查找。如果一旦找到，直接返回对应的正确的单词。这样纠错的效果非常好。
• 我们还有更加高级一点的做法，引入个性化因素。针对每个用户，维护这个用户特有的搜索喜好，也就是常用的搜索关键词。当用户输入错误的单词的时候，我们首先在这个用户常用的搜索关键词中，计算编辑距离，查找编辑距离最小的单词。

针对纠错性能方面，我们也有相应的优化方式。我讲两种分治的优化思路

• 如果纠错功能的TPS不高，我们可以部署多台机器，每台机器运行一个独立的纠错功能。当有一个纠错请求的时候，我们通过负载均衡，分配到其中一台机器，来计算编辑距离，得到纠错单词
• 如果纠错系统的响应时间太长，也就是，每个纠错请求处理时间过长，我们可以将纠错的词库，分割到很多台机器。当有一个纠错请求的时候，我们就将这个描写错误的单词，同时发给多台机器，让多台机器并行处理，保罗得到编辑距离最小的单词，然后再比对合并，最终决定出一个最优纠错单词。

真正的搜索引擎的拼写纠错优化，肯定不上我讲的这么简单，但是万变不离其宗。掌握了核心原理，就是掌握了解决问题的方法，剩下就是自己的灵活运用和实战操作了。