tensorflow权重初始化
一,用10层神经网络,每一层的参数都是随机正态分布,均值为0,标准差为0.01
#10层神经网络
data = tf.constant(np.random.randn(2000, 800).astype('float32'))
layer_sizes = [800 - 50 * i for i in range(0, 10)]
num_layers = len(layer_sizes)
fcs = []
for i in range(0, num_layers - 1):
X = data if i == 0 else fcs[i - 1]
node_in = layer_sizes[i]
node_out = layer_sizes[i + 1]
W = tf.Variable(np.random.randn(node_in, node_out).astype('float32')) * 0.01
fc = tf.matmul(X, W)
# fc = tf.contrib.layers.batch_norm(fc, center=True, scale=True,
# is_training=True)
fc = tf.nn.tanh(fc)
fcs.append(fc)
#
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
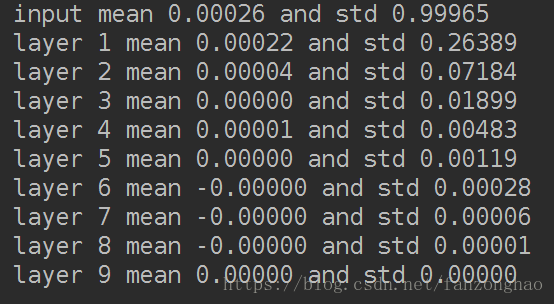
print('input mean {0:.5f} and std {1:.5f}'.format(np.mean(data.eval()),
np.std(data.eval())))
for idx, fc in enumerate(fcs):
print('layer {0} mean {1:.5f} and std {2:.5f}'.format(idx + 1, np.mean(fc.eval()),
np.std(fc.eval())))
for idx, fc in enumerate(fcs):
print(fc)
plt.subplot(1, len(fcs), idx + 1)
#绘制直方图30个bin
plt.hist(fc.eval().flatten(), 30, range=[-1, 1])
plt.xlabel('layer ' + str(idx + 1))
plt.yticks([])#把y轴刻度关掉
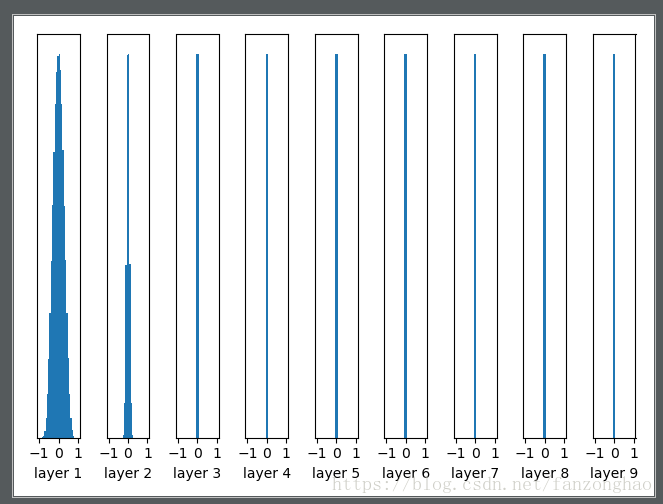
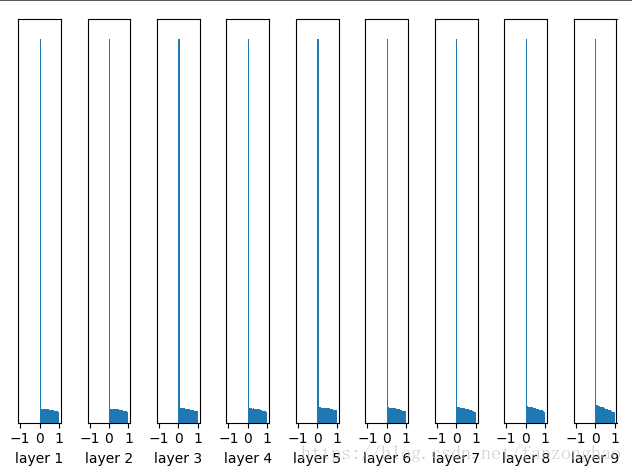
plt.show()每一层输出值分布的直方图:
随着层数的增加,我们看到输出值迅速向0靠拢,在后几层中,几乎所有的输出值 x 都很接近0!回忆优化神经网络的back propagation算法,根据链式法则,gradient等于当前函数的gradient乘以后一层的gradient,这意味着输出值 x 是计算gradient中的乘法因子,直接导致gradient很小,使得参数难以被更新!
二,标准差改为1
几乎所有的值集中在-1或1附近,神经元饱和了!注意到tanh在-1和1附近的gradient都接近0,这同样导致了gradient太小,参数难以被更新
三,Xavier initialization可以解决上面的问题!其初始化方式也并不复杂。Xavier初始化的基本思想是保持输入和输出的方差一致,这样就避免了所有输出值都趋向于0。Xavier initialization是由Xavier Glorot et al.在2010年提出,He initialization是由Kaiming He et al.在2015年提出,Batch Normalization是由Sergey Ioffe et al.在2015年提出。
#10层神经网络
data = tf.constant(np.random.randn(2000, 800).astype('float32'))
layer_sizes = [800 - 50 * i for i in range(0, 10)]
num_layers = len(layer_sizes)
fcs = []
for i in range(0, num_layers - 1):
X = data if i == 0 else fcs[i - 1]
node_in = layer_sizes[i]
node_out = layer_sizes[i + 1]
W = tf.Variable(np.random.randn(node_in, node_out).astype('float32'))/np.sqrt(node_in)
fc = tf.matmul(X, W)
# fc = tf.contrib.layers.batch_norm(fc, center=True, scale=True,
# is_training=True)
fc = tf.nn.tanh(fc)
fcs.append(fc)
#
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
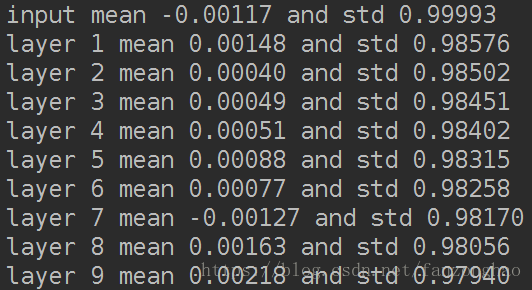
print('input mean {0:.5f} and std {1:.5f}'.format(np.mean(data.eval()),
np.std(data.eval())))
for idx, fc in enumerate(fcs):
print('layer {0} mean {1:.5f} and std {2:.5f}'.format(idx + 1, np.mean(fc.eval()),
np.std(fc.eval())))
for idx, fc in enumerate(fcs):
print(fc)
plt.subplot(1, len(fcs), idx + 1)
#绘制直方图30个bin
plt.hist(fc.eval().flatten(), 30, range=[-1, 1])
plt.xlabel('layer ' + str(idx + 1))
plt.yticks([])#把y轴刻度关掉
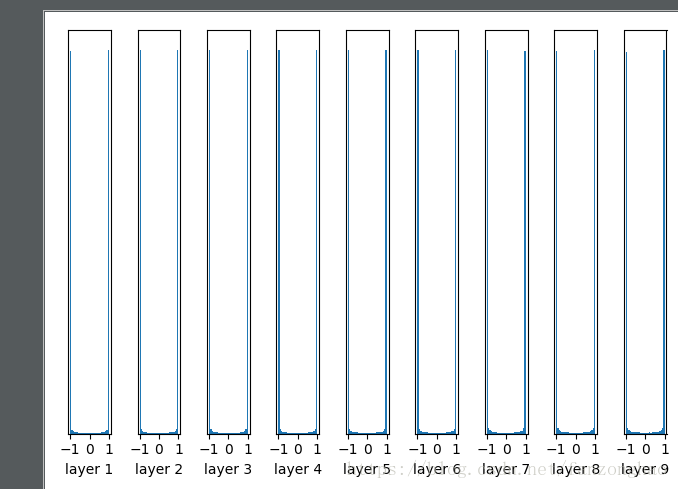
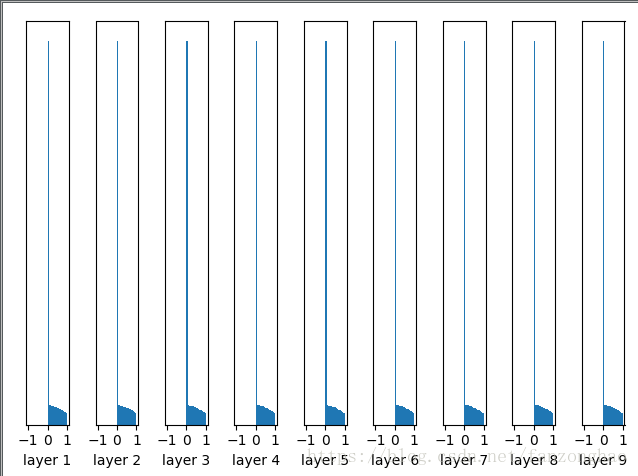
plt.show()输出值在很多层之后依然保持着良好的分布,
四,激活函数替换成relu
#10层神经网络
data = tf.constant(np.random.randn(2000, 800).astype('float32'))
layer_sizes = [800 - 50 * i for i in range(0, 10)]
num_layers = len(layer_sizes)
fcs = []
for i in range(0, num_layers - 1):
X = data if i == 0 else fcs[i - 1]
node_in = layer_sizes[i]
node_out = layer_sizes[i + 1]
W = tf.Variable(np.random.randn(node_in, node_out).astype('float32'))/np.sqrt(node_in)
fc = tf.matmul(X, W)
# fc = tf.contrib.layers.batch_norm(fc, center=True, scale=True,
# is_training=True)
fc = tf.nn.relu(fc)
fcs.append(fc)
#
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print('input mean {0:.5f} and std {1:.5f}'.format(np.mean(data.eval()),
np.std(data.eval())))
for idx, fc in enumerate(fcs):
print('layer {0} mean {1:.5f} and std {2:.5f}'.format(idx + 1, np.mean(fc.eval()),
np.std(fc.eval())))
for idx, fc in enumerate(fcs):
print(fc)
plt.subplot(1, len(fcs), idx + 1)
#绘制直方图30个bin
plt.hist(fc.eval().flatten(), 30, range=[-1, 1])
plt.xlabel('layer ' + str(idx + 1))
plt.yticks([])#把y轴刻度关掉
plt.show()前面结果还好,后面的趋势却是越来越接近0
五,He initialization的思想是:在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0,所以,要保持variance不变,只需要在Xavier的基础上再除以2:
W = tf.Variable(np.random.randn(node_in,node_out)) / np.sqrt(node_in/2)六,Batch Normalization是一种巧妙而粗暴的方法来削弱bad initialization的影响,我们想要的是在非线性activation之前,输出值应该有比较好的分布(例如高斯分布),以便于back propagation时计算gradient,更新weight。
#10层神经网络
data = tf.constant(np.random.randn(2000, 800).astype('float32'))
layer_sizes = [800 - 50 * i for i in range(0, 10)]
num_layers = len(layer_sizes)
fcs = []
for i in range(0, num_layers - 1):
X = data if i == 0 else fcs[i - 1]
node_in = layer_sizes[i]
node_out = layer_sizes[i + 1]
W = tf.Variable(np.random.randn(node_in, node_out).astype('float32'))/np.sqrt(node_in)
fc = tf.matmul(X, W)
fc = tf.contrib.layers.batch_norm(fc, center=True, scale=True,
is_training=True)
fc = tf.nn.relu(fc)
fcs.append(fc)
#
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print('input mean {0:.5f} and std {1:.5f}'.format(np.mean(data.eval()),
np.std(data.eval())))
for idx, fc in enumerate(fcs):
print('layer {0} mean {1:.5f} and std {2:.5f}'.format(idx + 1, np.mean(fc.eval()),
np.std(fc.eval())))
for idx, fc in enumerate(fcs):
print(fc)
plt.subplot(1, len(fcs), idx + 1)
#绘制直方图30个bin
plt.hist(fc.eval().flatten(), 30, range=[-1, 1])
plt.xlabel('layer ' + str(idx + 1))
plt.yticks([])#把y轴刻度关掉
plt.show()