集成学习——Boosting和Bagging
集成学习
基本思想:如果单个分类器表现的很好,那么为什么不适用多个分类器呢?
通过集成学习可以提高整体的泛化能力,但是这种提高是有条件的:
(1)分类器之间应该有差异性;
(2)每个分类器的精度必须大于0.5;
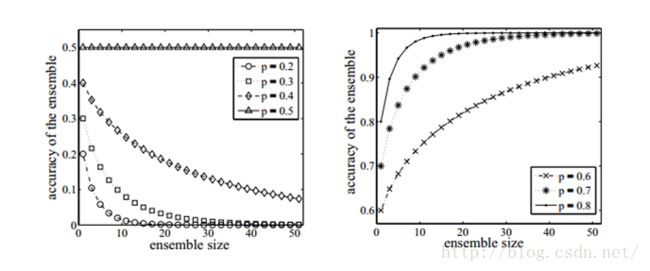
如果使用的分类器没有差异,那么集成起来的分类结果是没有变化的。如下图所示,分类器的精度p<0.5,随着集成规模的增加,分类精度不断下降;如果精度大于p>0.5,那么最终分类精度可以趋向于1。
接下来需要解决的问题是如何获取多个独立的分类器呢?
我们首先想到的是用不同的机器学习算法训练模型,比如决策树、k-NN、神经网络、梯度下降、贝叶斯等等,但是这些分类器并不是独立的,它们会犯相同的错误,因为许多分类器是线性模型,它们最终的投票(voting)不会改进模型的预测结果。
既然不同的分类器不适用,那么可以尝试将数据分成几部分,每个部分的数据训练一个模型。这样做的优点是不容易出现过拟合,缺点是数据量不足导致训练出来的模型泛化能力较差。
下面介绍两种比较实用的方法Bagging和Boosting。
Bagging(Bootstrap Aggregating)算法
Bagging是通过组合随机生成的训练集而改进分类的集成算法。Bagging每次训练数据时只使用训练集中的某个子集作为当前训练集(有放回随机抽样),每一个训练样本在某个训练集中可以多次或不出现,经过T次训练后,可得到T个不同的分类器。对一个测试样例进行分类时,分别调用这T个分类器,得到T个分类结果。最后把这T个分类结果中出现次数多的类赋予测试样例。这种抽样的方法叫做bootstrap,就是利用有限的样本资料经由多次重复抽样,重新建立起足以代表原始样本分布之新样本。
Bagging算法基本步骤:
Bagging的优势在于当原始样本中有噪声数据时,通过bagging抽样,那么就有1/3的噪声样本不会被训练。对于受噪声影响的分类器,bagging对模型是有帮助的。所以说bagging可以降低模型的方差,不容易受噪声的影响,广泛应用在不稳定的模型,或者倾向于过拟合的模型。
Boosting算法
Boosting算法指将弱学习算法组合成强学习算法,它的思想起源于Valiant提出的PAC(Probably Approximately Correct)学习模型。
基本思想:不同的训练集是通过调整每个样本对应的权重实现的,不同的权重对应不同的样本分布,而这个权重为分类器不断增加对错分样本的重视程度。1. 首先赋予每个训练样本相同的初始化权重,在此训练样本分布下训练出一个弱分类器;
2. 利用该弱分类器更新每个样本的权重,分类错误的样本认为是分类困难样本,权重增加,反之权重降低,得到一个新的样本分布;
3. 在新的样本分布下,在训练一个新的弱分类器,并且更新样本权重,重复以上过程T次,得到T个弱分类器。
通过改变样本分布,使得分类器聚集在那些很难分的样本上,对那些容易错分的数据加强学习,增加错分数据的权重。这样错分的数据再下一轮的迭代就有更大的作用(对错分数据进行惩罚)。对于这些权重,一方面可以使用它们作为抽样分布,进行对数据的抽样;另一方面,可以使用权值学习有利于高权重样本的分类器,把一个弱分类器提升为一个强分类器。
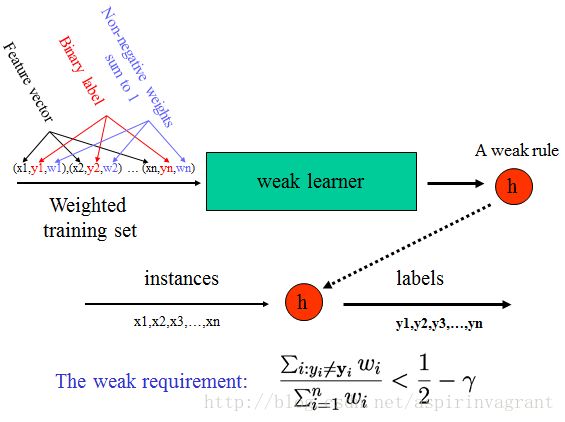
弱分类器
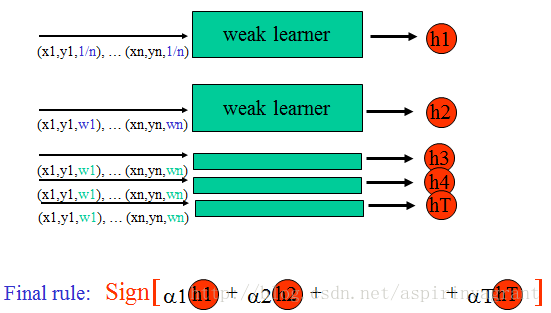
Boosting处理过程
Boosting算法通过权重投票的方式将T个弱分类器组合成一个强分类器。只要弱分类器的分类精度高于50%,将其组合到强分类器里,会逐渐降低强分类器的分类误差。
由于Boosting将注意力集中在难分的样本上,使得它对训练样本的噪声非常敏感,主要任务集中在噪声样本上,从而影响最终的分类性能。
对于Boosting来说,有两个问题需要回答:一是在每一轮如何如何改变训练数据的概率分布;二是如何将多个弱分类器组合成一个强分类器。而且存在一个重大的缺陷:该分类算法要求预先知道弱分类器识别准确率的下限。
针对上述Boosting存在的缺陷和问题,Freund和Schapire根据在线分配算法理论提出了AdaBoost算法,是一种改进的Boosting分类算法。
(1)提高那些被前几轮弱分类器线性组成的分类器错误分类的的样本的权值,这样做能够将每次训练的焦点集中在比较难分的训练样本上;
(2)将弱分类器有机地集成起来,使用加权投票机制代替平均投票机制,从而使识别准确率较高的弱分类器具有较大的权重,使其在表决中起较大的作用,相反,识别准确率较低的分类器具有较小的权重,使其在表决中起较小的作用。与Boosting分类算法相比,AdaBoost算法不需要预先获得弱分类算法识别准确率的下限(弱分类器的误差),只需关注于所有弱分类算法的分类精度(分类准确率略大于50%)。
AdaBoosting算法

训练数据:
(x1, y1), …, (xm, ym),其中 xi∈X, yi∈Y={-1, +1}
Dt(i): 样本xi在第t次迭代的权重,D1(i)=1/m
ht(X):弱分类器Ct训练得到的判别函数,ht:X->{-1, +1}
εt:ht(X)的错误率,加权分类误差(weighted error)
αt:分类器的系数,根据误差计算,误差越小,权重越大
上面权重Dt+1(i)的更新是基于前一步的权重Dt(i),而非局域全局更新。
AdaBoost分类算法是一种自适应提升的方法,由于训练的过程是重复使用相同的训练集,因而不要求数据集很大,其自身就可以组合任意数量的基分类器。在AdaBoost算法中,尽管不同的基分类器使用的训练集稍有差异,但这种差异是随机选择造成的,所不同的是,这种差异是前一个基分类器的误差函数。而提升的过程是针对一个特定问题的实际性能,显然这就依赖于具体的数据和单个基分类器的性能。因此,训练的过程需要有充足的训练数据,并且基分类器应当是弱的但又不至于太弱(即分类准确率略大于50%),而提升的过程对噪声和离群点的干扰尤为明显。
Boosting与Bagging的不同之处:
1、Bagging的训练集是随机的,以独立同分布选取的训练样本子集训练弱分类器,而Boosting训练集的选择不是独立的,每一次选择的训练集都依赖于上一次学习的结果,根据错误率取样,因此Boosting的分类精度在大多数数据集中要优于Bagging,但是在有些数据集中,由于过拟合的原因,Boosting的精度会退化。
2、Bagging的每个预测函数(即弱假设)没有权重,而Boosting根据每一次训练的训练误差得到该次预测函数的权重;
3、Bagging的各个预测函数可以并行生成,而Boosting的只能顺序生成。
4、Bagging是减少variance,而Boosting是减少bias。
参考资料:
Ensemble methods. Bagging and Boosting
Bagging, boosting and stacking in machine learning
HITSCIR-TM zkli-李泽魁 Bagging & Boosting