TensorFlow——CNN实现MNIST手写体识别

TensorFlowCNN实现MNIST

官方文档 —— MNIST 入门 | Softmax 相关
官方文档 —— MNIST 进阶 | CNN 相关
CNN-卷积神经网络相关

---

1，数据集

MNIST是一个入门级的计算机视觉数据集，它包含各种手写数字图片：

这份Python代码是官方网站上提供给我们下载和安装数据集的，然后可以使用下面的代码导入到你的项目里面：

import input_data
mnist = input_data.read_data-sets("MNIST_data/", one_hot=True)

下载下来是一个60000行的训练数据集（mnist.train）和一个10000行的测试数据集（mnist.test）。
数据集的每个数据单元包含：

• 一张手写数字的图片（28x28=784）
• 对应的标签[1x10]

在训练数据集中，mnsit.train.images是一个形状为[60000, 784]的一个张量，第一个维度是图片索引也就是样本序号，第二个维度是图片像素点，也就是相对于每张28x28=784的图片转换为一个1x784的向量来处理，总共是60000x784。

对用的标签是介于0到9的数字，用一个向量表示，例如0的标签为：[1, 0, 0, 0, 0, 0, 0, 0, 0, 0]，也就是第0位为1，其他为0的1x10的向量，来表示标签0。因此mnist.train.labels是一个[60000, 10]的张量

2，回归模型——Softmax

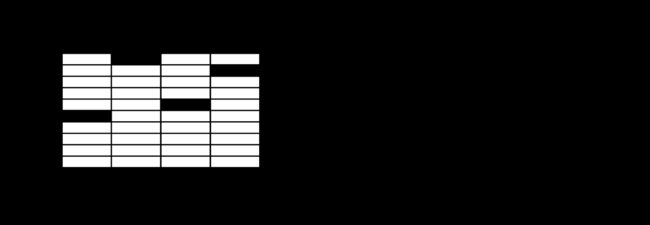
我们针对每个数字，给出每个数字对应的28x28=784个像素不同的权值，与这个数字相关程度较大的像素，我们给予相对更高的权重（正值），反之给予较低的权重（负值），如下图所示，红色为负值，蓝色为正值，黑色表示我们对这部分像素不关心：

对每一张图片，根据相应的数字 $i$ 所对应的每个像素$x_j$的权重$W_{i,j}$，求出乘积和在加上一个偏置量（因为输入往往会有干扰），得到一个证据值，它描述的是我们能够认为这张图片是对应数字 $i$ 的把握的大小：
$$evidenc{e}_i=\sum _j{W}_{i,j}{x}_j+b_i\text{\hspace{1em}(0)}$$
我们更希望得到的是这张图片关于0-9每个数字的概率分布。我们通过softmax这个激励函数把这个证据量转化为对应数字 $i$ 一个概率值$y_i$：
$$y_i=softmax(evidenc{e}_i)\text{\hspace{1em}(1)}$$
可以这样定义函数softmax：
$$softmax(x)=normalize(exp(x))\text{\hspace{1em}(2)}$$
右边具体展开如下：
$$softmax(x{)}_i=\frac{exp(x_i)}{{\sum }_{j}exp(x_j)}\text{\hspace{1em}(3)}$$
我们可以使用下图来表示一个softmax回归模型：

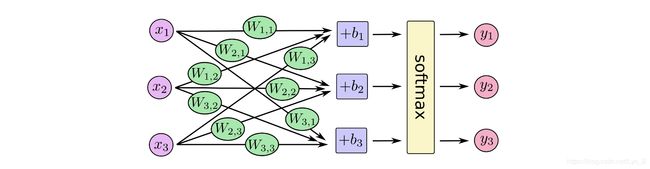
写成等式如下：

用矩阵相乘的方法可以优化计算效率（例如，权重矩阵相乘再和输入层作运算可以减少运算量）：

最终我们可以用下面表示，其中$x$是输入向量，$b$是偏置向量，$y$是输出向量：
$$y=softmax(Wx+b)\text{\hspace{1em}(4)}$$

3，卷积神经网络 Convolutional Neural Network - CNN

下图展示了底层几乎一模一样的简单特征（如简单的线段，曲线，边缘等），通过组合成为各不相同的高级特征，最终组合成不同内容的图像：

卷积神经网络的目的就是：通过提取底层特征，接着根据较低层的特征识别出较为高级的特征，通过多层的特征提取，最终识别出图像的具体内容。
卷积神经网络的两个核心过程是：

• 卷积 Convolution
• 池化 Pooling

卷积 Convolution

卷积操作如下图所示：

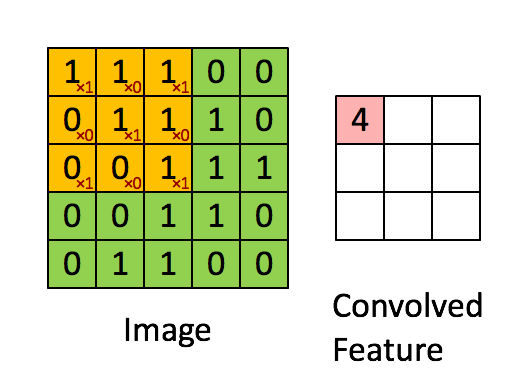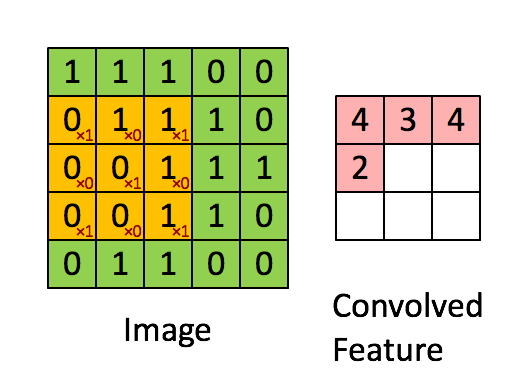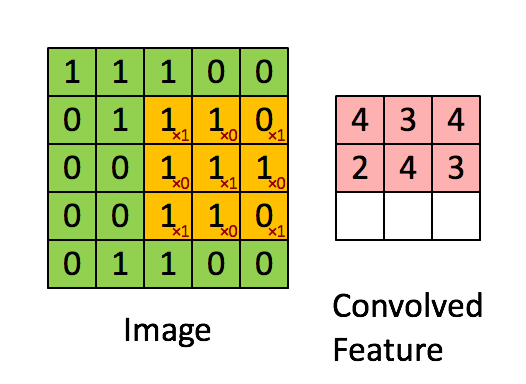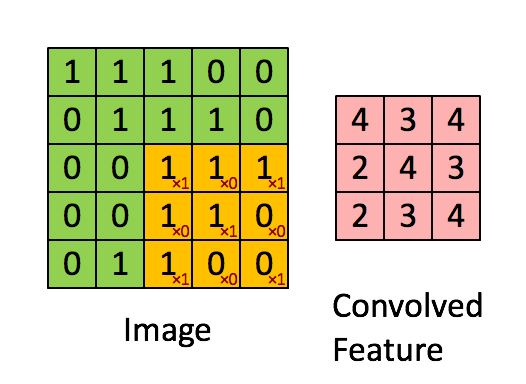
用于卷积的模板是我们所关注的特征，我们认为局部的$n\times n$的像素块可以描述这样的特征，我们通过用这个特征作为模板对图像进行卷积操作，来得到图像局部位置和特征的相关性，得到的结果如上图所示，就是一个卷积特征矩阵。一般会针对多个特征设计多个卷积模板，例如下面的24个特征对应的模板：

池化 Pooling

池化过程如下：

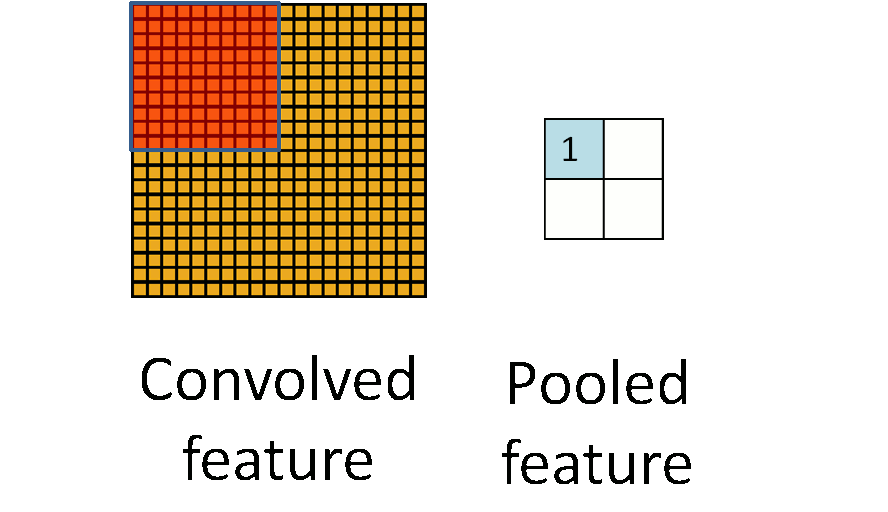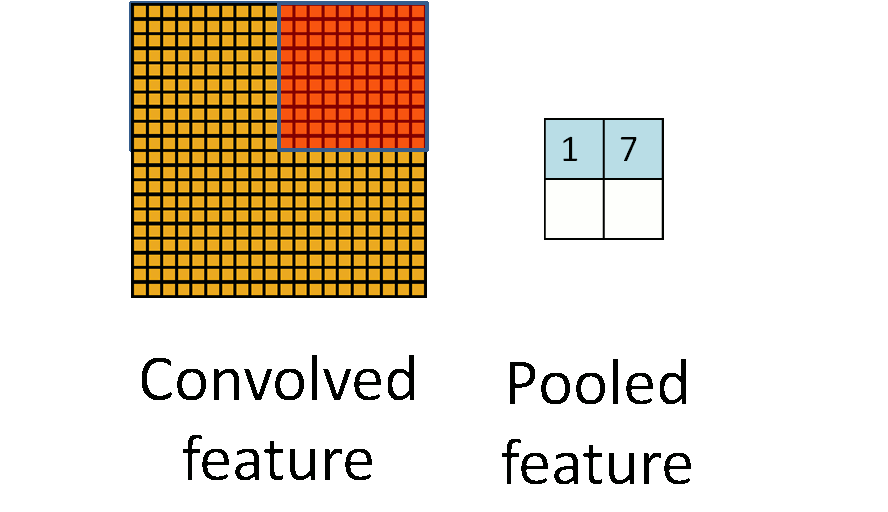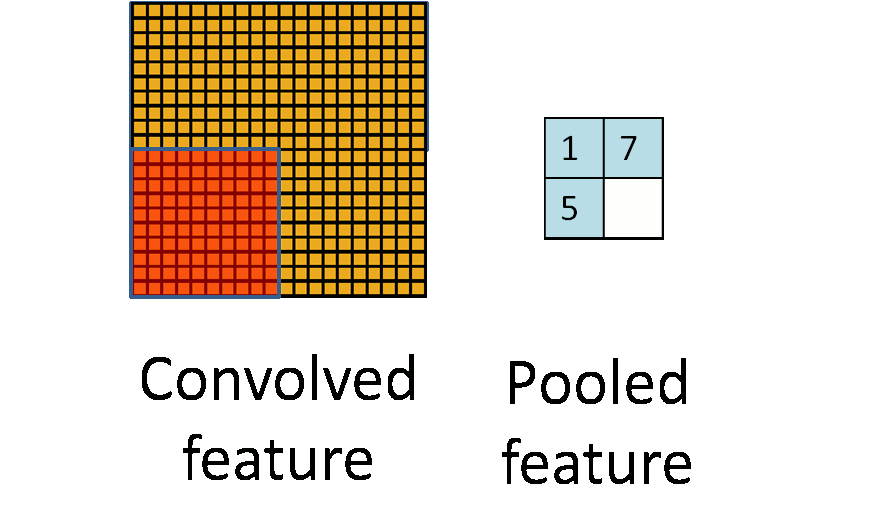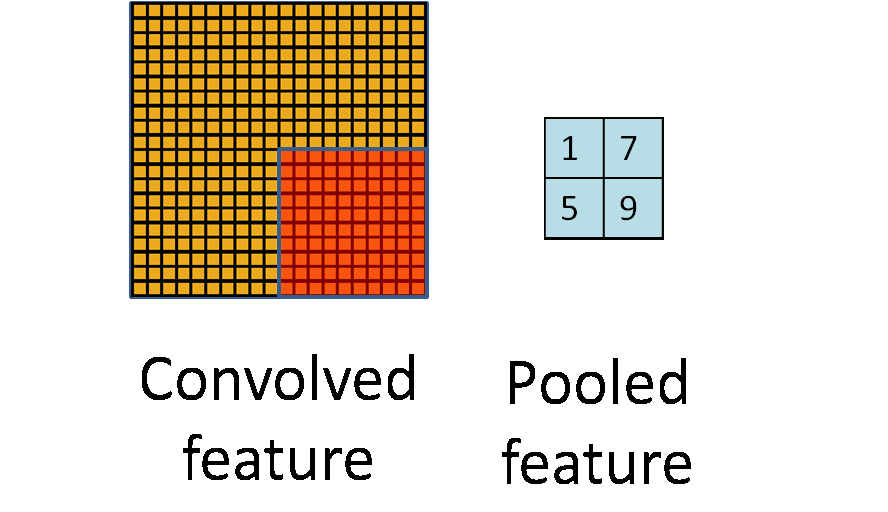
事实上，可以看到，所谓的池化就是一个下采样（subsampling）的过程，将卷积特征图像下采样为池化特征图像。
由于卷积过程中卷积核相对于图像来说过小，所以卷积得到的图像结果依然非常大，所以我们希望进行一个下采样来减少数据的维度，并且降低过拟合。
这是基于特征的统计特性依然能够很好的描述图像的特征这一特点，使得我们可以通过提取特征的统计特性来减少数据维度，常用的有：

• 平均值下采样
• 最大值下采样

卷积神经网络结构

希望构建的CNN（Convolution Neural Network 卷积神经网络）结构如下：

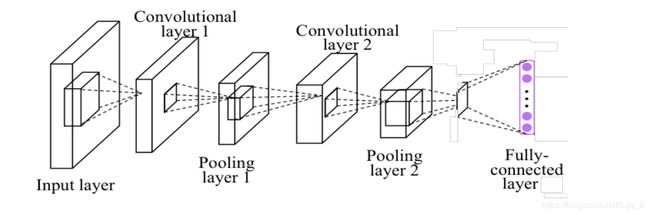
• Input layer 输入层
• Convolutional layer 1 卷积层1
• Pooling layer 1 池化层1
• Convolutional layer 2 卷积层2
• Pooling layer 2 池化层2
• Fully-connected layer 密集连接层

函数定义

首先定义权重和偏置量初始化函数：

权重初始化

# for weights intialization
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

tf.truncated_normal函数是在截断正态分布中随机选取一个值，其中shape是生成的张量的维度，stddev是正态分布的标准差，mean均值默认为 $0$

偏置量初始化

# for biases initialization
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

这个模型中的权重在初始化时应该加入少量的噪声来打破对称性以及避免0梯度。由于我们使用的是ReLU神经元，因此比较好的做法是用一个较小的正数来初始化偏置项，以避免神经元节点输出恒为0的问题（dead neurons）。

接下来定义卷积函数和池化函数。

卷积函数

卷积过程关键在于：

• 边界处理
• 步长设置

我们定义了一个二维卷积函数：

def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

其中，$x$为卷积图像，$W$为卷积模板，另外两个参数决定了我们将怎样进行卷积：

• strides：这是一个四维的向量，但是决定我们水平和垂直移动模板的只是中间的两个参数，这里我们设置步长为1，即[1, 1, 1, 1]
• padding：这个参数决定了我们的补0方式，参数值为${}^{\prime }sam{e}^{\prime }$表示关于模板对称补0，也就是最终输出的结果大小将会和原图像一样大

这样我们保证了输出和输入的大小相同。

池化函数

池化我们采用简单的$2\times 2$的池化模板进行最大值下采样（max pooling）：

def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

参数strides：可以看到这里的四维向量步长为$[1,2,2,1]$，即水平步长为2，垂直步长也为2，也就是每$2\times 2=4$个值保留其中最大值，实现了下采样。

3.1，Input layer 输入层

我们从MNIST数据集中读入数据，并创建两个用于输入数据（图片数据和对应的标签数据）的结点：

import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

# images data
x = tf.placeholder("float", shape=[None, 784])
# images labels
y_ = tf.placeholder("float", shape=[None, 10])

这里 $x$ 和 $y\_$ 不是两个变量，而是定义为两个占位符，这是为了方便让我们可以输入不同数量的图片，采用占位符设置第一维维$None$，允许输入的张量的第一维为任意大小。
我们采用随机采样 $n$ 个训练样本进行训练，后面我们使用 $batch$ 表示本次训练批次中样本的数量。

3.2，Convolutional layer 1 卷积层1

进入第一层的卷积操作。
首先，定义两个变量：
W_conv1：第一层卷积的权重，前两个是模板大小参数，第三个参数是输入的通道数，最后一个参数是输出的通道数。通过这个$5\times 5$的模板对$28\times 28$的图像进行卷积计算出$32$个特征值，即，我们用$32$个模板对每一张图片进行卷积得到这张图片对应这$32$个特征的特征值
b_conv1：第一层卷积的偏置量，每一个输出通道对应一个偏置量

# first layer's weights and biases
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])

为了在这一层进行卷积操作，对输入层的数据进行$reshape$：
$$[batch,784]\Rightarrow [batch,28,28,1]\text{\hspace{1em}(5)}$$

# reshape from 784x1 to 28x28
x_image = tf.reshape(x, [-1,28,28,1])

得到的x_image是一个4维的向量：

• 第1维为-1，表示自动得到这一维的大小，也就是我们这一批随机样本的个数 $batch$
• 第2，3维为宽和高，即手写数字图像的大小$28\times 28$
• 第4维为通道数，我们这里是灰度图像，所以通道数量为1，如果为RGB图像，通道数量为3

调用函数conv2d进行卷积操作，然后加上偏置向量，应用ReLU激励函数：

# Convolutional 1
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)

最终我们得到的输入到输出的转换结果为：
$$[batch,28,28,1]\Rightarrow [batch,28,28,32]\text{\hspace{1em}(6)}$$
即这张图片对应的$32$个特征图像

3.3，Pooling layer 1 池化层1

接下来进入第一层的池化操作，对第一层卷积层得到的卷积结果进行max_pooling：

# Pooling 1
# subsample from 28x28 to 14x14
h_pool1 = max_pool_2x2(h_conv1)

得到降维后的结果h_pool1，此时宽和高从$28\times 28$变为了$14\times 14$:
$$[batch,28,28,32]\Rightarrow [batch,14,14,32]\text{\hspace{1em}(7)}$$

3.4，Convolutional layer 2 卷积层2

定义第二层卷积层的权重和偏置量：
W_conv2：在这一层中我们同样采用$5\times 5$的模板进行卷积，但是这里输入的通道数是上一层输出的通道数量，即$32$个特征值，输出为64个更高级的特征

# second layer's weights and biases
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])

我们可以结合神经网络的知识来理解：
在下一层的隐藏层中有64个神经元，这一层的32个神经元对下一层的每一个神经元都有 一个输入，并且对应有一个权重（实际上对于图像处理，在二维空间里，这里是一个卷积模板），并且这一层的每个神经元对于下一层的每个神经元的输入权重是不同的（通常来说）。
对于下一层的神经元的输出，将会是上一层的每个神经元的输入和对应权重的乘积和，在这里是对应的卷积结果得到的图像相加，下一层隐藏层第 $i$ 个神经元的输出写成：
$$P_i=\sum _j{W}_{j,i}{x}_j\text{\hspace{1em}(8)}$$
其中$W_{j,i}$是对应上一层第 $j$ 个神经元的卷积模板，$x_j$ 为第 $j$ 个神经元到这个神经元的输入，再结合激励函数：
$$Outpu{t}_i=ReLU(P_i)\text{\hspace{1em}(9)}$$
最终进行卷积运算的代码如下，事实上只是改变了输入权重和偏置量：

# Convolutional 2
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)

这一层卷积得到的输入到输出的转换为：
$$[batch,14,14,32]\Rightarrow [batch,14,14,64]\text{\hspace{1em}(10)}$$

3.5，Pooling layer 2 池化层2

同样我们采用简单的$2\times 2$的池化模板进行最大值下采样（max pooling）：

# Pooling 2
# subsample from 14x14 to 7x7
h_pool2 = max_pool_2x2(h_conv2)

这一层输入到输出的转换为：
$$[batch,14,14,64]\Rightarrow [batch,7,7,64]\text{\hspace{1em}(11)}$$

3.6，Fully-connected layer 密集连接层

到这里，图片尺寸已经缩小到了 $7\times 7$ ，我们加入一个有 $1024$ 个神经元的密集连接层来处理整张图片。

# Fully connected
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])

可以看到，密集连接层的权重第一个维度的大小和第二个池化层神经元输出结果的大小相同，这样我们接下来对池化层的结果进行 $reshape$ 的话：

h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])

再进行矩阵乘法：

h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

最终我们将会把每张图片提纯成一个$[1,1024]$的向量，最终实现的转换为：
$$[batch,7,7,64]\Rightarrow [batch,1024]\text{\hspace{1em}(12)}$$
这样高度提纯的特征可以方便我们后面进行分类回归

3.7，dropout

dropout的思想是，让一些神经元以某个概率 $p$ 随机将激活值置为 $0$，停止工作，如下图所示：

这样可以防止对某一个特征过度依赖，降低模型的过拟合程度，提高模型的泛化性。
下面的代码实现了 $dropout$：

# dropout
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

TensorFlow函数tf.nn.dropout的作用为：

• 使得输入矩阵，如h_fc1，中的元素随机变为0，概率大概为输入参数keep_prob
• 其余的元素的值变为element/keep_prob

变为 $0$ 的输出相当于我们所丢弃掉的结点，这样在每次迭代完之后，都会更新我们的卷积神经网络，使得新的一部分结点在新的迭代中将会被 $drop$ 掉，由此就实现了 $dropout$ 过程。

3.8，Softmax

最终根据前面密集连接层的 $1024$ 个神经元的输出和权重的乘积和得到对应 $0$ 到 $9$ 每个数字的证据量，然后通过tf.nn.softmax函数转换为相应的概率分布：

# output with softmax regression
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])

y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

3.9，training and evaluating 训练和评估

我们需要定义一个指标来评价我们的模型质量，这样才能有助于我们训练模型，这个指标就是我们常说的成本（cost）或者是损失（loss），然后通过最小化这个指标来达到我们训练的目的。
我们通过一个成本函数——“交叉熵”（Cross Entropy）来判断一个模型的好坏：
$$H_{y^{\prime }}(y)=-\sum _i{y}_i^{\prime }log(y_i)\text{\hspace{1em}(13)}$$
其中，$y$ 是我们预测得到的概率分布，而$y^{\prime }$是实际的概率分布，代码如下：

# get cross entropy
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))

使用 $Adam$ 优化器通过最小化交叉熵进行步长优化：

train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

解析来通过tf.equal来比较我们的识别结果，argmax将会得到概率最大值的标签，通过比较这两个标签，判断识别正确与否：

correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))

最终将会得到一组布尔值，然后通过下面的函数：

accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

将会把这一组布尔值转化为一组浮点数，例如:
$$[TrueFalseTrueTrue]\Rightarrow [1.00.01.01.0]\text{\hspace{1em}(14)}$$
然后取平均值将会得到我们最终想要的识别正确率，例如上面将会得到正确率为 $75\%$。
最后，我们开始运行我们的模型：

sess.run(tf.initialize_all_variables())
# sess.run(tf.global_variables_initializer())
for i in range(20000):
	# 50一批
	batch = mnist.train.next_batch(50)
	# 每100次迭代输出日志
	if i%100 == 0:
		train_accuracy = accuracy.eval(
			feed_dict={
				x:batch[0], 
				y_: batch[1], 
				keep_prob: 1.0
			})
		print("step %d, training accuracy %g"%(i, train_accuracy))
	# 训练
	train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
# 输出最终得到的准确率
print("test accuracy %g"%accuracy.eval(
	feed_dict={
		x: mnist.test.images, 
		y_: mnist.test.labels, 
		keep_prob: 1.0
		}))

4，运行

完整代码如下：

import tensorflow as tf
import input_data


# for weights intialization
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)
# for biases initialization
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

# convolution
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

# pooling
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

# start graph
sess = tf.InteractiveSession()

# read data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

# images data
x = tf.placeholder("float", shape=[None, 784])
# images labels
y_ = tf.placeholder("float", shape=[None, 10])

# first layer's weights and biases
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])

# reshape from 784x1 to 28x28
x_image = tf.reshape(x, [-1,28,28,1])

# Convolutional 1
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)

# Pooling 1
# subsample from 28x28 to 14x14
h_pool1 = max_pool_2x2(h_conv1)


# second layer's weights and biases
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])

# Convolutional 2
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
# Pooling 2
# subsample from 14x14 to 7x7
h_pool2 = max_pool_2x2(h_conv2)


# Fully connected
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])

h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# dropout
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

# output with softmax regression
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])

y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)


# training and evaluating
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess.run(tf.initialize_all_variables())
# sess.run(tf.global_variables_initializer())
for i in range(20000):
	# 50一批
	batch = mnist.train.next_batch(50)
	# 每100次迭代输出日志
	if i%100 == 0:
		train_accuracy = accuracy.eval(
			feed_dict={
				x:batch[0], 
				y_: batch[1], 
				keep_prob: 1.0
			})
		print("step %d, training accuracy %g"%(i, train_accuracy))
	# 训练
	train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
# 输出最终得到的准确率
print("test accuracy %g"%accuracy.eval(
	feed_dict={
		x: mnist.test.images, 
		y_: mnist.test.labels, 
		keep_prob: 1.0
		}))

结果：
这里截取前面几个日志（因为每100步输出一行日志所以总共有200行日志）：

最终结果：

训练得到的模型识别正确率为 $99.27\%$