算法与数据结构之美-链表
算法与数据结构之美-链表
- 开篇思考
- 五花八门的链表结构
- 单链表
- 循环链表
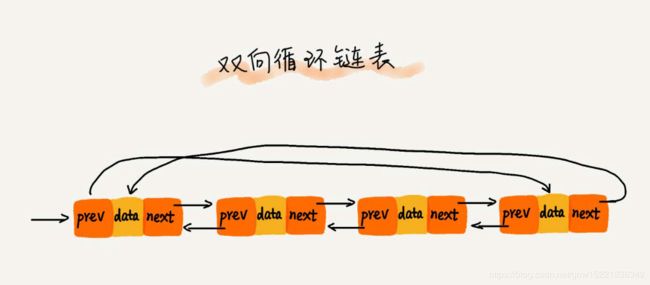
- 双向链表
- 链表VS数组
- 解答开篇
- 代码
- 参考
开篇思考
链表有一个经典的应用场景,就是LRU缓存淘汰算法,常见的缓存淘汰算法有:
先进先出FIFO、最少使用LFU、最近最少使用策略LRU
思考一下:如何用链表实现LRU缓存淘汰策略?
五花八门的链表结构
数组需要一块连续的内存空间来存储,对于内存的要求比较高,假如需要100MB大小的内存空间,但是内存中没有连续的100MB空间,即便剩余的总空间大于100MB,也会申请失败。
链表恰恰相反,并不需要一块连续的内存空间,可以通过“指针”将一组零散的内存块串联起来使用。
本文主要介绍:单链表、双向链表、循环链表
单链表
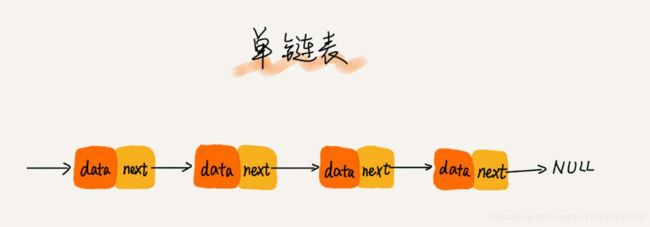
第一个结点是头结点,用来记录链表的基地址,有了它就可以遍历整条链表。最后一个结点是尾结点,它指向的下一个结点是一个NULL。与数组一样,链表也支持数据的查找、插入和删除。
与数组不同的是,链表在进行插入和删除的时候不需要为了保持内存的连续性而搬移结点,只需要考虑相邻结点的指针变化,时间复杂度为O(1)。但是,链表就不能随机访问第K个元素,需要根据指针依次遍历,直到找到相应的结点。所以,链表随机访问的时间复杂度是O(n)。
循环链表
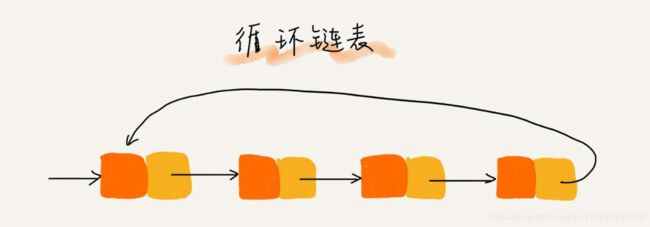
循环链表是一种特殊的单链表,唯一的区别就是循环链表的尾结点,指向链表的头结点。在处理环形问题时,就适合采用循环链表,例如约瑟夫环。
双向链表
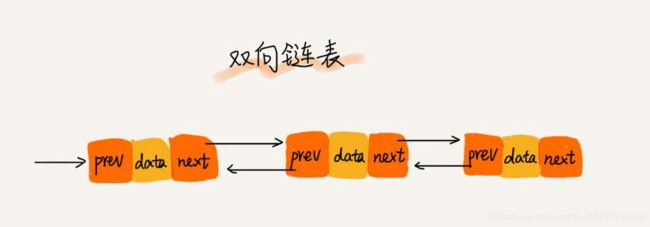
双向链表需要额外的两个空间来存储前驱节点和后继结点的指针。相比于单链表,要占用较多的内存空间,但是支持双向遍历,为双向链表的操作带来了灵活性。
实际软件开发中,链表删除一个数据主要是两种情况:
- 删除结点中“值等于某个给定值”的结点
- 删除给定指针指向的结点
第一种情况,单双链表删除的时间复杂度都是O(1),但是遍历查找比较费时间,对应的时间复杂度是O(n)。
第二种情况,已经遍历到了需要删除的结点,但是删除结点,需要知悉其前驱结点p,单链表不支持前驱结点,还需要从头开始遍历查找其前驱结点,双链表就不需要再次遍历,只需要在O(1)的时间复杂度内解决。
同理删除操作也是相同的,对于有序链表,双向链表按值查询的效率较高。可以根据上次查询的结点P,来判断是向前还是向后查找。
实际开发中,双向链表比较占用内存,但是比单链表应用更加广泛,例如LinkedHashMap其中就用到了双向链表。
当内存空间充足时,为了追求代码的执行效率,可以考虑采用空间换时间的方式。缓存技术就是利用了空间换时间设计思想,事先将数据加载到内存中,虽然耗费内存,但是大大提升了数据的访问速度。
链表VS数组
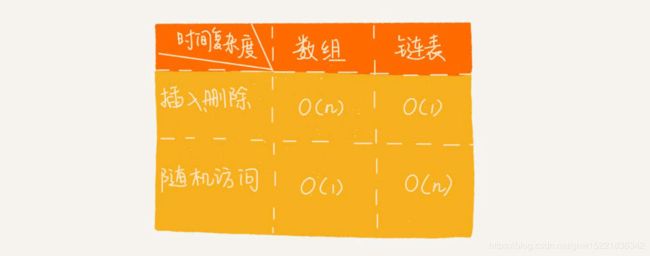
在实际开发中,不能仅仅根据复杂度分析来决定使用哪个数据结构:
数组简单易用,需要分配连续的内存空间,借助CPU的缓存机制,预读数组中的数据,所以访问效率高,链表不是连续存储的,对于CPU的缓存不友好,不能预读;
链表不需要分配空间,可以支持动态扩容;
针对于不同的项目,需要权衡采用数组还是链表。
解答开篇
采用单链表实现LRU算法:
维护一个单链表,越靠近链表尾部的就是越早之前访问的,当访问新的数据时,从链表头开始遍历链表:
-
如果链表之前存在该数据,遍历得到该结点并删除,再插入到链表的头部;
-
如果链表没有该数据,就分为两种情况:
- 此时缓存未满,将此结点插入链表头部;
- 若缓存已满,就删除链表的尾结点,再将数据插入到链表头部;
代码
public class LRUBaseLinkedList<T>{
private final static Integer DEFAULT_CAPACITY = 10; //默认链表容量
private SNode<T> headNode; //头结点
private Integer length; //链表长度
private Integer capacity; //链表容量
public LRUBaseLinkedList(Integer capacity){
this.headNode = new SNode<>();
this.capacity = capacity;
this.length = 0;
}
public LRUBaseLinkedList(){
this.headNode = new SNode<>();
this.capacity = DEFAULT_CAPACITY;
this.length = 0;
}
public void add(T data){
SNode preNode = findPreNode(data);
//链表中存在,就删除原数据,插入链表头部
if(preNode!=null){
deleteNode(preNode);
insertNodeAtBegin(data);
}else{
if(length>=this.capacity){
deleteNodeAtEnd();
}
insertNodeAtBegin(data);
}
}
//查找元素的前一个结点
private SNode findPreNode(T data){
SNode node = headNode;
while(node.getNext() != null){
if(data.equals(node.getNext().getElement())){
return node;
}
node = node.getNext();
}
return null;
}
//删除元素
private SNode deleteNode(SNode preNode){
SNode temp = preNode.getNext();
preNode.setNext(temp.getNext());
temp = null;
length--;
}
//删除末尾的元素
private SNode deleteNodeAtEnd(){
SNode node = headNode;
//空链表直接返回
if(node.getNext()==null)
return;
//倒数第二个结点
while(node.getNext().getNext()!=null){
node = node.getNext();
}
SNode temp = node.getNext();
node.setNext(null);
tmp = null;
length--;
}
private void printAll(){
SNode node = headNode.getNext();
while(node!=null){
System.out.println(node.getElement()+“,”);
node = node.getNext();
}
System.out.println();
}
public class SNode<T>{
private T element;
private SNode next;
public SNode(T element) {
this.element = element;
}
public SNode(T element, SNode next) {
this.element = element;
this.next = next;
}
public SNode() {
this.next = null;
}
public T getElement() {
return element;
}
public void setElement(T element) {
this.element = element;
}
public SNode getNext() {
return next;
}
public void setNext(SNode next) {
this.next = next;
}
}
publlic static void main(String[ ] args){
LRUBaseLinkedList list = new LRUBaseLinkedList();
Scanner sc = new Scanner(System.in);
while(true){
list.add(sc.nextInt());
list.printAll();
}
}
}
参考
[1] 极客时间-数据结构与算法之美-链表(上)