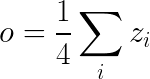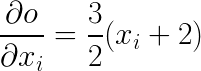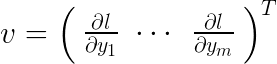基于PyTorch的深度学习入门教程_autograd_tutorial

摘要

Autograd:自动分化
PyTorch中所有神经网络的核心是“autograd”包。
让我们先简单地看一下这个，然后我们来训练我们的第一个神经网络。

“autograd”包为张量上的所有操作提供自动微分。它是一个按运行定义的框架，这意味着您的支持是由代码的运行方式定义的，并且每个迭代都可以是不同的。

让我们用更简单的术语和一些例子来看看。

张量

"torch.Tensor'"是包的中心类。如果您设置了它的属性
".requires_grad"作为"True"，它开始跟踪它上面的所有操作。当您完成计算时，您可以调用' ' .backwards() ' '并自动计算所有的梯度。这个张量的梯度将累积为".grad"属性。

要阻止张量跟踪历史，可以调用' ' .detach() ' '来进行分离它从计算的历史，并防止未来的计算存在跟踪。

为了防止跟踪历史(和使用内存)，还可以包装代码块“with torch.no_grad (): ' '。这在评估模型时特别有用，因为模型可能具有可训练的参数‘requires_grad=True’，但是对于这些参数，我们不需要梯度。

还有一个类对autograd的实现非常重要——一个“函数”。

“张量”和“函数”是相互联系的，并建立一个非循环图，它编码了一个完整的计算历史。每个张量都有一个' '.grad_fn ' '属性引用一个' '函数' ' '创建了' '张量' '(用户创建的张量除外——他们的' ' grad_fn是None ' ')。

如果你想计算导数，你可以在张量上调用' '.backward()' '。如果‘张量’是一个标量(即它包含一个元素数据)，你不需要为‘backward()’指定任何参数，但是如果它有更多的元素，你需要指定一个‘梯度’参数，它是一个形状匹配的张量。

import torch

###############################################################
# Create a tensor and set ``requires_grad=True`` to track computation with it
x = torch.ones(2, 2, requires_grad=True)
print(x)

###############################################################
# Do a tensor operation:
y = x + 2
print(y)

###############################################################
# ``y`` was created as a result of an operation, so it has a ``grad_fn``.
print(y.grad_fn)

###############################################################
# Do more operations on ``y``
z = y * y * 3
out = z.mean()
print(z, out)

################################################################
# ``.requires_grad_( ... )`` changes an existing Tensor's ``requires_grad``
# flag in-place. The input flag defaults to ``False`` if not given.
a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

###############################################################
# Gradients
# ---------
# Let's backprop now.
# Because ``out`` contains a single scalar, ``out.backward()`` is
# equivalent to ``out.backward(torch.tensor(1.))``.

out.backward()
###############################################################
# Print gradients d(out)/dx
print(x.grad)

输出结果： 

•  tensor([[1., 1.],
          [1., 1.]], requires_grad=True)
  tensor([[3., 3.],
          [3., 3.]], grad_fn=)
  
  tensor([[27., 27.],
          [27., 27.]], grad_fn=) tensor(27., grad_fn=)
  False
  True
  
  tensor([[4.5000, 4.5000],
          [4.5000, 4.5000]])

原理如下： 

向量-雅可比矩阵(雅可比矩阵定义为向量对向量的微分矩阵)乘积原理：

      

 给出了一个行向量，该行向量可以作为列向量来处理   

#向量-雅可比矩阵乘积的这种特性使得将外部梯度输入具有非标量输出的模型非常方便。
# Now let's take a look at an example of vector-Jacobian product:

x = torch.randn(3, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

###############################################################
# Now in this case ``y`` is no longer a scalar. ``torch.autograd``
# could not compute the full Jacobian directly, but if we just
# want the vector-Jacobian product, simply pass the vector to
# ``backward`` as argument:
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)

###############################################################
#你也可以停止autograd从跟踪张量的历史，该张量带有requires_grad=True通过torch.no_grad()方法将代码块封装。
print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)

###############################################################
# **Read Later:**
#
# Documentation of ``autograd`` and ``Function`` is at
# https://pytorch.org/docs/autograd

输出结果如下： 

tensor([-995.4692,  -19.2571,  808.9395], grad_fn=)
tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])
True
True
False

链接地址：https://github.com/pytorch/tutorials/tree/master/beginner_source/blitz