CUDA编程—通过shared memory优化矩阵相乘

1、矩阵乘的CPU代码

下面的所有均亲自测试，可直接运行

#include 
using namespace std;

void MatrixMulOnHost(int m, int n, int k, float* A, float* B, float* C)
{
    for (int Row = 0; Row < m; ++ Row)
		for (int Col = 0; Col < k; ++ Col )
		{
			float sum = 0;
			for (int i = 0; i < n; ++i)
			{
				float a = A[Row * n + i];
				float b = B[Col + i * k];
				sum += a * b;
			}
			C[Row* k + Col] = sum;
		}
}

int main()
{
	//这里将矩阵按照行优先转换成了一维的形式
	float A[6] = { 11.4, 24, 33.5,   45, 55 ,32.4 }; //2×3的矩阵
	float B[12] = {12,43,22.4, 31.3,  12,324,23,12,  44.4,23.4,65.3,73};//3×4的矩阵
	float C[8] = { 0 }; //2×4的结果矩阵
	int m=2,n=3,k=4;

	MatrixMulOnHost(m, n, k, A, B, C);

	//输出结果
    for (int i=0;i<8;i++)
	{
		cout<

2、矩阵乘的GPU代码--体会SIMT的思想

体会：首先考虑其中的一个thread是如何实现指令的，然后考虑如何进行并行化处理的。

#include "cuda_runtime.h"
#include "device_launch_parameters.h"

#include 
using namespace std;

cudaError_t addWithCuda(int *c, const int *a, const int *b, unsigned int size);

__global__ void MatrixMulKernle(int m, int n, int k, float *A,float  *B, float *C)
{
	int Row=blockIdx.y*blockDim.y+threadIdx.y;
	int Col=blockIdx.x*blockDim.x+threadIdx.x;

	if((Row>>(m,n,k,d_a,d_b,d_c);

	//将结果传回到主机端
	cudaMemcpy(C, d_c, size*8, cudaMemcpyDeviceToHost);

	//输出结果
    for (int i=0;i<8;i++)
	{
		cout<

性能分析：

（1）低性能源于对globalmemory的访问

         a.Dynamic random access memory (DRAM)

         b.长的访问延迟（数百个时钟周期）

         c.有限的访问带宽

（2）对global memory存储交互拥塞导致少量线程可执行，使得SM闲置

3、通过shared memory提升优化GPU代码

使用shared memory带来两点优化：

（1）使用共享存储器减少了线程块中的线程必须访问的数据总量。

（2）使用共享存储器来实现存储空间的合并。（下篇文章展开介绍）

使用程序如下：

#include "cuda_runtime.h"
#include "device_launch_parameters.h"

#include 
using namespace std;
#define TILE_WIDTH 16  

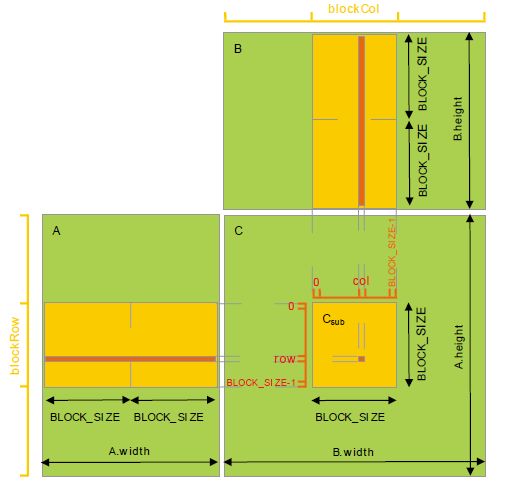
__global__ void MatrixMulKernle(int m, int n, int k, float *A,float  *B, float *C)
{
	 //申请共享内存，存在于每个block中
	__shared__ float ds_A[TILE_WIDTH][TILE_WIDTH]; 
	__shared__ float ds_B[TILE_WIDTH][TILE_WIDTH];

	//简化坐标记法,出现下面6个表示的地方就是并行的地方。
	int bx = blockIdx.x;		int by = blockIdx.y;
	int tx = threadIdx.x;		int ty = threadIdx.y;

	//确定结果矩阵中的行和列
	int Row = by * TILE_WIDTH + ty;
	int Col = bx * TILE_WIDTH + tx;

	//临时变量
	float Cvalue = 0;

	//循环读入A,B瓦片，计算结果矩阵，分阶段进行计算
	for (int t=0; t<(n-1)/TILE_WIDTH+1; ++t)
	{
		//将A,B矩阵瓦片化的结果放入shared memory中，每个线程加载相应于C元素的A/B矩阵元素
		if (Row < m && t * TILE_WIDTH + tx < n)		//越界处理，满足任意大小的矩阵相乘（可选）
			//ds_A[tx][ty] = A[t*TILE_WIDTH + tx][Row];
		    ds_A[tx][ty] = A[Row*n+t*TILE_WIDTH+tx];//以合并的方式加载瓦片
		else
			ds_A[tx][ty] = 0.0;

		if (t * TILE_WIDTH + ty < n && Col < k)
			//ds_B[tx][ty] = B[Col][t*TILE_WIDTH + ty];
            ds_B[tx][ty] = B[(t*TILE_WIDTH + ty)*k+Col];
		else
			ds_B[tx][ty] = 0.0;	

		//保证tile中所有的元素被加载
		__syncthreads();
		
		for (int i = 0; i < TILE_WIDTH; ++i)
            Cvalue += ds_A[i][ty] * ds_B[tx][i];//从shared memory中取值

		//确保所有线程完成计算后，进行下一个阶段的计算
		__syncthreads();

		if(Row < m && Col < k)
			C[Row*k+Col]=Cvalue;		
	}
}

int main()
{
	//这里将矩阵按照行优先转换成了一维的形式
	//实际中数组数量巨大，这里只是为了演示程序的过程
	float A[6] = { 11.4, 24, 33.5,   45, 55 ,32.4 }; //2×3的矩阵
	float B[12] = {12,43,22.4, 31.3,  12,324,23,12,  44.4,23.4,65.3,73};//3×4的矩阵
	float C[8] = { 0 }; //2×4的结果矩阵
	int m=2,n=3,k=4;

	//分配显存空间
	int size = sizeof(float);
	float *d_a;
	float *d_b;
	float *d_c;
	cudaMalloc((void**)&d_a,m*n*size);
	cudaMalloc((void**)&d_b,n*k*size);
	cudaMalloc((void**)&d_c,m*k*size);

	//把数据从Host传到Device
	cudaMemcpy(d_a, A, size*6, cudaMemcpyHostToDevice);
	cudaMemcpy(d_b, B, size*12, cudaMemcpyHostToDevice);
	cudaMemcpy(d_c, C, size*8, cudaMemcpyHostToDevice);

	//分配网格结构
	dim3 dimGrid((k-1)/TILE_WIDTH+1,(m-1)/TILE_WIDTH+1,1);	//向上取整
	dim3 dimBlock(TILE_WIDTH,TILE_WIDTH,1);

	//调用内核函数
	MatrixMulKernle<<>>(m,n,k,d_a,d_b,d_c);

	//将结果传回到主机端
	cudaMemcpy(C, d_c, size*8, cudaMemcpyDeviceToHost);

	//输出结果
	for (int i=0;i<8;i++)
	{
		cout<