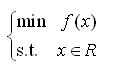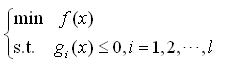压缩感知中的数学知识:凸优化
题目:压缩感知中的数学知识:凸优化
===================引言========================
压缩感知中会遇到凸优化的概念,就是什么把0范数转为1范数,变为凸优化问题……
要说明白凸优化的概念,得先知道凸集和凸函数的概念。
目录:
0、基础
1、凸集
2、凸函数
3、凸优化
参考文献:
1、唐焕文,秦学志.实用最优化方法(第三版)[M].大连理工大学出版社,2004.
本文主要以此书1.3节为主线。
2、机器学习&数据挖掘笔记_15(关于凸优化的一些简单概念),链接:http://www.cnblogs.com/tornadomeet/p/3300132.html
本文的第一幅插图采用此博文的插图。
3、凸优化(Convex optimization),链接:http://blog.sina.com.cn/s/blog_4b12446d01014iod.html
里面有几句话写的很好,正文里引用一下。
===================正文========================
0、基础
对于任意两点x和y,来自n维空间的Rn(n维实欧氏空间),则对于0<=μ<=1,关系μx+(1-μ)y表示x和y连线之间的所有点。
这是不是一个大家都知道的结论啊,但为什么我就是想不明白呢?我来证明一下吧,简化到一维的情况,即x和y就是两个实数。
假设y>x(即y-x>0),在一维情况下,只要证明x<=μx+(1-μ)y<=y就可以了。
证明:
x-[μx+(1-μ)y]=(1-μ)x-(1-μ)y=(1-[μx+(1-μ)y]<=0(因为1-μ>=0,x-y<0)
所以x<=μx+(1-μ)y
y-[μx+(1-μ)y]=μ(y-x)>=0
所以μx+(1-μ)y<=y
得证!
虽然这是一维上面证的,但在多维时可以将x和y分解啊,比如二维时可以分解成横坐标部和纵坐标部分,对于每一个坐标轴都是一维的,综合起来就得到了多维的结果。
所以心里要想着对于0<=μ<=1,关系μx+(1-μ)y表示x和y连线之间的所有点。
1、凸集
明白了上面的基础后,这个定义就简单了:
若某集合中的x和y两个点,若x和y连线之间的所有点(即0<=μ<=1,μx+(1-μ)y)仍属于这个集合,则称此集合为凸集。
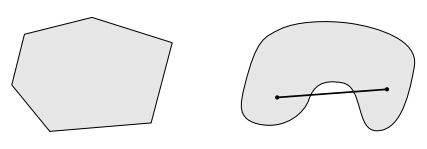
直观几何表示:
左边的是凸集,右边的不是凸集,因为右边的集合中任意两点x和y连线之间的所有点有时不属于这个集合(右图中的连线)。
2、凸函数
对于(x)是定义在某凸集(非空的,空集也被规定为凸集)上的函数,对于凸集中的任意两点x1和x2,若
f[μx1+(1-μ)x2]<=μf(x1)+(1-μ)f(x2)
则称函数f(x)为凸函数。
直观几何表示:
也就是说两点对应的函数值f(x1)和f(x2)的之间的连线(μf(x1)+(1-μ)f(x2))大于等于相应的(即同一个μ值)两点之间连线(μx1+(1-μ)x2)所对应的函数值f[μx1+(1-μ)x2]。
这其实应叫 下凸。
如果把上面不等式中的等号去掉,即
f[μx1+(1-μ)x2]<μf(x1)+(1-μ)f(x2) ,其中0<μ<1
则称f(x)为严格凸函数。
3、凸优化(凸规划)
若对于以下优化问题:
若目标函数f(x)是凸函数且可行集R是凸集,则称这样的问题为凸优化问题。
这个也可以换一种更一般的表达方式:对于以下优化问题
如果目标函数f(x)和共l个约束函数gi(x)都是凸函数,则称这样的问题为凸优化问题。
实际上,可以证明,约束函数gi(x)都是凸函数则它的可行集是凸集,具体证明如下(拍自参考文献1)
4、凸优化的特点
凸优说完了,到底凸优化有什么用呢?这里从三个参考文献分别摘几句话来说明:
1)如果一个实际的问题可以被表示成凸优化问题,那么我们就可以认为其能够得到很好的解决。【参考文献2】
2)还有的问题不是凸优化问题,但是凸优化问题同样可以在求解该问题中发挥重要的左右。比如松弛算法和拉格朗日松弛算法,将非凸的限制条件松弛为凸限制条件。【参考文献2】
3)对于凸优化问题来说,局部最优解就是全局最优解。【参考文献3】
4)若f(x)在非空可行集R上是严格凸函数,则问题(3-8)的全局极小点是唯一的。【参考文献1】
也就是说如果把一个非凸优化问题转化为凸优化问题(松弛算法),则若求得一个局部最优解即为得到了全局最优解(若目标函数在可行集上是严格凸函数,则此解还是唯一的),并且凸优化问题能够比较好的得解决,因此在看压缩感知的文献时经常会看到如何如之何修改一下约束条件使之变为一个凸优化问题。
凸优化有很多专著,对于某些专业好像还是一门专业课,不得不感叹自己的眼界之小……
===================感慨========================
近来看东西看的发现自己是个数学小白,说啥啥不懂,喀,还不能说不懂,应该说是说啥啥都没听过……
路漫漫其修远兮,吾将上下左右而求索……