浅谈字符串匹配算法—BF算法及KMP算法
字符串匹配,在实际编程中经常遇到。其相应的算法有很多,本文就BF算法和KMP算法,谈一下自己的理解。并结合平时编程,修改了一下,使其更符合我们的使用习惯。(注:标准BF算法和KMP算法,为研究方便,其字符数组[0]存放的都是字符串的长度。本文讲解中,并没有保存字符串长度。后面给出的示例代码中,字符数组中是否保存有字符串长度,都给出了相应的算法代码。)
一、BF算法(Brute Force):
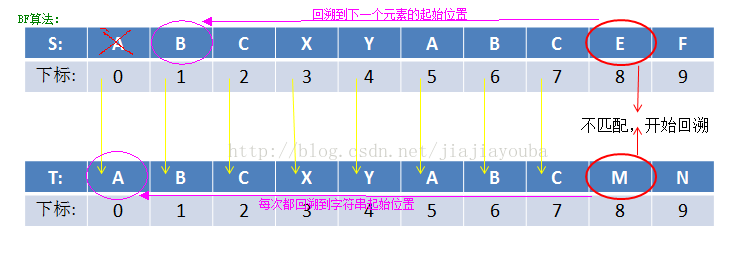
BF算法核心思想是:首先S[1]和T[1]比较,若相等,则再比较S[2]和T[2],一直到T[M]为止;若S[1]和T[1]不等,则T向右移动一个字符的位置,再依次进行比较。如果存在k,1≤k≤N,且S[k+1…k+M]=T[1…M],则匹配成功;否则失败。该算法最坏情况下要进行M*(N-M+1)次比较,时间复杂度为O(M*N)。下面结合图片,解释一下:
S代表源字符串,T代表我们要查找的字符串。BF算法可以表述如下:依次遍历字符串S,看是否字符串S中含有字符串T。因此,我们依次比较S[0] 和T[0]、S[1] 和T[1]、S[2] 和T[2]……S[n]和T[n] ,从图中我们可知,S[0]-S[7]和T[0]-T[7]依次相等。当匹配到S[8]和T[8]时,两个字符不等。根据定义,此时S和T都要回溯,T向右移动一个字符的位置,即S回溯到S[1]的位置,T回溯到T[0]的位置,再重新开始比较。此时,S[1]和T[0]、S[2]和T[1]……如果再次发现不匹配字符,则再次回溯,即S回溯到S[2]的位置,T回到T[0]的位置。循环往复,直到到达S或者T字符串的结尾。如果是到达S串的结尾,则表示匹配失败,如果是到达T串的结尾,则表示匹配成功。
BF算法优点:思想简单,直接,无需对字符串S和T进行预处理。缺点:每次字符不匹配时,都要回溯到开始位置,时间开销大。
下面是BF算法的代码实现:bf.c
#include
#include
#include
int index_bf(char *s,char *t,int pos);
int index_bf_self(char *s,char *t,int index);
/*
BF算法 示例
*/
int main()
{
char s[]="6he3wor"; //标准BF算法中,s[0]和t[0]存放的为字符串长度。
char t[]="3wor";
int m=index_bf(s,t,2); //标准BF算法
printf("index_bf:%d\n",m);
m=index_bf_self(s,t,2); //修改版BF算法,s和t中,不必再存放字符串长度。
printf("index_bf_self:%d\n",m);
exit(0);
}
/*
字符串S和T中,s[0],t[0]存放必须为字符串长度
例:s[]="7hi baby!" T[]="4baby" index_bf(s,t,1);
pos:在S中要从下标pos处开始查找T
(说明:标准BF算法中,为研究方便,s[0],t[0]中存放的为各自字符串长度。)
*/
int index_bf(char *s,char *t,int pos)
{
int i,j;
if(pos>=1 && pos <=s[0]-'0')
{
i=pos;
j=1;
while(i<=s[0]-'0'&&j<=t[0]-'0')
{
if(s[i]==t[j])
{
i++;
j++;
}
else
{
j=1;
i=i-j+2;
}
if(j>t[0]-'0')
{
return i-t[0]+'0';
}
}
return -1;
}
else
{
return -1;
}
}
/*
修改版,字符串s和t中,不必再包含字符串长度。
例:s[]="hi baby" t[]="baby" index_bf_self(s,t,0);
index:在s中,从几号下标开始查找
*/
int index_bf_self(char *s,char *t,int index)
{
int i=index,j=0;
while(s[i]!='\0')
{
while(*(t+j)!='\0' && *(s+i+j)!='\0')
{
if(*(t+j)!=*(s+i+j))
break;
j++;
}
if(*(t+j)=='\0')
{
return i;
}
i++;
j=0;
}
return -1;
} 测试结果:
二、KMP算法:
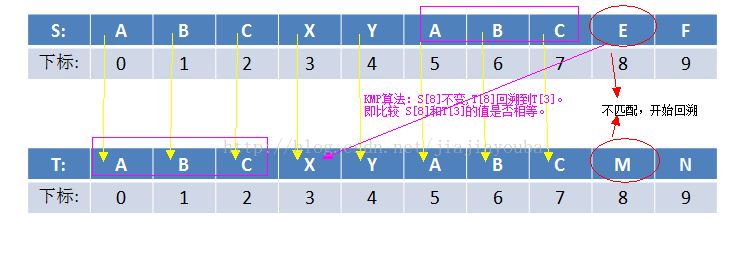
由BF算法例图中可知,当S[8]和T[8]不匹配时,S和T都需要回溯,时间复杂度高。因此,出现了KMP算法。先看下图:
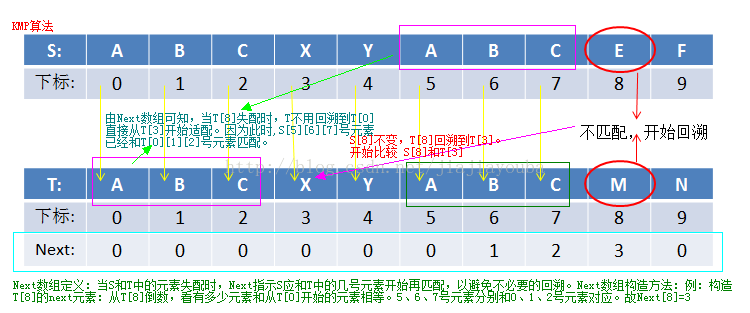
从图中,我们可以很容易的发现,S不必回溯到S[1]的位置,T也不必回溯到T[0]的位置,因为前面的字符,S和T中都是相等的。如果S不回溯的话,那T该怎么办呢?我们也可以很容易的发现,S中5、6、7号字符和T中0、1、2号字符是相等的。故T直接回溯到T[3]的位置即可。此时我们就省去了很多不必要的回溯和比较。那么这些都是我们从图中直观得出的结论,如果换做其他字符,我们又如何知道T该回溯到几号字符呢?
先看看KMP算法的思想:假设在模式匹配的进程中,执行T[i]和W[j]的匹配检查。若T[i]=W[j],则继续检查T[i+1]和W[j+1]是否匹配。若T[i]<>W[j],则分成两种情况:若j=1,则模式串右移一位,检查T[i+1]和W[1]是否匹配;若1 图中,首先构造 Next 数组,构造过程见图解(这里讲解的简单了些,本文重点是理清KMP算法思路,故没有赘述,想细究的同学,自己谷歌一下吧)。构造完毕后,当S[8]和T[8]失配时,我们从next 数组可知,T应回溯到T[3]的位置,重新开始比较。样子有点像下面这样: 如果S[8]和T[3]再次失配,则继续回溯,即比较S[8]和T[0]。如果再次失配,T已无回溯元素可言,此时,S向后移动,即开始比较S[9]和T[0]……结束条件就是:到达字符串S或者T的结尾。若是S结尾,则返回-1.若是T结尾,则匹配成功。返回S中T串开始时的下标即可。 下面给出个小例子,仅供大家练习使用: 下面给出KMP算法标准代码(即数组首元素保存的是字符串长度):kmp.c 修改版KMP算法:(字符数组首元素不再保存字符串长度,更符合实际应用) kmp2.c
示例测试结果:
#include #include
示例测试结果: