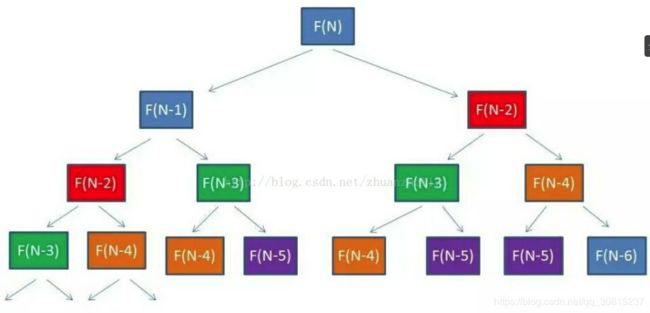
动态规划问题

 

     动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

     假设问题是由交叠的子问题所构成，我们就能够用动态规划技术来解决它。一般来说，这种子问题出自对给定问题求解的递推关系中，这个递推关系包括了同样问题的更小子问题的解。动态规划法建议，与其对交叠子问题一次重新的求解，不如把每一个较小子问题仅仅求解一次并把结果记录在表中（动态规划也是空间换时间的）。这样就能够从表中得到原始问题的解。

0-1 背包问题：

    给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi 。问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

     解决办法：声明一个 大小为  m[n][c] 的二维数组，m[ i ][ j ] 表示 在面对第 i 件物品，且背包容量为  j 时所能获得的最大价值 ，那么我们可以很容易分析得出 m[i][j] 的计算方法，

（1）. j < w[i] 的情况，这时候背包容量不足以放下第 i 件物品，只能选择不拿：  m[ i ][ j ] = m[ i-1 ][ j ]

（2）. j>=w[i] 的情况，这时背包容量可以放下第 i 件物品，我们就要考虑拿这件物品是否能获取更大的价值。

      如果拿取，m[ i ][ j ]=m[ i-1 ][ j-w[ i ] ] + v[ i ]。 这里的m[ i-1 ][ j-w[ i ] ]指的就是考虑了i-1件物品，背包容量为j-w[i]时的最大价值，也是相当于为第i件物品腾出了w[i]的空间。

    如果不拿，m[ i ][ j ] = m[ i-1 ][ j ] , 比较这两种情况那种价值最大。状态方程：

if(j>=w[i])
    m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
    m[i][j]=m[i-1][j];

1. def bag01(value,weight,n,c):

2. dp=[[0 for i in range(c+1)] for j in range(n+1)]

3. for i in range(1,n+1):

4. for j in range(1,c+1):

5. if j>weight[i]:

6. m[i][j]=np.maxinum(m[i-1][j-weight[i]]+value[i],m[i-1][j])

7. else:

8. m[i][j]=m[i-1][j]

9. return dp[n][c]

from：https://blog.csdn.net/code17710597026/article/details/52107827

1、走方格问题

      有一个矩阵map，它每个格子有一个权值。从左上角的格子开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，返回所有的路径中最小的路径和。给定一个矩阵map及它的行数n和列数m，请返回最小路径和。保证行列数均小于等于100.

1. #递归法

2. def getminway(m,n,map):

3. if m==1:

4. return sum(map[0,0:m-1])

5. if n==1:

6. return sum(map[0:m-1,0])

7. return min(getminway(m-1,n,map),getminway(m,n-1,map))+1

8.  
9.  

10. #动态规划

11. def getminway(m,n,map):

12. dp=[[0 for i in range(n) for j in range(m)]]

13. dp[0][0]=map[0,0]

14. for i in range(m-1):

15. dp[i+1][0]=dp[i][0]+map[i+1,0]

16. for j in range(n-1):

17. dp[0][j+1]=dp[0][j]+map[0,j+1]

18. for i in range(1,m):

19. for j in range(1,n):

20. dp[i][j]=min(dp[i-1][j]+map[i,j],dp[i][j-1]+map[i,j])

21. return dp[m-1][n-1]

    有一个M乘N的网格，一个机器人只能走格点且只能向右或向下走，要从左上角走到右下角。请设计一个算法，计算机器人有多少种走法。

1. #递归法

2. def countway(m,n):

3. if m==1 or n==1:

4. return 1

5. return countway(m-1,n)+countway(m,n-1)

6.  

7. #动态规划

8. def countway(m,n):

9. dp=[[0 for i in range(n)]for j in range(m)]

10. for i in range(m):

11. dp[i][0]=1

12. for i in range(n):

13. dp[0][i]=1

14. for i in range(m):

15. for j in range(n):

16. dp[i][j]=dp[i-1][j]+dp[i][j-1]

17. return dp[m - 1][n - 1]

from :https://blog.csdn.net/guotong1988/article/details/99578056

2、走台阶问题

    有n级台阶，一个人每次上一级或者两级，问有多少种走完n级台阶的方法。为了防止溢出，请将结果Mod 1000000007
给定一个正整数int n，请返回一个数，代表上楼的方式数。保证n小于等于100000。

    解析：这是一个非常经典的为题，设f(n)为上n级台阶的方法，要上到n级台阶的最后一步有两种方式：从n-1级台阶走一步；从n-1级台阶走两步，于是就有了这个公式f(n) = f(n-1)+f(n-2);

思路：一种是递归，一种是动态规划

递归的时间复杂度为2的n次方。

1. def countWays(n):

2. if n<=2:

3. return n

4. return countWays(n-1)+countWays(n-2)

    这是一棵二叉树，如图所示，这里同样颜色的表示重复计算的节点，而且多数都不止重复计算了一次。我们可以对此进行优化，使用哈希表存储已经计算的节点，不再重复计算。

动态规划：

1. def countWays(n):

2. if n<=2:

3. return n

4. a=1

5. b=2

6. for i in range(3,n+1):

7. temp=a+b

8. a=b

9. b=temp

10. return temp

from：https://blog.csdn.net/zhuanzhe117/article/details/72846939

3、最长公共序列数

  给定两个字符串A和B，返回两个字符串的最长公共子序列的长度。例如，A="1A2C3D4B56”，B="B1D23CA45B6A”，

”123456"或者"12C4B6"都是最长公共子序列。给定两个字符串A和B，同时给定两个串的长度n和m，请返回最长公共子序列的长度。保证两串长度均小于等于300。
测试样例："1A2C3D4B56",10,"B1D23CA45B6A",12
返回：6

第一种方法：

1、把两个字符串分别以行和列组成一个二维矩阵。

2、比较二维矩阵中每个点对应行列字符中否相等，相等的话值设置为1，否则设置为0。

3、通过查找出值为1的最长对角线就能找到最长公共子串。

     针对于上面的两个字符串我们可以得到的二维矩阵，为了进一步优化算法的效率，我们可以再计算某个二维矩阵的值的时候顺便计算出来当前最长的公共子串的长度，即某个二维矩阵元素的值由record[i][j]=1演变为record[i][j]=1 +record[i-1][j-1]，这样就避免了后续查找对角线长度的操作了。修改后的二维矩阵如下：

                          

1. def find_lcsubstr(s1, s2):

2. m=[[0 for i in range(len(s2+1))] for j in range(len(s1+1))]

3. maxlen=0

4. p=0

5. for i in range(len(s1)):

6. for j in range(len(s2)):

7. if s1[i]==s2[j]:

8. m[i+1][j+1]==m[i][j]+1

9. if m[i+1][j+1]>maxlen:

10. maxlen=m[i+1][j+1]

11. p=i+1

12. return s1[p-maxlen:p],maxlen

 

动态规划：

  解析：设dp[n][m] ，为a的前n个字符与b的前m个字符的公共序列长度，则转移方程：

dp[i,j] = dp[i-1][j-1]+1                        i>0,j>0, a[i] = b[j]       

dp[i,j] = max(dp[i-1][j],dp[i][j-1])        i>0,j>0, a[i] != b[j]

1. def findLCS(a,b,m,n):

2. dp=[[0 for i in range(n)] for j in range(m)]

3. for i in range(m):

4. if a[i]==b[0]:

5. dp[i][0]=1

6. for j in range(i+1,m):

7. dp[i][0]=1

8. for i in range(n):

9. if b[i]==a[0]:

10. dp[0][i]=1

11. for j in range(i+1,n):

12. dp[0][i] = 1

13. for i in range(1,m):

14. for j in range(1,n):

15. if a[i]==b[j]:

16. dp[i][j]=dp[i-1][j-1]+1

17. else:

18. dp[i][j]=np.maxinum(dp[i-1][j],dp[i][j-1])

19. return dp[m-1][n-1]

4、最大连续子序列之和

     给定K个整数的序列{ N1, N2, …, NK }，其任意连续子序列可表示为{ Ni, Ni+1, …, Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序中元素和最大的一个， 例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和为20。

下面介绍动态规划的做法，复杂度为 O(n)。

　　步骤 1：令状态 dp[i] 表示以 A[i] 作为末尾的连续序列的最大和（这里是说 A[i] 必须作为连续序列的末尾）。

　　步骤 2：做如下考虑：因为 dp[i] 要求是必须以 A[i] 结尾的连续序列，那么只有两种情况：

1.  这个最大和的连续序列只有一个元素，即以 A[i] 开始，以 A[i] 结尾。
2.  这个最大和的连续序列有多个元素，即从前面某处 A[p] 开始 (p

对第一种情况，最大和就是 A[i] 本身。对第二种情况，最大和是 dp[i-1]+A[i]。于是得到状态转移方程：

　　　　　　　　dp[i] = max{A[i], dp[i-1]+A[i]}

　　这个式子只和 i 与 i 之前的元素有关，且边界为 dp[0] = A[0]，由此从小到大枚举 i，即可得到整个 dp 数组。接着输出 dp[0]，dp[1]，...，dp[n-1] 中的最大子即为最大连续子序列的和。

1. def getmax(A):

2. dp=[0]*len(A)

3. dp[0]=A[0]

4. for i in range(1,len(A)):

5. dp[i]=np.maximun(dp[i-1]+A[i],A[i])

6. return max(dp[i])

from:https://blog.csdn.net/qq_37763204/article/details/79394397

5、最长递增子序列(LIS)

给定一个序列 An = a1 ,a2 ,  … , an ，找出最长的子序列使得对所有 i < j ，ai < aj 。

转移方程：b[k]=max(max(b[j]|a[j]

1. def getLIS(a):

2. b=[0]*len(a)

3. b[0]=1

4. for i in range(1,len(a)):

5. b[i]=1

6. for j in range(i):

7. if a[i]>a[j] and b[i]<=b[j]: #

8. b[i]=b[j]+1 #更新

9. return max(b)