图像检索与降维(一):VLAD
论文地址:https://lear.inrialpes.fr/pubs/2010/JDSP10/jegou_compactimagerepresentation.pdf
在大规模图像集中搜索需要解决三个问题:1.搜索的准确率 2.搜索算法效率 3.图像特征所占内存。而后两项是相关的,因为搜索效率可以近似与访问内存次数相等。在第一个问题上,bag-of-features image representation (BOF) 与VLAD最为相似,BOF使用的近似最近邻搜索来获得BOF向量。然而,使用较低维度的BOF向量来进行图像搜索,只能得到比较低的搜索准确率,并且这种较低维度的BOF向量依然还需要上百比特的大小。第二个问题,搜索算法的效率问题,可以由min-Hash解决,但是这些方法仍然在每张图片上需要花费大量的内存。VLAD方法可以获得更高的准确率,重要的是,只需要20比特大小的图像表示,这通过优化1. 图像表示(例如:如何聚集局部图像特征为一个向量表示) 2.这些向量的降维 3.索引算法。这三个步骤是十分相关的,通过一个高维向量表示一张图像经常可以比一个低维向量得到更加详细的搜索结果。但是,高维向量的索引效率要低很多。相反,一个低维向量更容易被索引,但是它的判别能力就要略低,并且可能对识别物体或者场景来说,其信息是不够的。
VLAD的第一个优点在于提出一种图像表示方法,在拥有合理的向量维度下,具有很好的搜索准确率。第二个优点在于联合优化降维和索引效率。
图像向量表示(VLAD)
VLAD通过聚合特征空间的局部信息来产生一个图像表示向量,这个过程可以看做是Fisher kernel的简化版。和BOF类似,首先先通过k-means学习一个大小为k的码书 C = c 1 , . . . c k \mathcal{C}={c_1,...c_k} C=c1,...ck。每一个局部点x与其最近的聚点 c i = N N ( x ) c_i = NN(x) ci=NN(x)相联系,VLAD描述向量的关键是累加,对于每个 c i c_i ci,累加 x − c i x-c_i x−ci:
v i , j = ∑ x j − c i , j v_{i,j} = \sum x_j - c_{i,j} vi,j=∑xj−ci,j
其中 x j , c i , j x_j,c_{i,j} xj,ci,j分别表示第j个x局部点和其对应最近的聚点。假设x的维度为d,如此就可以得到维度为D=k*d大小的向量v。随后再将v进行L2标准化: v : = v / ∣ ∣ v ∣ ∣ 2 v:=v/||v||_2 v:=v/∣∣v∣∣2。
下图是当k=5时求VLAD的示例:
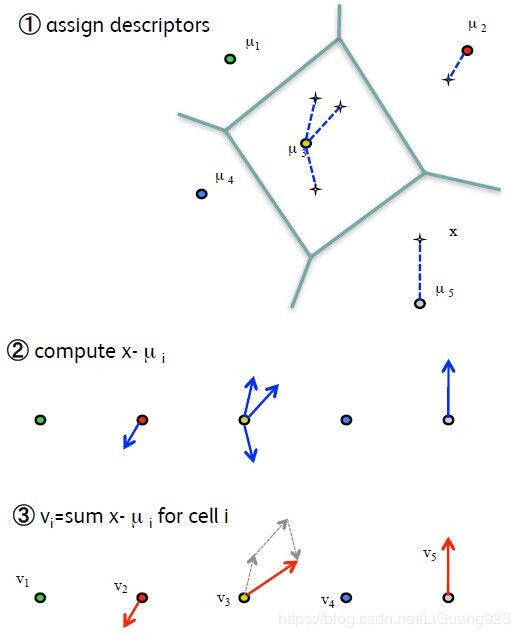
在VLAD向量中,表示特征是相对稀疏的(少部分值拥有较大的能量)并且非常具有结构性的。大多数具有较高的表征量的信息都位于同一个聚类中,并且SIFT的几何结构是比较直观的,后面可能使用PAC来捕获这种结构信息,对于充分相似的图像,其表示向量的接近程度一般来说是很明显的。
以上就是VLAD向量的获取过程,至此就可以使用VLAD向量进行检索了,而在实际情况中,聚点数量其实是比较多的,这样在求解VLAD(尤其是每个点对应的最近聚点时)的效率其实比较低的,另外,k*d大小的VLAD虽然比之前的方法要小,但是在大图像库中的索引效率依然还不够,以下则是作者提出的一些优化方法,即在索引效率和降维上进行优化。
向量编码
对于D维的输入向量,我们想要产生一个B字节的编码用于表示图像以至于在搜索过程中能够更有效率,VLAD将通过两个步骤处理这个问题,通过联合优化:1.降维 2.量化索引结果向量。这个过程通过asymmetric distance computation (ADC)实现。
ADC
假设k为聚点个数,为了获得一个较好的近似向量,k一般为 2 64 2^{64} 264,64个比特大小。而对于如此大的一个k,要学习一个k-means码书是不容易的。文中的解决方法是使用一个积量化,向量x首先被分为m个子向量 x 1 , . . . x m x^1,...x^m x1,...xm,每一个长度为D/m。这个积量化被定义为以下函数:
q ( x ) = ( q 1 ( x 1 ) , . . . , q m ( x m ) ) q(x) = (q_1(x^1),...,q_m(x^m)) q(x)=(q1(x1),...,qm(xm))
每个单独的量化器 q j ( ) q_j() qj()通过kmeans学习得到 k s k_s ks个再生值,为了限制其复杂度 O ( m ∗ k s ) \mathcal{O}(m*k_s) O(m∗ks), k s k_s ks是一个较小的值,比如256.然后通过分解计算求得x的最近聚点:
∣ ∣ x − q ( y i ) ∣ ∣ 2 = ∑ ∣ ∣ x j − q j ( y i j ) ∣ ∣ 2 ||x-q(y_i)||^2 = \sum||x^j - q_j(y_i^j)||^2 ∣∣x−q(yi)∣∣2=∑∣∣xj−qj(yij)∣∣2
其中 y i j y_i^j yij是聚点 y i y_i yi的第j个子向量。而通过这样获得码书的复杂度就由 O ( D ∗ n ) \mathcal{O}(D*n) O(D∗n)变为了 O ( D ∗ k s ) \mathcal{O}(D*k_s) O(D∗ks),而 k s < < n k_s<<n ks<<n。
另外,作者指出将 y i y_i yi通过量化器q分解其实是存在误差的:
y i = q ( y i ) + ε q ( y i ) y_i = q(y_i) + \varepsilon_q(y_i) yi=q(yi)+εq(yi)
ε q ( y i ) \varepsilon_q(y_i) εq(yi)为产生的误差。
降维
降维是最近邻搜索的一个重要步骤,因为它影响了随后的索引方法。对于ADC方法,通过一个简单的近似误差测量用于在降维和索引机制之间进行权衡。假设向量的均值为一个空向量(之前将向量进行了标准化),PCA是一种标准的降维方法:D‘个最具能量的特征值所对应的特征向量组成的矩阵M,将向量x映射为x’ = Mx。这种降维也可以被描述为是在原始空间中的一种映射。在这种情况下,x被近似为:
x p = x − ε p ( x ) x_p = x -\varepsilon_p(x) xp=x−εp(x)
ε p ( x ) \varepsilon_p(x) εp(x)表示为映射过程中产生的误差,然后向量x’随后再通过ADC方法被编码为q(x’):
q ( x p ) = x − ε p ( x ) − ε q ( x ) q(x_p) = x - \varepsilon_p(x) - \varepsilon_q(x) q(xp)=x−εp(x)−εq(x)
其中又产生了误差 ε q ( x ) \varepsilon_q(x) εq(x),这就存在了一个需要微调的地方,即PAC降维后的维度D’如果过大,那么映射误差 ε p ( x ) \varepsilon_p(x) εp(x)将较小,但是量化误差 ε q ( x ) \varepsilon_q(x) εq(x)则将变大。相反,保持较小的D’将导致一个较高的映射误差和较低的量化误差。
这里通过在PCA后执行一个正交转换来解决该问题,我们想要找到这样的一个正交矩阵Q,以至于转换后的向量X’’ = QX’ = QMX具有相同的方差。这可以通过最小化ADC方法中的量化误差来获得矩阵Q’:
Q ′ = a r g m i n ( E x [ ∣ ∣ ε q ( Q M X ) ∣ ∣ 2 ] ) Q' = argmin (E_x[||\varepsilon_q(QMX)||^2]) Q′=argmin(Ex[∣∣εq(QMX)∣∣2])
然而,该优化问题并不好完成,因为该目标函数需要在每一次迭代中计算ADC结构的积量化器q()。找到满足简化平衡目标的矩阵Q可以通过Householder矩阵的形式来完成:
Q = I − 2 v v T Q = I-2vv^T Q=I−2vvT
其中的v为v的前D‘成分。
联合优化降维和索引
VLAD向量和x的欧式距离平方等于误差 ∣ ∣ ε p ( x ) ∣ ∣ 2 ||\varepsilon_p(x)||^2 ∣∣εp(x)∣∣2和 ∣ ∣ ε q ( x ) ∣ ∣ 2 ||\varepsilon_q(x)||^2 ∣∣εq(x)∣∣2之和,ADC方法减小 ε q ( x ) \varepsilon_q(x) εq(x)可以加快索引效率,在PCA中减少 ε q ( x ) \varepsilon_q(x) εq(x)可以减少信息损失,由上可知,这两个误差依赖于D’(PCA中选择的维数),所以,通过 e ( D ′ ) e(D') e(D′)用于在向量集 L \mathcal{L} L上测量误差:
e ( D ′ ) = e p ( D ′ ) + e q ( D ′ ) = 1 / c a r d ( L ) ∑ x ∈ L ∣ ∣ ε p ( x ) ∣ ∣ 2 + ∣ ∣ ε q ( x ) ∣ ∣ 2 e(D') = e_p(D') + e_q(D') = 1/card(\mathcal{L}) \sum_{x \in \mathcal{L} }||\varepsilon_p(x)||^2 + ||\varepsilon_q(x)||^2 e(D′)=ep(D′)+eq(D′)=1/card(L)x∈L∑∣∣εp(x)∣∣2+∣∣εq(x)∣∣2
通过最小化该目标函数用于获得最佳D’。
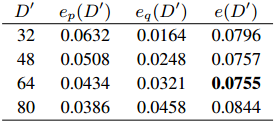
以上是作者关于D’选择的一组实验结果,当D‘为64时,可以使得误差最小。
参考
https://blog.csdn.net/breeze5428/article/details/36441179