Java数据结构之234树
N叉树简介
每个节点只有一个数据项,并且每个节点最多只有两个子节点的树称为二叉树。如果每个节点可以存多个(大于等于3)数据项,并且每个节点可以拥有多个(大于等于3)子节点的树称为N(大于等于3)叉树。N叉树相对于二叉树而言,存储相等数量的数据,N叉树因为同一层存放的数据变多,相应树的高度就变小,查询也就更快。
234树简介
234树的特点
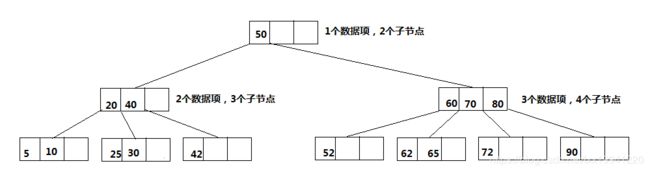
234树是N叉树的一种,其中数字2、3、4可以认为是节点的子节点数量,234树主要有以下特点:
- 一个节点最多可以存储3个数据项。
- 一个节点(非叶节点)最多拥有4个子节点。
- 数据项个数与子节点数量关系为:子节点数量 = 数据项个数 + 1。
- 一个节点(非叶节点)存有1个数据项时,拥有2个子节点。
- 一个节点(非叶节点)存有2个数据项时,拥有3个子节点。
- 一个节点(非叶节点)存有3个数据项时,拥有4个子节点。
- 234树中不存在空节点(没有数据项的节点),这个可以从后面的分裂看出来。
数据存放规则
假如一个节点中有三个数据项(从左往右为:D1,D2,D3),那么其4个子节点(从左往右为:C1,C2,C3,C4),有如下大小关系:C1节点数据项及其子节点数据项 < D1 < C2节点数据项及其子节点数据项 < D2 < C3节点数据项及其子节点数据项 < D3 < C4节点数据项及其子节点数据项 。
插入数据
234树插入数据,数据总是插入在叶子节点,跟二叉树一样会向下查找合适的叶子节点,再次过程中核能会发生一系列节点变换(节点分裂),找到叶子节点后,然后根据节点数据项排列顺序(左侧数据项 < 中间数据项 < 右侧数据项)将数据放入节点数据项中。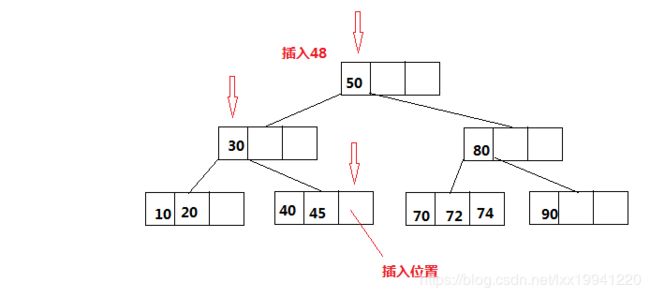
节点分裂
插入数据时,在向下寻找过程中如果遇到了数据项已经满了的节点(拥有三个数据项),将会对改节点进行分裂,假如节点三个数据项从左往右为D1、D2、D3,四个子节点从左往右分别为C1、C2、C3、C4,分裂规则是:
- 将D2数据项上移,作为父节点的数据项(父节点最多只有两个数据项),创建分裂节点的兄弟节点,将D1数据项作为兄弟节点的数据项,C1,C2作为兄弟节点的子节点,分裂完毕。
- 如果D2节点上移过程中,没有父节点,即分裂节点为根节点,则新建根节点,然后D2作为根节点的数据项。

代码实现
节点类
package com.lxx.tree;
/**
* 234树节点类
* 这里为了简便实现,节点类的数据项为Integer数据
* @author lxx
*/
public class Node234 {
// 节点子节点数量最多为4
private static final int CHILD_NODE_COUNT = 4;
// 节点数据项个数
private int dataItemCount;
// 父节点
private Node234 parent;
// 子节点
private Node234[] children = new Node234 [CHILD_NODE_COUNT];
// 节点数据项
private Integer[] dataItems = new Integer [CHILD_NODE_COUNT -1];
// 构造方法
public Node234() {
this.dataItemCount = 0;
}
// 判断当前节点是否已满
public boolean isFull() {
return (dataItemCount == CHILD_NODE_COUNT -1);
}
// 获取父节点
public Node234 getParent() {
return parent;
}
// 获取指定位置的子节点
public Node234 getChild(int childIndex) {
return children[childIndex];
}
// 判断节点是否为叶子节点
public boolean isLeafNode() {
return children[0] == null;
}
// 获取节点的数据项个数
public int getDataItemCount() {
return dataItemCount;
}
// 获取指定位置的数据项
public int getDataItem(int dataItemIndex) {
return dataItems[dataItemIndex];
}
// 连接子节点
public void connectChild(int childIndex, Node234 child) {
if(child != null) {
children[childIndex] = child;
child.parent = this;
}
}
// 去掉子节点
public Node234 removeNode(int childIndex) {
Node234 removeNode = children[childIndex];
children[childIndex] = null;
return removeNode;
}
// 查找具体数据项在数据项数组中的索引位置
public int findDataItemIndex(Integer dataItem) {
for(int i=0; i< CHILD_NODE_COUNT-1; i++) {
if(dataItems[i] == null) {
break;
}else if(dataItems[i].equals(dataItem)) {
return i;
}
}
return -1;
}
//插入数据项
public int insertItem(Integer newDataItem) {
dataItemCount ++;
for(int i=CHILD_NODE_COUNT-2; i>=0; i--) {
if(dataItems[i] == null) {
continue;
}
if(newDataItem < dataItems[i]) {
dataItems[i+1] = dataItems[i];
}else {
dataItems[i+1] = newDataItem;
return i+1;
}
}
dataItems[0] = newDataItem;
return 0;
}
//删除大数据项
public Integer removeDataItem() {
Integer removeDataItem = dataItems[dataItemCount - 1];
dataItems[dataItemCount - 1] = null;
dataItemCount --;
return removeDataItem;
}
// 打印节点
public void displayNode() {
for (int i=0; i234树实现
package com.lxx.tree;
/**
* 234树实现类
*
* @author lxx
*/
public class Tree234 {
// 根节点
private Node234 root = new Node234();
// 利用当前节点和数据项的值,查找写一个子节点
public Node234 getNextChild(Node234 currentNode, Integer nowDataItem) {
// 获取当前节点的数据项个数
int dataItemCount = currentNode.getDataItemCount();
// 遍历比较
for (int j = 0; j < dataItemCount; j++) {
if (nowDataItem < currentNode.getDataItem(j)) {
// 数据项比当前节点数据项比较,小于的话,返回左侧的子节点
return currentNode.getChild(j);
}
}
// 传入数据项值比当前节点数据项都大,返回最右侧子节点
return currentNode.getChild(dataItemCount - 1);
}
// 判断否数据项是否存在
public boolean isExist(Integer dataItem) {
Node234 currentNode = root;
while (true) {
if (currentNode.findDataItemIndex(dataItem) != -1)
// 在当前节点找到该数据项,返回索引
return true;
else if (currentNode.isLeafNode())
return false;
else
currentNode = getNextChild(currentNode, dataItem);
}
}
// 插入一个数据项
public void add(Integer dataItem) {
Node234 currentNode = root;
while (true) {
if (currentNode.isFull()) {
// 当前节点满了,分裂当前节点
split(currentNode);
currentNode = currentNode.getParent();
currentNode = getNextChild(currentNode, dataItem);
} else if (currentNode.isLeafNode())
break;
else
currentNode = getNextChild(currentNode, dataItem);
}
currentNode.insertItem(dataItem);
}
// 分裂节点
public void split(Node234 currentNode) {
// 定义从左到右 第二个数据项 和 第三个数据项
Integer item, rightItem;
// 定义父节点 ,以及最右侧两个子节点
Node234 parent, child3, child4;
int itemIndex;
// 记录当前节点第三个数据项,并删除
rightItem = currentNode.removeDataItem();
// 记录当前节点第二个数据项,并删除
item = currentNode.removeDataItem();
// 记录当前节点第三个子节点,并删除
child3 = currentNode.removeNode(2);
// 记录当前节点第四个子节点,并删除
child4 = currentNode.removeNode(3);
// 创建分裂节点兄弟节点
Node234 brotherNode = new Node234();
// 分裂节点的最大数据项作为兄弟节点的数据下个
brotherNode.insertItem(rightItem);
// 分裂节点的第三个和第四个子节点作为兄弟节点的子节点
brotherNode.connectChild(0, child3);
brotherNode.connectChild(1, child4);
// 开始分裂
if (currentNode == root) {
// 根节点分裂情况,创建新的根节点,原根节点作为新根节点的子节点,并记录分裂节点的父节点
root = new Node234();
parent = root;
root.connectChild(0, currentNode);
} else {
// 记录分裂节点的父节点
parent = currentNode.getParent();
}
// 将要分裂节点的的中间数据项插入到父节点中 并且获取到插入的索引
itemIndex = parent.insertItem(item);
// 获取父节点中数据项的个数
int dataItemCount = parent.getDataItemCount();
// 循环根据
for (int j = dataItemCount - 1; j > itemIndex; j--) { //
Node234 temp = parent.removeNode(j); // 父节点和要拆分的接待你断开连接
parent.connectChild(j + 1, temp); // 父节点和要拆分的原节点重新连接 位置为原要拆分节点的中间的数据项在父节点中位置的左边
}
parent.connectChild(itemIndex + 1, brotherNode); // 然后在原要拆分节点新的位置的右边插入新的右边节点
}
// 打印一整棵树
public void displayTree() {
recDisplayTree(root, 0, 0);
}
// 打印树 传入要从那个节开始打 从那层开始的 哪个节点开始的 前序遍历
private void recDisplayTree(Node234 thisNode, int level, int childNumber) {
System.out.print("level=" + level + " child=" + childNumber + " "); // 先打印当前节点的状况
thisNode.displayNode();
int dataItemCount = thisNode.getDataItemCount();
for (int j = 0; j < dataItemCount + 1; j++) { // 遍历每一个子节点并打印 递归
Node234 nextNode = thisNode.getChild(j);
if (nextNode != null) // 如果
recDisplayTree(nextNode, level + 1, j); // 向下层递归
else
return; // 递归结束
}
}
}

