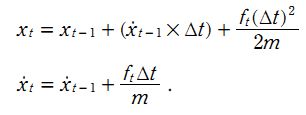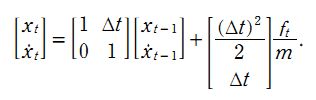卡尔曼滤波 - - 附C++程序

        写博客记录下做过的工作，毕竟好记性不如烂笔头。

        卡尔曼滤波算法的博客很多，白巧克力亦唯心http://blog.csdn.net/heyijia0327的阐述应该是较为通俗易懂的，他的理论部分是参考Greg Welch & Gary Bishop. << An Introduction to the Kalman Filter >>，实例小车部分类似文章Ramsey Faragher. << Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation >>，网上都可以找到。

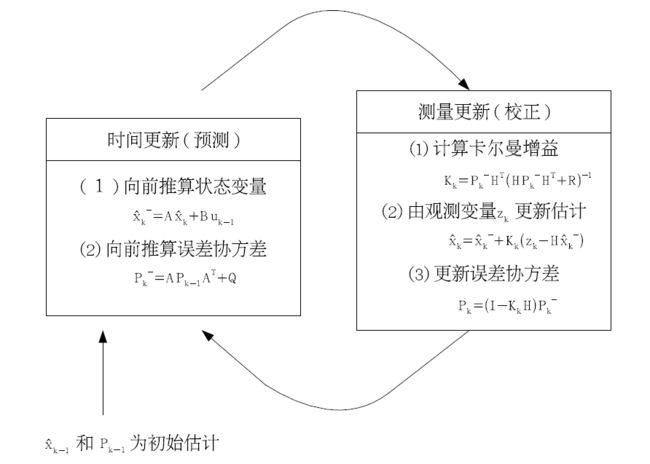
        以下是学习过程中的笔记，略潦草，省略了具体的公式推导，呈现了卡尔曼滤波的基本算法流程（需要事先了解相关概念）。

        找了张图来表示算法流程

        matlab仿真可以看http://blog.csdn.net/heyijia0327/article/details/17667341，因为最近在复习C++，所以用C++写了一个，简陋之处望指正。

        应用背景是匀加速小车，该线性系统的状态差分方程为

        对小车进行建模，ft为合力，小车的状态方程表示为

        矩阵形式表示为

        具体程序如下，某些参数定义见注释。

// Kalme.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include 
#include 
#include 
#include 
#include //包含Eigen矩阵运算库，用于矩阵计算
#include 
#include //用于生成随机分布数列

using namespace std;
using Eigen::MatrixXd;
int _tmain(int argc, _TCHAR* argv[])
{
	//""中是txt文件路径，注意：路径要用//隔开
	ofstream fout("..//result.txt");
	
	double generateGaussianNoise(double mu, double sigma);//随机高斯分布数列生成器函数

	const double delta_t = 0.1;//控制周期，100ms
	const int num = 100;//迭代次数
	const double acc = 10;//加速度，ft/m

	MatrixXd A(2,2);
	A(0,0) = 1;
	A(1,0) = 0;
	A(0,1) = delta_t;
	A(1,1) = 1;

	MatrixXd B(2,1);
	B(0,0) = pow(delta_t,2)/2;
	B(1,0) = delta_t;

	MatrixXd H(1,2);//测量的是小车的位移，速度为0
	H(0,0) = 1;
	H(0,1) = 0;
	
	MatrixXd Q(2,2);//过程激励噪声协方差，假设系统的噪声向量只存在速度分量上，且速度噪声的方差是一个常量0.01，位移分量上的系统噪声为0
	Q(0,0) = 0;
	Q(1,0) = 0;
	Q(0,1) = 0;
	Q(1,1) = 0.01;

	MatrixXd R(1,1);//观测噪声协方差，测量值只有位移，它的协方差矩阵大小是1*1，就是测量噪声的方差本身。
	R(0,0) = 10;

	//time初始化，产生时间序列
	vector time(100, 0);
	for(decltype(time.size()) i = 0; i != num; ++i){
		time[i] = i * delta_t;
		//cout< x_real, rand;
	//生成高斯分布的随机数
	for(int i = 0; i<100;++i){
		MatrixXd a(1,1);
		a(0,0) = generateGaussianNoise(0,sqrt(10));
		rand.push_back(a);
	}
	//生成真实的位移值
	for(int i = 0; i < num; ++i){
		X_real(0,0) = 0.5 * acc * pow(time[i],2);
		X_real(1,0) = 0;
		x_real.push_back(X_real);
	}

	//变量定义，包括状态预测值，状态估计值，测量值，预测状态与真实状态的协方差矩阵，估计状态和真实状态的协方差矩阵，初始值均为零
	MatrixXd X_evlt = MatrixXd::Constant(2,1,0), X_pdct = MatrixXd::Constant(2,1,0), Z_meas = MatrixXd::Constant(1,1,0), 
		Pk = MatrixXd::Constant(2,2,0), Pk_p = MatrixXd::Constant(2,2,0), K = MatrixXd::Constant(2,1,0);
	vector x_evlt, x_pdct, z_meas, pk, pk_p, k;
	x_evlt.push_back(X_evlt);
	x_pdct.push_back(X_pdct);
	z_meas.push_back(Z_meas);
	pk.push_back(Pk);
	pk_p.push_back(Pk_p);
	k.push_back(K);

	//开始迭代
	for(int i = 1; i < num; ++i){
		//预测值
		X_pdct = A * x_evlt[i-1] + B * acc;
		x_pdct.push_back(X_pdct);
		//预测状态与真实状态的协方差矩阵，Pk'
		Pk_p = A * pk[i-1] * A.transpose() + Q;
		pk_p.push_back(Pk_p);
		//K:2x1
		MatrixXd tmp(1,1);
		tmp = H * pk_p[i] * H.transpose() + R;
		K = pk_p[i] * H.transpose() * tmp.inverse();
		k.push_back(K);
		//测量值z
		Z_meas = H * x_real[i] + rand[i];
		z_meas.push_back(Z_meas);
		//估计值
		X_evlt = x_pdct[i] + k[i] * (z_meas[i] - H * x_pdct[i]);
		x_evlt.push_back(X_evlt);
		//估计状态和真实状态的协方差矩阵，Pk
		Pk = (MatrixXd::Identity(2,2) - k[i] * H) * pk_p[i];
		pk.push_back(Pk);
	}
	
	cout<<"含噪声测量"<<"  "<<"后验估计"<<"  "<<"真值"<<"  "<::min();
    const double two_pi = 2.0*3.14159265358979323846;

    static double z0, z1;
    static bool generate;
    generate = !generate;

    if (!generate)
       return z1 * sigma + mu;

    double u1, u2;
    do
     {
       u1 = rand() * (1.0 / RAND_MAX);
       u2 = rand() * (1.0 / RAND_MAX);
     }
    while ( u1 <= epsilon );

    z0 = sqrt(-2.0 * log(u1)) * cos(two_pi * u2);
    z1 = sqrt(-2.0 * log(u1)) * sin(two_pi * u2);
    return z0 * sigma + mu;
}

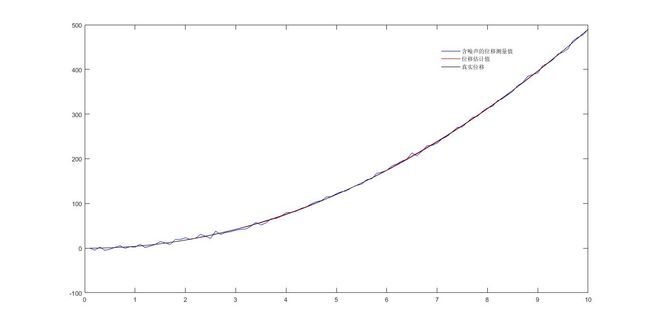
        将数据结果加载到matlab，绘图如下所示，可以看到红色的估计值和黑色的真实值基本吻合，蓝色的为含噪声测量值。

        选一个放大的局部图

        由仿真结果可知，卡尔曼滤波对于含噪声的线性系统具有显著疗效。

注：Eigen矩阵运算库的使用，从官网下载zip压缩包，解压，在工程项目，VC++目录，包含目录中添加解压的文件夹所在目录即可