数据结构之图

本文是数据结构与算法之美的学习笔记

图的概念

图跟树一样也是一种非线性的数据结构，比树更加复杂一点。

树种的元素叫做结点，图中的每个元素叫做顶点，图中的每一个元素都可以与其他的顶点建立连接关系，这种关系叫做边。

比如微信，每个用户就可以叫做一个顶点，两个好友之间的通道就是边，每个用户的好友数量就叫做顶点的度，度表示一个顶点有几条边。

微博跟微信不一样，微博可以单向关注，A关注B，B可以不关注A，这样每个边上就可以有一个箭头了，这种图叫做有向图，没有箭头的叫做无向图。

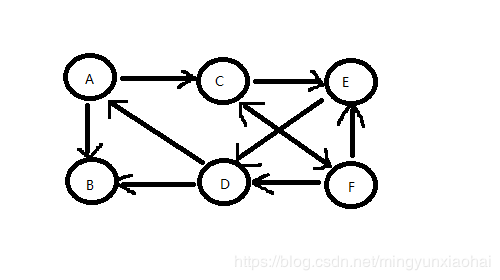
对于有向图，度分为入度和出度，箭头指向自己就是入度，箭头从自己开始指向别的顶点就是出度，对应到微博中就是自己的粉丝和自己关注的人。

如果每条边上都加上权重，这种图就叫做带权图，比如qq空间中的亲密度。

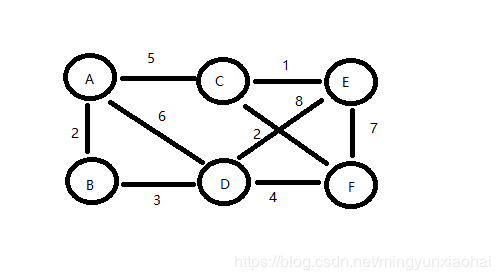
邻接矩阵（Adjacency Matrix）

邻接矩阵是图的一种很直观的存储方法，邻接矩阵的底层依赖的是一个二维数组

• 对于无向图来说，如果如果定点i和定点j之间有一条边，那么A[i][j]和A[j][i]都会标记为1
• 对于有向图来说，比如顶点i指向顶点j，那么A[i][j]就标记为1。
• 对于带权图来说就根据边的权重来填写了。

使用邻接矩阵来存储图的缺点

1. 对于无向图来说，如果A[i][j]为1那么A[j][i]肯定也是1，那么就浪费了一半的存储空间
2. 如果一个图的顶点很多，但是顶点上的边很少，比如微信有几亿用户，每个用户的好友几百几千，这时候使用邻接矩阵那么大部分的空间都浪费了

使用邻接矩阵来存储图的优点

1. 存储简单，在获取两个顶点的关系的时候高效
2. 可以将一些图的运算转换成矩阵的运算

邻接表（Adjacency List）

由于邻接矩阵比较浪费空间，我们可以使用邻接表

邻接表有点像散列表，每个顶点对应一条链表，每个链表中存储了和这个顶点相连的其他的顶点。

邻接矩阵虽然浪费空间，但是查询起来比较快，邻接表节省空间，但是如果我们要知道顶点A是否和顶点B相关联，我们需要遍历顶点B的链表。这其实就是空间换时间或者时间换空间，真实项目中根据实际情况选择使用哪一种。

跟散列表的优化一样，我们可以吧每个顶点对应的链表换成平衡二叉查找树或者跳表等比较高效的数据结构来提升其查找的效率。

使用邻接表实现的一个无向图：

public class Graph { 
  private int v; // 顶点的个数
  private LinkedList<Integer> adj[]; // 邻接表

  public Graph(int v) {
    this.v = v;
    adj = new LinkedList[v];
    for (int i=0; i<v; ++i) {
      adj[i] = new LinkedList<>();
    }
  }

  public void addEdge(int s, int t) { // 无向图一条边存两次
    adj[s].add(t);
    adj[t].add(s);
  }
}

广度优先搜索算法

广度优先搜索算法（Breadth First Search）是一种基于图数据结构的算法，简称BFS，原理很简单就是一层一层的推进，先查找离起始点最近的，然后查找次近的，这样依次往外搜索。

代码实现：

public void bfs(int s, int t) {
  if (s == t) return;
  boolean[] visited = new boolean[v];
  visited[s]=true;
  Queue<Integer> queue = new LinkedList<>();
  queue.add(s);
  int[] prev = new int[v];
  for (int i = 0; i < v; ++i) {
    prev[i] = -1;
  }
  while (queue.size() != 0) {
    int w = queue.poll();
   for (int i = 0; i < adj[w].size(); ++i) {
      int q = adj[w].get(i);
      if (!visited[q]) {
        prev[q] = w;
        if (q == t) {
          print(prev, s, t);
          return;
        }
        visited[q] = true;
        queue.add(q);
      }
    }
  }
}

private void print(int[] prev, int s, int t) { // 递归打印 s->t 的路径
  if (prev[t] != -1 && t != s) {
    print(prev, s, prev[t]);
  }
  System.out.print(t + " ");
}

代码中s代表起始顶点，t代表终止顶点，我们搜索一条从s到t的路径

visited：用来记录已经被访问的顶点，防止顶点被重复访问。

queue：队列，用来存储已经被访问但是其相连接的顶点还没被访问的的顶点，广度优先搜索是一层一层的搜索，queue中记录的也就是我们当前搜索的层中的顶点。

prve: 用来记录搜索路径，比如prve[w]记录的是从哪个前驱顶点遍历过来的。

深度优先搜索算法

深度优先搜索算法（Depth First Search）简称DFS，文中举的例子很形象：走迷宫，走到岔路口就选一个进去，走不通的时候就退回到上一个岔路口，从新选一个入口进入，如此循环直到找到出口。

代码实现：

boolean found = false; // 全局变量或者类成员变量

public void dfs(int s, int t) {
  found = false;
  boolean[] visited = new boolean[v];
  int[] prev = new int[v];
  for (int i = 0; i < v; ++i) {
    prev[i] = -1;
  }
  recurDfs(s, t, visited, prev);
  print(prev, s, t);
}

private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
  if (found == true) return;
  visited[w] = true;
  if (w == t) {
    found = true;
    return;
  }
  for (int i = 0; i < adj[w].size(); ++i) {
    int q = adj[w].get(i);
    if (!visited[q]) {
      prev[q] = w;
      recurDfs(q, t, visited, prev);
    }
  }
}

visited和prev和广度的作用是一样的
found的作用是为了跳出递归的条件。