hdu 6171 Admiral 双向bfs+hash
Admiral
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 153428/153428 K (Java/Others)Total Submission(s): 206 Accepted Submission(s): 54
Problem Description
Suppose that you are an admiral of a famous naval troop. Our naval forces have got 21 battleships. There are 6 types of battleships.
First, we have got one flagship in which the admiral must be and it is denoted by number 0. Others are denoted by number from 1 to 5, each of them has 2, 3, 4, 5, 6 ships of its kind. So, we have got 21 battleships in total and we must take a giant battle against the enemy. Hence, the correct strategy of how to arrange each type of battleships is very important to us.
The shape of the battlefield is like the picture that is shown below.
To simplify the problem, we consider all battleships have the same rectangular shape.
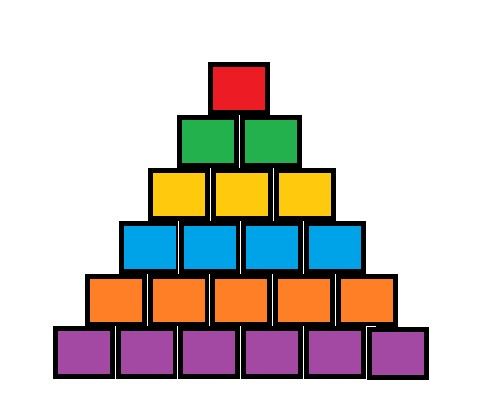
Fortunately, we have already known the optimal state of battleships.
As you can see, the battlefield consists of 6 rows. And we have 6 types of battleship, so the optimal state is that all the battleships denoted by number i are located at the i-th row. Hence, each type of battleship corresponds to different color.
You are given the initial state of battlefield as input. You can change the state of battlefield by changing the position of flagship with adjacent battleship.
Two battleships are considered adjacent if and only if they are not in the same row and share parts of their edges. For example, if we denote the cell which is at i-th row and j-th position from the left as (i,j), then the cell (2,1) is adjacent to the cells (1,0), (1,1), (3,1), (3,2).
Your task is to change the position of the battleships minimum times so as to reach the optimal state.
Note: All the coordinates are 0-base indexed.
First, we have got one flagship in which the admiral must be and it is denoted by number 0. Others are denoted by number from 1 to 5, each of them has 2, 3, 4, 5, 6 ships of its kind. So, we have got 21 battleships in total and we must take a giant battle against the enemy. Hence, the correct strategy of how to arrange each type of battleships is very important to us.
The shape of the battlefield is like the picture that is shown below.
To simplify the problem, we consider all battleships have the same rectangular shape.

Fortunately, we have already known the optimal state of battleships.
As you can see, the battlefield consists of 6 rows. And we have 6 types of battleship, so the optimal state is that all the battleships denoted by number i are located at the i-th row. Hence, each type of battleship corresponds to different color.
You are given the initial state of battlefield as input. You can change the state of battlefield by changing the position of flagship with adjacent battleship.
Two battleships are considered adjacent if and only if they are not in the same row and share parts of their edges. For example, if we denote the cell which is at i-th row and j-th position from the left as (i,j), then the cell (2,1) is adjacent to the cells (1,0), (1,1), (3,1), (3,2).
Your task is to change the position of the battleships minimum times so as to reach the optimal state.
Note: All the coordinates are 0-base indexed.
Input
The first line of input contains an integer T (1 <= T <= 10), the number of test cases.
Each test case consists of 6 lines. The i-th line of each test case contains i integers, denoting the type of battleships at i-th row of battlefield, from left to right.
Each test case consists of 6 lines. The i-th line of each test case contains i integers, denoting the type of battleships at i-th row of battlefield, from left to right.
Output
For each test case, if you can’t reach the goal in no more than 20 moves, you must output “too difficult” in one line. Otherwise, you must output the answer in one line.
Sample Input
1 1 2 0 2 1 2 3 3 3 3 4 4 4 4 4 5 5 5 5 5 5
Sample Output
3
Source
2017 Multi-University Training Contest - Team 10
Recommend
liuyiding | We have carefully selected several similar problems for you: 6181 6180 6179 6178 6177
思路:现场码了半天还是得10多s才能出答案。看了题解,双向bfs。。。感觉我又被套路了。在知道起点和终点的情况下,两边同时bfs能剪掉n多的枝,这个想一下还是想得通的。所以这题就把图hash成字符串(当然你也可以hash成数,6进制不会爆LL,只不过可能写起来不好写),然后两边同时bfs其中一方找到另一方时结束。可能会觉得我的代码风格有点奇怪,因为。。有一些是我叫队友码的,留接口给我用。下面给代码:
#pragma comment(linker, "/STACK:102400000,102400000")
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include