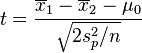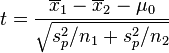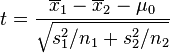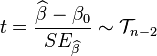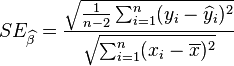概率论:假设检验-t检验、卡方检验和AD-Fuller test
http://blog.csdn.net/pipisorry/article/details/51184556
卡方检验 Chi-Square
the chi-square test measures dependence between stochasticvariables, so using this function “weeds out” the features that are themost likely to be independent of class and therefore irrelevant forclassification.
标称数据的相关性分析,衡量 categorical attributes 相关性的。在特征选择中应该是检验某个单一特征和label之间的相关性,如果独立直接剔除该特征。从上看出有两个方面,一个是:卡法独立性检验,检验两个因素(各有两项或以上的分类)之间是否相互影响的问题,其零假设是两因素之间相互独立。另一个是:卡方拟合性检验,检验单个多项分类名义型变量各分类间的实际观测次数与理论次数之间是否一致的问题,其零假设是观测次数与理论次数之间无差异(就是因素和分类label之间相互独立)。
运用
建立零假说(Null Hypothesis),即认为观测值与理论值的差异是由于随机误差所致;
确定数据间的实际差异,即求出卡方值;
如卡方值大于某特定概率标准(即显著性差异)下的理论值,则拒绝零假说,即实测值与理论值的差异在该显著性水平下是显著的。
[wikipedia]
对应分析
两个分类变量间的关系,无法直接使用常见的皮尔逊相关系数来表述(由于分类型数据的特点,很多基于均值、方差和标准差的分析方法就不太适用了),多采用频数统计、交叉表卡方检验等过程进行处理(面对变量个数少、分类类别少的简单局面,卡方检验和二分类逻辑回归还能够从容应对,一旦变量数量和变量类别多时,分析结果的解读就让人头痛了。),当分类变量的取值较多时,列联表频数的形式就变得更为复杂,很难从中归纳出变量间的关系。对应分析,则是解决分类变量间关系这个复杂问题的有力武器,也称为相应分析(在很多地方也被称为同质性分析或数量化方法),是一种多元统计分析方法,目的是在同时描述各变量分类间关系时,在一个低维度空间中对对应表中的两个分类变量进行关系的描述。
例如,研究全国34个省级行政区居民的收入水平情况,通过抽样收集数据,使用卡方检验能够很容易得出不同省级行政区居民的收入水平分布有显著性差异,但是无法得到北京市高收入居民比例高、云南低收入居民比例低这样具体的结果,也就是无法对分类变量各类别间的相关关系进行清楚展现。对应分析是解决类别相关关系展示很好的方法,它能够将分类交叉表转换为相应的对应分析图,从而使分类结果图形化、直观化。
对应分析原理
对应分析的实质就是将交叉表里面的频数数据作变换以后,展现在散点图上,从而将抽象的交叉表信息形象化。这个变换过程涉及到线性代数的内容,因此在这里就不做数学公式的推导了,草堂君在这里做个形象的解释。
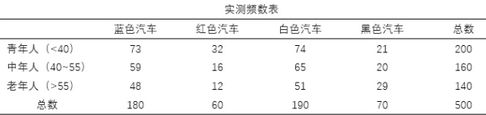
我们以两个分类变量的情况来介绍对应分析的原理。学习过卡方检验的应该知道,卡方检验的实质是将实际的频数分析与期望频数作对比,如果差距很大,超过界限值,那么就可以认为组成交叉表的两个分类变量之间具有相关性。举个例子,某汽车生产企业的市场部收集了某款汽车的销售数据,制成频数交叉表:如果年龄变量与选购的汽车颜色之间没有相关关系,那么这些频数应该是相似的,没有巨大差异,反之,如果这两个分类变量间有相关关系,那么某个或某些单元格里的频数将显著大于其它单元格。
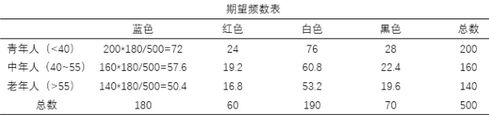
根据上表的数据,可以制作出由期望频数组成的交叉表,期望频数的计算公式为行频数和*列频数和/总频数(参考第一列的计算过程)。卡方检验就将上表的实际频数与下表的期望频数做逐个对比,算出卡方值和检验概率,从而判断两个变量是否有显著性差异。
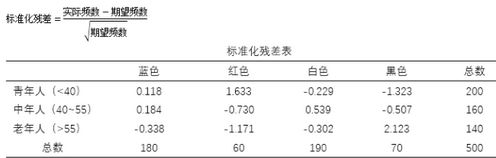
对应分析承接上面两个表格的工作,它首先算出每个单元格的标准化残差,计算公式为:
从上面的公式来看,标准化残差包含了某个年龄段和某种汽车颜色的相关关系信息,相当于相关系数。说到这里,是否想到因子分析。是的,对应分析进行到这里,下一步也是提取标准化残差矩阵(交叉表)的公因子,然后将3个年龄群体和4个汽车颜色放入由公因子(新维度)组成的坐标空间内,通过它们之间的空间距离判断相关性强弱。
[SPSS分析技术:简单对应分析]
[SPSS统计分析案例:对应分析]
某小皮
T检验
T检验,亦称student t检验(Student's t test),学生t检验(英语:Student's t-test)是指虚无假设成立时的任一检定统计有学生t-分布的统计假说检定,属于母数统计。学生t检验常作为检验一群来自常态分配母体的独立样本之期望值的是否为某一实数,或是二群来自常态分配母体的独立样本之期望值的差是否为某一实数。
主要用于样本含量较小(例如n<30),总体标准差σ未知的正态分布资料。常被应用于小样本判断的置信度。分为单总体检验和双总体检验。
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。它与z检验、卡方检验并列。
t检验是戈斯特为了观测酿酒质量而发明的。
前提假设
大多数的t检定之统计量具有t = Z/k的形式,其中Z与k是已知资料的函数。Z通常被设计成对于对立假说有关的形式,而k是一个尺度参数使t服从于t分布。以单样本t检验为例,![]() ,其中
,其中![]() 为样本平均数,
为样本平均数,![]() 为样本数,
为样本数,![]() 为总体标准差。至于k在单样本t检验中为
为总体标准差。至于k在单样本t检验中为![]() ,其中
,其中![]() 为样本的标准偏差。在符合零假说的条件下,t检定有以下前题:
为样本的标准偏差。在符合零假说的条件下,t检定有以下前题:
- Z 服从标准正态分布
- (n - 1)k2 服从自由度(n - 1)的卡方分布
- Z与k互相独立
统计法比较
最常用t检验的情况
- 单样本检验:检验一个正态分布的总体的均值是否在满足零假设的值之内,例如检验一群人的身高的平均是否符合170公分。
- 双样本检验:其零假设为两个正态分布的总体的均值之差为某实数,例如检验二群人的身高之平均是否相等。这一检验通常被称为学生t检验。但更为严格地说,只有两个总体的方差是相等的情况下,才称为学生t检验;否则,有时被称为Welch检验。以上谈到的检验一般被称作“未配对”或“独立样本”t检验,我们特别是在两个被检验的样本没有重叠部分时用到这种检验方式。
- “配对”或者“重复测量”t检验:检验同一统计量的两次测量值之间的差异是否为零。举例来说,我们测量一位病人接受治疗前和治疗后的肿瘤尺寸大小。如果治疗是有效的,我们可以推定多数病人接受治疗后,肿瘤尺寸变小了。
- 检验一条回归线的斜率是否显著不为零。
单样本t检验编辑
检验零假说为一群来自常态分配独立样本xi之母体期望值μ为μ0可利用以下统计量
其中![]() ,
,![]() 为样本平均数,
为样本平均数,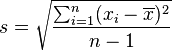 为样本标准偏差,n为样本数。该统计量t在零假说:μ = μ0为真的条件下服从自由度为n − 1的t分布。
为样本标准偏差,n为样本数。该统计量t在零假说:μ = μ0为真的条件下服从自由度为n − 1的t分布。
配对样本t检验编辑
配对样本t检验可视为单样本t检验的扩展,不过检验的对象由一群来自常态分配独立样本更改为二群配对样本之观测值之差。
若二群配对样本x1i与x2i之差为di = x1i − x2i独立且来自常态分配,则di之母体期望值μ是否为μ0可利用以下统计量
其中![]() ,
,![]() 为配对样本差值之平均数,
为配对样本差值之平均数,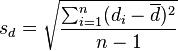 为配对样本差值之标准偏差,n为配对样本数。该统计量t在零假说:μ = μ0为真的条件下服从自由度为n − 1的t分布。
为配对样本差值之标准偏差,n为配对样本数。该统计量t在零假说:μ = μ0为真的条件下服从自由度为n − 1的t分布。
独立双样本t检验编辑
样本数及变异数相等编辑
若二群独立样本x1i与x2i具有相同之样本数n,并且彼此独立及来自二个变异数相等的常态分配,则二群母体之期望值差μ1 - μ2是否为μ0可利用以下统计量
其中![]() ,
,![]() 及
及![]() 为二群样本各自的平均数,
为二群样本各自的平均数,![]() 为样本之共同变异数。该统计量t在零假说:μ1 - μ2 = μ0为真的条件下服从自由度为2n − 2的t分布。
为样本之共同变异数。该统计量t在零假说:μ1 - μ2 = μ0为真的条件下服从自由度为2n − 2的t分布。
样本数不相等但变异数相等编辑
若二群独立样本x1i与x2j具有不相同之样本数n1与n2,并且彼此独立及来自二个变异数相等的常态分配,则二群母体之期望值之差μ1 - μ2是否为μ0可利用以下统计量
其中![]() ,其中
,其中![]() ,
,![]() 及
及![]() 为二群样本各自的平均数,
为二群样本各自的平均数,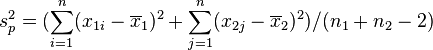 为二群样本共同之变异数。该统计量t在零假说:μ1 - μ2 = μ0为真的条件下服从自由度为n1 + n2 − 2的t分布。
为二群样本共同之变异数。该统计量t在零假说:μ1 - μ2 = μ0为真的条件下服从自由度为n1 + n2 − 2的t分布。
变异数皆不相等编辑
若二群独立样本x1i与x2j具有相等或不相同之样本数n1与n2,并且彼此独立及来自二个变异数不相等的常态分配,则二群母体之期望值之差μ1 - μ2是否为μ0可利用以下统计量
其中![]() ,其中
,其中![]() ,
,![]() 及
及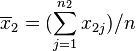 为二群样本各自的平均数,
为二群样本各自的平均数,![]() 及
及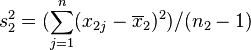 分别为二群样本之变异数。该统计量t在零假说:μ1 - μ2 = μ0为真的条件下服从自由度为
分别为二群样本之变异数。该统计量t在零假说:μ1 - μ2 = μ0为真的条件下服从自由度为
之t分布。这种方法又常称为Welch检验。
简单线性回归之斜率编辑
在简单线性回归的模型
![]()
其中xi,i = 1, ..., n为已知,α与β为未知系数,εi为残差独立且服从期望值0且变异数σ2未知的正态分布,yi,i = 1, ..., n为观测值。我们可以检验回归系数(在此例即为回归式之斜率)β是否相等于特定的β0(通常使β0 = 0以检验xi对yi是否有关联)。
令![]() 与
与![]() 为最小平方法之估计值,
为最小平方法之估计值,![]() 与
与![]() 为最小平方法估计值之标准误差,则
为最小平方法估计值之标准误差,则
在零假设为β = β0的情况下服从自由度为n − 2之t分布,其中
由于 ![]() 为残差(即估计误差),而
为残差(即估计误差),而 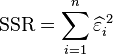 为残差之离均平方和,我们可改写t为
为残差之离均平方和,我们可改写t为
python t-test统计软件
scipy.stats.ttest_ind(a, b, axis=0, equal_var=True)
[scipy.stats.ttest_ind]
皮皮blog
t检验的一个示例
t检验步骤
以单总体t检验为例说明:
问题:难产儿出生体重
n=35, ![]() =3.42,S =0.40,一般婴儿出生体重μ0=3.30(大规模调查获得),问相同否?
=3.42,S =0.40,一般婴儿出生体重μ0=3.30(大规模调查获得),问相同否?
解:
1.建立假设、确定检验水准α
H0:μ = μ0 (零假设,null hypothesis)
H1:μ ≠ μ0(备择假设, alternative hypothesis,)
双侧检验,检验水准:α=0.05
2.计算检验统计量![]()
Note: t统计量计算值为1.77, 自由度为34
3.查相应界值表,确定P值,下结论
查附表,t0.05 / 2(34) = 2.032 #双侧假设检验,即在alpha/2、自由度34下的t值
t < t0.05 / 2(34) #拒绝域是{t>特定值},这样才说明|u-u0|>特定值,也就是u!=u0
P > 0.05
按α=0.05水准,不拒绝H0,两者的差别无统计学意义
[wikipedia-學生t檢驗]
[Richard Mankiewicz, The Story of Mathematics (Princeton University Press), p.158.]
皮皮blog
Augmented Dickey–Fuller test 扩展迪基-福勒检验
用于测试平稳性
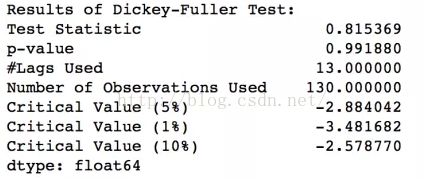
Dickey-Fuller Test: This is one of the statistical tests for checking stationarity. Here the null hypothesis is that the TS is non-stationary. The test results comprise of a Test Statistic and some Critical Valuesfor difference confidence levels. If the ‘Test Statistic’ is less than the ‘Critical Value’, we can reject the null hypothesis and say that the series is stationary. Refer this article for details.
Note: 可以看出这里的拒绝域是{u 用于测试单根 The Augmented Dickey-Fuller test can be used to test for a unit root in a univariate process in the presence of serial correlation. The null hypothesis of the Augmented Dickey-Fuller is that there is a unit root, with the alternative that there is no unit root. If the pvalue is above a critical size, then we cannot reject that there is a unit root. [wikipedia: Augmented Dickey–Fuller test] [python包:statsmodels.tsa.stattools.adfuller] 可以看到,这里最小拒绝H0的alpha值p-value太大,没法拒绝H0,所以This is not a stationary series(H0). [pandas小记:pandas时间序列分析和处理Timeseries ] from: http://blog.csdn.net/pipisorry/article/details/51184556 ref: ADFuller平稳性测试示例
当然同样可以通过the test statistic is way more than the critical values来判断不能拒绝H0(拒绝域是{u