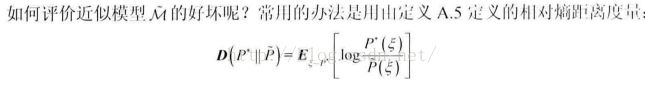机器学习模型的评价指标和方法
http://blog.csdn.net/pipisorry/article/details/52574156
衡量分类器的好坏
对于二类分类器/分类算法,评价指标主要有accuracy, [precision,recall,F-score,pr曲线],ROC-AUC曲线,gini系数。
对于多类分类器/分类算法,评价指标主要有accuracy, [宏平均和微平均,F-score]。
对于回归分析,主要有mse和r2/拟合优度。
二分类模型的评估
机器学习系统设计系统评估标准
- Error Metrics for Skewed Classes有偏类的错误度量精确度召回率
- PrecisionRecall精确度召回率
- Trading Off Precision and Recall权衡精度和召回率F1值
- A way to choose this threshold automatically How do we decide which of these algorithms is best
- Data For Machine Learning数据影响机器学习算法的表现
[Machine Learning - XI. Machine Learning System Design机器学习系统设计(Week 6)系统评估标准 ]
召回率、准确率、F值
对于二分类问题,可将样例根据其真实类别和分类器预测类别划分为:
真正例(True Positive,TP):真实类别为正例,预测类别为正例。
假正例(False Positive,FP):真实类别为负例,预测类别为正例。
假负例(False Negative,FN):真实类别为正例,预测类别为负例。
真负例(True Negative,TN):真实类别为负例,预测类别为负例。
然后可以构建混淆矩阵(Confusion Matrix)如下表所示。
| 真实类别 |
预测类别 |
|
| 正例 |
负例 |
|
| 正例 |
TP |
FN |
| 负例 |
FP |
TN |
准确率,又称查准率(Precision,P):
(1) ![]()
召回率,又称查全率(Recall,R):
![]() (2)
(2)
F1值:
![]() (3)
(3)
F1的一般形式![]() :
:
G-Mean指标,也能评价不平衡数据的模型表现。
ROC-AUC曲线和PRC曲线
[分类模型评估之ROC-AUC曲线和PRC曲线]
KS曲线
柯尔莫哥洛夫-斯米尔诺夫检验(Колмогоров-Смирнов检验)基于累计分布函数,用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。ROC曲线是评判一个模型好坏的标准,但是最好的阈值是不能通过这个图知道的,要通过KS曲线得出。
KS值越大,表示模型能够将正、负客户区分开的程度越大。 通常来讲,KS>0.2即表示模型有较好的预测准确性。
绘制方式与ROC曲线略有相同,都要计算TPR和FPR。但是TPR和FPR都要做纵轴,横轴为把样本分成多少份。 KS曲线的纵轴是表示TPR和FPR的值,就是这两个值可以同时在一个纵轴上体现,横轴就是阈值,然后在两条曲线分隔最开的地方,对应的就是最好的阈值。
下图中,一条曲线是FPR,一条是TPR
吉尼系数Gini coefficient
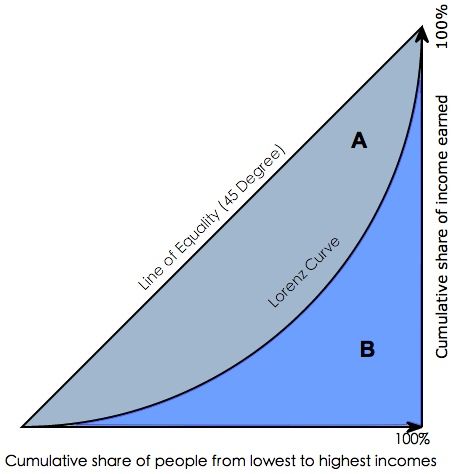
在用SAS或者其他一些统计分析软件,用来评测分类器分类效果时,常常会看到gini coefficient,gini系数通常被用来判断收入分配公平程度,具体请参阅wikipedia-基尼系数。
在ID3算法中我们常使用信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢?CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
Gini coefficient 是指绝对公平线(line of equality)和洛伦茨曲线(Lorenz Curve)围成的面积与绝对公平线以下面积的比例,即gini coefficient = A面积 / (A面积+B面积) 。
用在评判分类模型的预测效力时,是指ROC曲线曲线和中线围成的面积与中线之上面积的比例。
因此Gini coefficient与AUC可以互相转换:
gini = A / (A + B) = (AUC - C) / (A + B) = (AUC -0.5) / 0.5 = 2*AUC - 1
Note: 特别值得注意的一点是,这里的AUC并不是roc_auc(y是二值的)计算里面的那个roc曲线面积,而是指x,y横纵坐标计算出来的面积(y不是二值而是连续值)。
Gini系数的计算
def giniCoefficient(x, y):
'''
gini系数计算
:param x: 推测值(人口)
:param y: 实际值(财富)
'''
x = np.asarray(x)
y = np.asarray(y)
x.__add__(0)
y.__add__(0)
x = np.cumsum(x)
if x[-1] != 0:
x = x / x[-1]
y = np.cumsum(y)
if y[-1] != 0:
y = y / y[-1]
area = metrics.auc(x, y, reorder=True)
gini_cof = 1 - 2 * area
return gini_cof if math.fabs(gini_cof) > pow(math.e, -6) else 0皮皮blog
多分类模型的评估
accuracy
在多类分类的背景下,accuracy = (分类正确的样本个数) / (分类的所有样本个数)。
这样做其实看上去也挺不错的,不过可能会出现一个很严重的问题:例如某一个不透明的袋子里面装了1000台手机,其中有600台iphone6, 300台galaxy s6, 50台华为mate7,50台mx4(当然,这些信息分类器是不知道的。。。)。如果分类器只是简单的把所有的手机都预测为iphone6, 那么通过上面的公式计算的准确率accuracy为0.6,看起来还不错;可是三星,华为和小米的全部预测错了。如果再给一个袋子,里面装着600台galaxy s6, 300台mx4, 50台华为mate7,50台iphone,那这个分类器立马就爆炸了
宏平均(macro-average)和微平均(micro-average)
如果只有一个二分类混淆矩阵,那么用以上的指标就可以进行评价,没有什么争议,但是当我们在n个二分类混淆矩阵上要综合考察评价指标的时候就会用到宏平均和微平均。宏平均(macro-average)和微平均(micro-average)是衡量文本分类器的指标。根据Coping with the News: the machine learning way: When dealing with multiple classes there are two possible ways of averaging these measures(i.e. recall, precision, F1-measure) , namely, macro-average and micro-average. The macro-average weights equally all the classes, regardless of how many documents belong to it. The micro-average weights equally all the documents, thus favouring the performance on common classes. Different classifiers will perform different in common and rare categories. Learning algorithms are trained more often on more populated classes thus risking local over-fitting.
宏平均(Macro-averaging),是先对每一个类统计指标值,然后在对所有类求算术平均值。宏平均指标相对微平均指标而言受小类别的影响更大。即将n分类的评价拆成n个二分类的评价,计算每个二分类的score,n个 score的平均值即为Macro score。
![]() (8)
(8)
微平均(Micro-averaging),是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵,然后计算相应指标。将n分类的评价拆成n个二分类的评价,将n个二分类评价的TP、FP、RN对应相加,计算评价准确率和召回率,由这2个准确率和召回率计算的F1 score即为Micro F1。
[多类分类性能评价之宏平均(macro-average)与微平均(micro-average)]
微平均(包括p\r\f)实际上就是前面说的accuracy,除非pred出了true没有的标签,如[微平均(Micro-averaging)]。
![]() (11)
(11)
从上面的公式我们可以看到微平均并没有什么疑问,但是在计算宏平均F值时我给出了两个公式分别为公式(7)和(8)。都可以用。
[谈谈评价指标中的宏平均和微平均]
在测试数据集上,度量分类器对大类判别的有效性应该选择微平均,而度量分类器对小类判别的有效性则应该选择宏平均。
一般来讲,Macro F1、Micro F1高的分类效果好。Macro F1受样本数量少的类别影响大。
"macro" simply calculates the mean of the binary metrics,giving equal weight to each class. In problems where infrequent classesare nonetheless important, macro-averaging may be a means of highlightingtheir performance. On the other hand, the assumption that all classes areequally important is often untrue, such that macro-averaging willover-emphasize the typically low performance on an infrequent class.
"weighted" accounts for class imbalance by computing the average ofbinary metrics in which each class’s score is weighted by its presence in thetrue data sample.
"micro" gives each sample-class pair an equal contribution to the overallmetric (except as a result of sample-weight). Rather than summing themetric per class, this sums the dividends and divisors that make up theper-class metrics to calculate an overall quotient. Micro-averaging may be preferred in multilabel settings, includingmulticlass classification where a majority class is to be ignored."samples" applies only to multilabel problems. It does not calculate aper-class measure, instead calculating the metric over the true and predictedclasses for each sample in the evaluation data, and returning their(sample_weight-weighted) average.
[Scikit-learn:模型评估Model evaluation]
示例
假设有10个样本,它们属于A、B、C三个类别。假设这10个样本的真实类别和预测的类别分别是:
> 真实:A A A C B C A B B C
> 预测:A A C B A C A C B CKappa一致性系数
交叉表(混淆矩阵)虽然比较粗糙,却是描述栅格数据随时间的变化以及变化方向的很好的方法。但是交叉表却不能从统计意义上描述变化的程度,需要一种能够测度名义变量变化的统计方法即KAPPA指数——KIA。 kappa系数是一种衡量分类精度的指标。KIA主要应用于比较分析两幅地图或图像的差异性是“偶然”因素还是“必然”因素所引起的,还经常用于检查卫星影像分类对于真实地物判断的正确性程度。KIA是能够计算整体一致性和分类一致性的指数。
KIA的计算式的一般性表示为:

总体KAPPA指数的计算式为: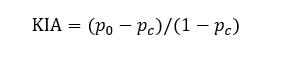
式中, 
式中的p0和pc都有着明确的含义:p0被称为观测精确性或一致性单元的比例;pc被称为偶然性一致或期望的偶然一致的单元的比例。kappa计算结果为-1~1,但通常kappa是落在 0~1 间,可分为五组来表示不同级别的一致性:0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)。
kappa指数计算的一个示例:
混淆矩阵
kappa在sklearn上的实现[sklearn.metrics.cohen_kappa_score¶]
多分类roc曲线
[多分类的ROC曲线]
皮皮blog
回归模型的评估
平均均方误差mse
MSE=1n∑(y¯−yi)2=Var(Y)MSE = \frac{1}{n}\sum(\bar{y}-y_i)^2 = Var(Y)
R^2 (coefficient of determination)
regression score function.评估模型拟合的好坏。训练集估计和学到的模型产生的新数据集评估的偏离度。
在用线性模型拟合完数据之后,我们需要评估模型拟合的好坏情况。当然,这种评估取决于我们想要用这个模型来做什么。一种评估模型的办法是计算模型的预测能力。
在一个预测模型中,我们要预测的值称为因变量(dependent variable),而用于预测的值称为解释变量或自变量(explanatory variable或independent variable)。
通过计算模型的确定系数(coefficient of determination),也即通常所说的R2R^2,来评价模型的预测能力:
R2=1−Var(ε)Var(Y)R^2 = 1 - \frac{Var(\varepsilon)}{Var(Y)}
即1 - 预测模型的mse/数据本身的mse (数据本身的mse就是直接将数据label均值作为预测的mse)
解释R2意义例子
假设你试图去猜测一群人的体重是多少,你知道这群人的平均体重是y¯\bar{y}。如果除此之外你对这些人一点儿都不了解,那么你最佳的策略是选择猜测他们所有人的体重都是y¯\bar{y}。这时,估计的均方误差就是这个群体的方差var(Y):
MSE=1n∑(y¯−yi)2=Var(Y)MSE = \frac{1}{n}\sum(\bar{y}-y_i)^2 = Var(Y)
接下来,假如我告诉你这群人的身高信息,那么你就可以猜测体重大约为α^+β^xi\hat{\alpha}+\hat{\beta}x_i,在这种情况下,估计的均方误差就为Var(ε):
MSE=1N∑(α^+β^xi−yi)2=Var(ε)MSE = \frac{1}{N}\sum (\hat{\alpha}+\hat{\beta}x_i-y_i)^2 = Var(\varepsilon)
所以,Var(ε)/Var(Y)表示的是有解释变量情况下的均方误差与没有解释变量情况下的均方误差的比值,也即不能被模型解释的均方误差占总的均方误差的比例。这样R2表示的就是能被模型解释的变异性的比例。
假如一个模型的R2=0.64R^2=0.64,那么我们就可以说这个模型解释了64%的变异性,或者可以更精确地说,这个模型使你预测的均方误差降低了64%。
在线性最小二乘模型中,我们可以证明确定系数和两个变量的皮尔逊相关系数存在一个非常简单的关系,即:R2=ρ2。
[拟合优度 ]
拟合优度Goodness of fit
拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度。度量拟合优度的统计量是可决系数(亦称确定系数)R^2。R^2最大值为1。R^2的值越接近1,说明回归直线对观测值的拟合程度越好;反之,R^2的值越小,说明回归直线对观测值的拟合程度越差。
皮皮blog
其它
学习目标
{评价学习模型的不同方法}
不同的模型通过表达了不同的折中方案。近似模型根据一种性能度量可能表现很好,但根据其它度量又可能很差。为了引导学习算法的发展,必须定义学习任务的目标,并且定义能够评价不同结果 相应的度量方法。
密度估计
评价指标及方法
期望的对数似然
由于生成分布p*是固定的,评价指标——相对熵可以转换成最大期望的对数似然。直观上就是,M~对从真实分布中采样的点赋予的概率越大,越能反映它是该分布。
数据的似然
专栏:16.A 用于设计和评价机器学习过程的基本实验性条款
评价泛化性能
抵抗测试holdout-testing
Dtrain: 目标函数;Dtest: 损失函数。
k-折交叉验证
讨论及及算法
选择学习过程
使用抵抗测试或交叉验证来选择学习过程。更好的是使用训练集,用来学习模型;验证集,用来评价学习过程的不同变体并从中做出选择;分离的测试集,用来在其上评价最终的性能(会使分割数据的问题更加恶化)。也可以发展一种嵌套的交叉验证方案。
专栏:16.B 用来尝试并回答有关模型类合适复杂性问题的基本理论框架:PAC界
[《Probabilistic Graphical Models:Principles and Techniques》(简称PGM)]
from: http://blog.csdn.net/pipisorry/article/details/52574156
ref: [Scikit-learn:模型评估Model evaluation ]
[Scikit-learn:模型评估Model evaluation 之绘图 ]