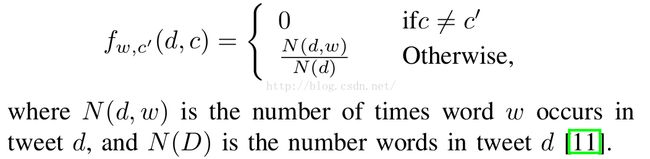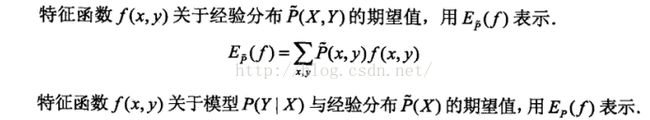最大熵模型The Maximum Entropy：模型

http://blog.csdn.net/pipisorry/article/details/52789149

最大熵模型相关的基础知识

[概率论：基本概念CDF、PDF ]

熵定义为：   [信息论：熵与互信息 ]

[最优化方法：拉格朗日乘数法 ]

[参数估计：贝叶斯思想和贝叶斯参数估计 ]

[参数估计：最大似然估计MLE ]

皮皮blog

 

最大熵原理和思想

        最大熵原理是在1957 年由E.T.Jaynes 提出的，其主要思想是，在只掌握关于未知分布的部分知识（即定义的特征函数）时，应该选取符合这些知识但熵值最大的概率分布（而LR模型只是一个特例，特征函数固定为X=x，且p(y|x)为正态分布？）。因为在这种情况下，符合已知知识的概率分布可能不止一个。我们知道，熵定义的实际上是一个随机变量的不确定性，熵最大的时侯，说明随机变量最不确定，换句话说，也就是随机变量最随机，对其行为做准确预测最困难。从这个意义上讲，那么最大熵原理的实质就是，在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，这是我们可以作出的唯一不偏不倚的选择，任何其它的选择都意味着我们增加了其它的约束和假设，这些约束和假设根据我们掌握的信息无法做出。

[北大常宝宝 《自然语言处理的最大熵模型》]

        学习概率模型时，在所有可能的概率模型分布中，熵最大的模型就是最好的模型。“熵最大的模型或者说“等可能性”的模型就是最好的模型”。因为为了准确的估计随机变量的状态，我们一般习惯性最大化熵，认为在所有可能的概率模型（分布）的集合中，熵最大的模型是最好的模型。换言之，在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，其原则是承认已知事物（知识），且对未知事物不做任何假设，没有任何偏见。例如，投掷一个骰子，如果问"每个面朝上的概率分别是多少"，你会说是等概率，即各点出现的概率均为1/6。因为对这个"一无所知"的色子，什么都不确定，而假定它每一个朝上概率均等则是最合理的做法。从投资的角度来看，这是风险最小的做法，而从信息论的角度讲，就是保留了最大的不确定性，也就是说让熵达到最大。

最大熵模型的直觉示例

        假设随机变量X有5个取值{A, B, C,D, E}，要估计各个值的概率P(A), P(B), P(C), P(D), P(E)

         解：

                   这些概率值满足以下约束条件：

                            P(A)+ P(B) + P(C) + P(D) + P(E) = 1

                   在没有其他约束条件的情况下，根据“最大熵原理”，最合理的判断就是所有取值的概率相等，即：

                            P(A)= P(B) = P(C) = P(D) = P(E) = 1/5

                   有时，我们能从一些先验知识中得到一些约束条件，如：

                            P(A)+ P(B) = 3/10

                            P(A)+ P(B) + P(C) + P(D) + P(E) = 1

                   那根据“最大熵原理”，最合理的判断就是所有A和B取值的概率相等，C、D、E平分剩下的概率，即：

                            P(A)= P(B) = 3/20

                            P(C)= P(D) = P(E) = 7/30

                   以此类推。

约束条件

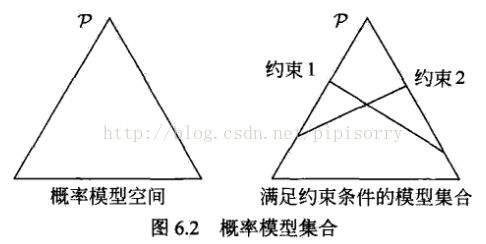
        通常用约束条件来确定概率模型的集合，所以，最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。

约束的几何解释

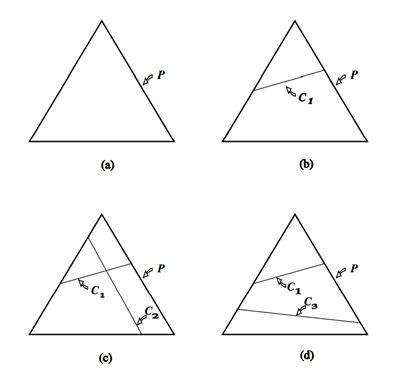
Note: 下面具体解释一个这种限制的几何解释。这里，P是三点上所有可能的概率分布空间。如果我们不施加任何约束（图a），所有概率模型都是允许的。施加一个线性约束C1后，模型被限制在C1定义的区域，如图b示。如果两个约束是可满足的, 施加第二个线性约束后可以准确确定p（c1c2交叉点确定了一个概率分布P），如图c所示。另一种情形是，第二个线性约束与第一个不一致，例如，第一个约束可能需要第一个点的概率是1/3，第二个约束需要第三个点的概率是3/4，图d所示。在目前的设置中，线性约束是从训练数据集中抽取的，不可能手工构造，因此不可能不一致。进一步来说，在我们应用中的线性约束甚至不会接近唯一确定的p,就象图c那样。相反，集合中的模型是无穷的（所以上面也说到“这样的模型仍然有无穷多个”，因此最大熵模型除了约束外，还需要一个特定的熵最大，这个后面会讲到）。

[几何解释 Adam Berger. A Brief Maxent Tutorial. 1996.]

[wikipedia: 单纯形]

 

 

最大熵模型The Maximum Entropy

        最大熵原理是统计学习的一般原理，将它应用到分类得到最大熵模型。

最大熵模型的问题和任务

最大熵模型的约束条件

经验分布及其具体形式

 

特征函数

 

特征函数的具体设计

语言模型（如语音识别）

       Usual features are n-grams, but it is easy to integrate any information source, for example triggers or syntactic features [1].

[1] R. Rosenfeld, “A maximum entropy approach to adaptive statistical language modeling,” Computer, Speech and Language, vol. 10, pp. 187–228, 1996.

文本分类

        features are usually initiated as

特征示例

 

约束条件（n个）

Note: 1 ：p(x)是近似的：

2： 有n个特征函数就有n个约束条件：

最大熵模型熵的定义

最大熵模型(Maximum Entropy Modeling)

　i. 给定一个训练样本集，我们希望寻找一个分布符合如下两个条件：
　　1. 满足已知的约束条件（satisfies the input constraints）
　　2. 最大化其不确定性（maximizes the uncertainty）

 

Note: 到这里，我们还没有给出最大熵模型p(y|x)的求解，只是给出了最大熵模型带有约束的表征形式。下节讲具体形式推导[最大熵模型The Maximum Entropy：学习]。

 

最大熵模型的评价

       最大熵模型的优点：首先，最大熵统计模型获得的是所有满足约束条件的模型中信息熵极大的模型；其次，最大熵统计模型可以灵活地设置约束条件，通过约束条件的多少可以调节模型对未知数据的适应度和对已知数据的拟合程度（即最大熵模型可以使用任意的复杂相关特征，在性能上最大熵分类器超过了Byaes分类器）；再次，它还能自然地解决了统计模型中参数平滑的问题。

        最大熵模型的不足：首先，最大熵统计模型中二值化特征只是记录特征的出现是否，而文本分类需要知道特征的强度，因此，它在分类方法中不是最优的；其次，由于算法收敛的速度较慢，所以导致最大熵统计模型它的计算代价较大，时空开销大；再次，数据稀疏问题比较严重。和Byaes分类器一样，有一个共同的缺点：每个词都是单独进行分类的，标记之间的关系无法得到充分利用，具有马尔可夫链的HMM模型可以建立标记之间的马尔 可夫关联性，这是最大熵模型所没有的。

        最大熵模型是适定的well-defined, 即其解存在且唯一。可以利用相对熵和毕达哥拉斯性质等进行证明，在推导学习过程中也可以看出这种证明。[北大常宝宝 《自然语言处理的最大熵模型》]

最大熵模型和神经网络的区别和联系

        standard neural network language model has a very similar form. The main difference is that the features for this model are automatically learned as a function of the history. Also, the usual features for the ME model are binary, while NN models use continuous-valued features.

NN LM：

        maximum entropy models are very close to neural network models with no hidden layer. The maximum entropy model can be seen in the context of neural network models as a weight matrix that directly connects the input and output layers.

        In fact, a neural network model with no hidden layer can learn a bigram language model [9], which is similar to what was shown for the maximum entropy models. However, in [9], the memory complexity for bigram model was V^2 , where V is size of the vocabulary. For a trigram model and V around 100k, it would be infeasible to train such model.

[2011 Mikolov, Tomáš, et al. "Strategies for training large scale neural network language models." ASRU 2011.]

from: http://blog.csdn.net/pipisorry/article/details/52789149

ref: [数学之美 吴军]

[52nlp MIT自然语言处理第五讲：最大熵和对数线性模型（第一部分）]

[北大常宝宝 《自然语言处理的最大熵模型》]

[张学文 最大熵方法]

[最大熵学习笔记]*

code[最大熵模型介绍及实现]