SO-Net论文阅读笔记（1）SOM

SO-Net论文阅读笔记（1）SOM

这是CVPR2018新出来的论文，大体看了一下，里面用的想法和之前写的PointCNN有神似之处，挺赶兴趣的，于是就精读一下。markdown对图片的支持真的难受，凑合一下吧。

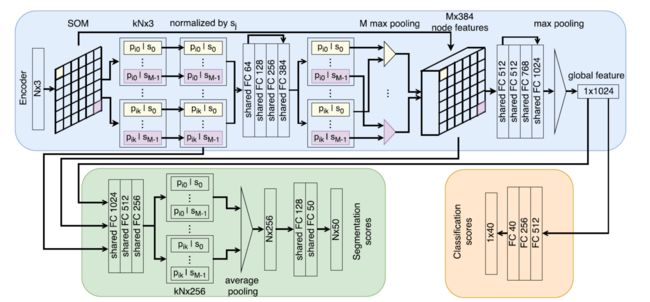
这是整体的网络结构，我们来一点一点分析。

1. SOM 自组织竞争网络

  最底层（最前面）的SOM被用于产生点云数据的低维表示（在这篇文章里是2维）。使用的学习方法是无监督竞争学习，而不是反向传播。但是原始的训练方法不是排列不变的，换句话说当输入数据顺序变化时，学习的结果是不同的。作者认为这主要时两个原因导致的：
- 训练结果与SOM节点的初始化高度相关，换句话说不同的初始参数会产生不同结果
- 依赖于单个样本的更新方法与输入样本的顺序相关

  根据这两个特点，为了使得SOM对输入数据的排序适应采用的策略是：
- 初始化时不再采用随机初始化，而采用固定的参数配置
- 在计算完所有点之后再进行参数更新

  因为点云数据三个轴都被标准化到[-1, +1]的区间内，所以采用某一个初始化方法，将节点初始化到这个区域内即可。作者在这里说可以采用简单的potential field来生成初始猜测，这里不太理解具体是什么方法，等到分析具体算法再说。而采用batch update的原因，作者说这样做的更新对某一给定点云是决确定的，还引用了一个参考文献《自组织映射》，估计里面应该有这个结论的数学证明，先放着当结果用。

  因为SOM采用的是无监督学习，所以这部分的计算完全是和后面的计算分开的，完全可以先把这部分研究明白，再去分析后面的网络，一点一点来嘛。先上一个作者做出来的事例图

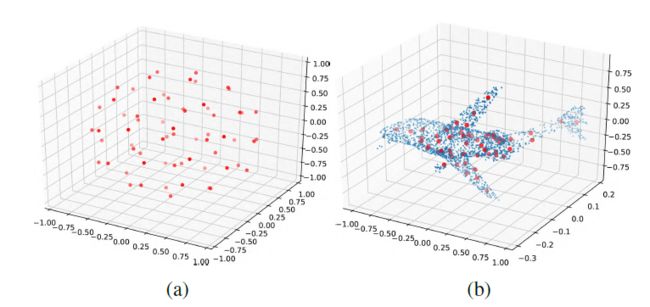
   a是初始化的结果，b是节点训练完成之后的节点分布情况

   论文的附录D部分更加详细的描述了作者实现SOM的算法。

1.1 SOM节点初始化

   除了要对排序拥有不变性之外，初始化还必须要防止学习结果陷入局部最小值。次优结果的SOM可能使得节点被孤立的隔离在点云之外（这里不知道作者是怎么得到这个结论的）。为简单起见，作者采用的是固定节点的初始化方法。用均匀分布生成一组节点的坐标作为节点的初始值（这里的均匀分布只的是概率分布里的均匀分布，不是真的均匀排开）。不幸的是，作者实验发现产生个别分离于点云之外的点是不可避免的，这些节点的权值将被置为0。作者又说实验发现网络的鲁棒性能够适应少量这样的点。
   作者用来初始化节点的具体方法是势场法

Alogithm 1： Potential field method for SOM initialization 基于势场法的SOM初始化

S S 是 M M 个SOM节点（坐标）组成的集合 S={sj∈R3,j=0,...,M−1} S = { s j ∈ R 3 , j = 0 , . . . , M − 1 } M=m∗m M = m ∗ m

   作者解释说，算法的核心是使节点之间相互排斥，同时外加力量使节点趋向初始位置，λ是节点之间斥力及趋向初始位置的权重。注意到算法运行的整个过程只用到了 sj s j ，而 sj s j 是用随机数生成的，这就意味着整个计算和输入无关，这说明这个算法使用来初始化节点位置的。接下来还有学习算法。
   分析这个算法，若将λ设置为0，则 fnodej f j n o d e 将恒为0，参数更新退化为 sj←sj+ηfwallj s j ← s j + η f j w a l l , 而 fwallj=−sj f j w a l l = − s j ,于是式子便退化为:

sj←sj−ηsj=(1−η)sj s j ← s j − η s j = ( 1 − η ) s j

   即 sj s j 会以指数衰减，最终收敛到0，所以可以理解为所有点会向圆点收缩。
   如果λ不为0，原式子可以化为：

sj←(1−η)sj+ηλ∑ksj−sk||sj−sk||  (j≠k) s j ← ( 1 − η ) s j + η λ ∑ k s j − s k | | s j − s k | |     ( j ≠ k )

   第一项为收缩，第二项为由其他点指向节点j的方向向量之和，将其加到 $s_j$意味着j节点向远离其他节点的方向移动。
   由此可知，学习率 η η 越大，向原点收缩的速度越快， ηλ η λ 越大，点与点之间排斥性越强，最后收敛的结果也就越发散。所以 λ λ 最终决定收敛的形状。

实验结果与论文里给出的图还是有一定区别的，论文的图中初始化时比较像球，但是调整几次参数之后发现当刚好把所有点限制在[-1, +1]之内时的参数残生的结果和球差距还是比较大的，可能是论文中还采用了什么trick。不过应该对最终结果影响不是很大。

1.2 批量参数更新

   与SOM逐点更新不同，批量更新在再计算完点云中所有点的结果后进行更新。就导致每次的更新和输入点的顺序无关。在SOM训练期间，每个训练样本影响获胜的神经元和其拓扑邻域内的神经元。定义邻域的函数是高斯分布函数。

P P 和 S S 分别代表输入点集和SOM节点集，学习率 ηt η t 和邻域半径参数 (σx,σy) ( σ x , σ y ) 随时间逐渐下降，这也符合传统的做法。

   实验结果：逐点实现出来时候计算速度挺慢的，毕竟点云数据量还是挺大的。不过这个算法是可以并行的，并行之后速度应该能提升不少