Unity之Vector3.Slerp球形插值原理介绍

先看API：
public static Vector3 Slerp(Vector3 a, Vector3 b, float t);
介绍：通过t数值在from和to之间插值。返回的向量的长度将被插值到from到to的长度之间。
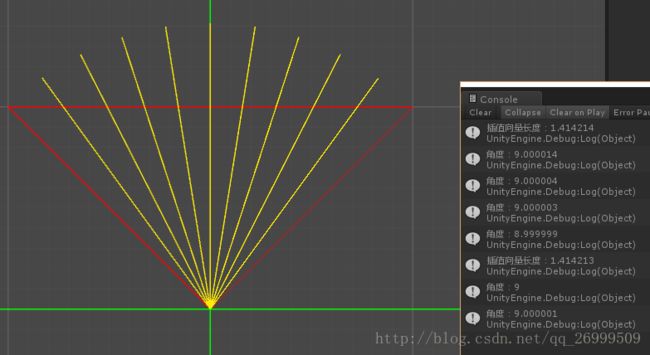
先上一个示意图：

上图的代码如下：

    private Vector3 mStart = new Vector3(-1, 1, 0);
    private Vector3 mEnd = new Vector3(1, 1, 0);

    // Update is called once per frame
    private void Update()
    {
        //绘制坐标轴
        Debug.DrawLine(new Vector3(-100, 0, 0), new Vector3(100, 0, 0), Color.green);
        Debug.DrawLine(new Vector3(0, -100, 0), new Vector3(0, 100, 0), Color.green);
        Debug.DrawLine(new Vector3(0, 0, -100), new Vector3(0, 0, 100), Color.green);

        Debug.DrawLine(Vector3.zero, mStart, Color.red);
        Debug.DrawLine(Vector3.zero, mEnd, Color.red);
        Debug.DrawLine(mStart, mEnd, Color.red);
        for (int i = 1; i < 10; ++i)
        {
            Vector3 drawVec = Vector3.Slerp(mStart, mEnd, 0.1f * i);
            Debug.DrawLine(Vector3.zero, drawVec, Color.yellow);

        }
    }

下面先做几次实验来验证下面两个猜想：
1、猜想一：插值的向量的长度是均匀线性变化的
2、猜想二：插值的向量之间的角度是一样大的

上图验证：
实验一：我们在上面代码的基础上加上输出：

//加在for循环里
Debug.Log("插值向量长度："+ drawVec.magnitude);
Debug.Log("角度：" + Vector3.Angle(drawVec, mStart) / i);

我们发现虽然有误差，但是猜想基本成立，我们修改mStart和mEnd两向量继续实验。

实验二：mStart = (-1,0,0) mEnd = (0,3,4)

从上面可以看出两个猜想成立

这里额外要验证一个问题，就是当两个向量为平行向量时，结果如下，下面直接看图：
（1）mStart = (-1, 0, 0) mEnd = (1, 0, 0)

（2）mStart = (-1, 1, 0) mEnd = (1, -1, 0)

（3）mStart = (-1, 1, 1) mEnd = (1, -1, -1)

那么现在就可以利用这几个结论来自实现Slerp插值了。

下面直接上代码：
代码关键内容如下：
（1）旋转向量函数
（2）旋转矩阵

    /// 

    /// 两个向量的球形插值
    /// 
    /// 向量a
    /// 向量b
    /// t的值在[0..1]
    /// 
    public static Vector3D Slerp(Vector3D a, Vector3D b, float t)
    {
        if (t <= 0)
        {
            return a;
        }
        else if (t >= 1)
        {
            return b;
        }

        Vector3D v = RotateTo(a, b, Vector3D.Angle(a, b) * t);

        //向量的长度，跟线性插值一样计算
        float length = b.magnitude * t + a.magnitude * (1 - t);
        return v.normalized * length;
    }

    /// 

    /// 将向量from向向量to旋转角度angle
    /// 
    /// 
    /// 
    /// 
    /// 
    public static Vector3D RotateTo(Vector3D from, Vector3D to, float angle)
    {
        //如果两向量角度为0
        if (Vector3D.Angle(from, to) == 0)
        {
            return from;
        }

        //旋转轴
        Vector3D n = Vector3D.Cross(from, to);

        //旋转轴规范化
        n.Normalize();

        //旋转矩阵
        Matrix4x4 rotateMatrix = new Matrix4x4();

        //旋转的弧度
        double radian = angle * Math.PI / 180;
        float cosAngle = (float)Math.Cos(radian);
        float sinAngle = (float)Math.Sin(radian);

        //矩阵的数据
        //这里看不懂的自行科普矩阵知识
        rotateMatrix.SetRow(0, new Vector4(n.x * n.x * (1 - cosAngle) + cosAngle, n.x * n.y * (1 - cosAngle) + n.z * sinAngle, n.x * n.z * (1 - cosAngle) - n.y * sinAngle, 0));
        rotateMatrix.SetRow(1, new Vector4(n.x * n.y * (1 - cosAngle) - n.z * sinAngle, n.y * n.y * (1 - cosAngle) + cosAngle, n.y * n.z * (1 - cosAngle) + n.x * sinAngle, 0));
        rotateMatrix.SetRow(2, new Vector4(n.x * n.z * (1 - cosAngle) + n.y * sinAngle, n.y * n.z * (1 - cosAngle) - n.x * sinAngle, n.z * n.z * (1 - cosAngle) + cosAngle, 0));
        rotateMatrix.SetRow(3, new Vector4(0, 0, 0, 1));

        Vector4 v = Vector3D.ToVector4(from);
        Vector3D vector = new Vector3D();
        for (int i = 0; i < 3; ++i)
        {
            for (int j = 0; j < 3; j++)
            {
                vector[i] += v[j] * rotateMatrix[j, i];
            }
        }
        return vector;
    }

    /// 

    /// 将一个Vector3D转换为Vector4
    /// 
    /// 
    /// 
    public static Vector4 ToVector4(Vector3D v)
    {
        return new Vector4(v.x, v.y, v.z, 0);
    }

    public Vector3 ToVector3()
    {
        return new Vector3(x, y, z);
    }

这里暂时没有对两个向量共线反向的情况进行说明，不过主要实现已经给出来了。但是，我发现一点问题，看图：
（1）v1 = new Vector3(0, 2, 0);v2 = new Vector3(5, 0, 0);

ok，正常

（2）v1 = new Vector3(3, 0, 0);v2 = new Vector3(0, 0, 5);

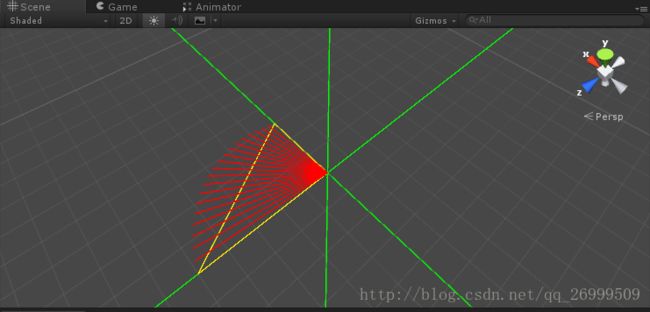
ok，正常

（3）在RotateTo函数中，数据不精确导致存在误差，也就是我打印v1和v2的叉乘 （图中黄色） 与 （图中红色向量）的叉乘 存在误差，这样其实就是该函数的旋转轴不准确。

以上猜想以及代码实现 没有找到权威认证，如有异议，欢迎探讨。。。

补充：
自己无聊利用Slerp插值画了下面这个图，纯属娱乐。。。

以上知识分享，如有错误，欢迎指出，共同学习，共同进步。