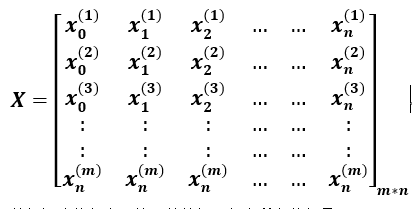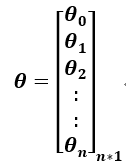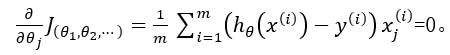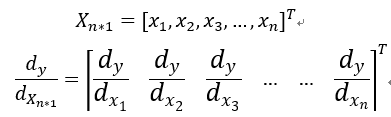一、监督学习(supervised-learning)与无监督学习(unsupervised-learning)
1.监督学习中数据集是由给定的正确答案组成,目的是训练机器预测更多的答案。如:房价预测、肿瘤判定、垃圾邮件判定。
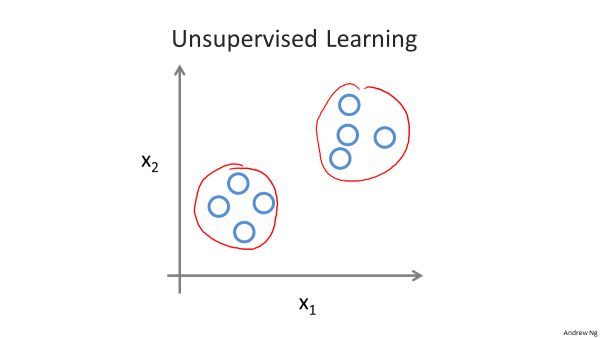
2.无监督学习中人工不对数据集作任何说明,不给答案,不贴标签,目的是让机器自动将一堆混乱的数据分成几个簇(类),而分类的标准没有事先
· 给出。例如:新闻分类、自动市场分割、前景与背景声音分割。
二、回归问题(regression)与分类问题(classification)
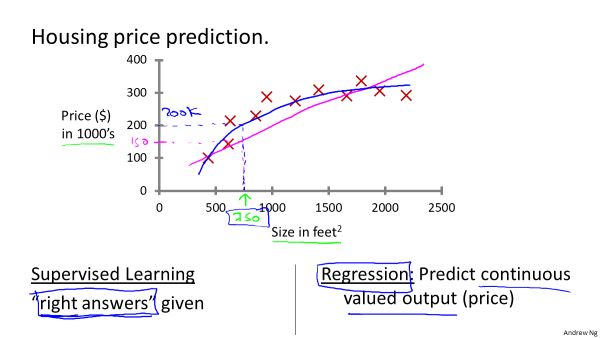
1.回归与分类都属于监督学习。
2.回归问题的输出是连续量,例如房价预测。
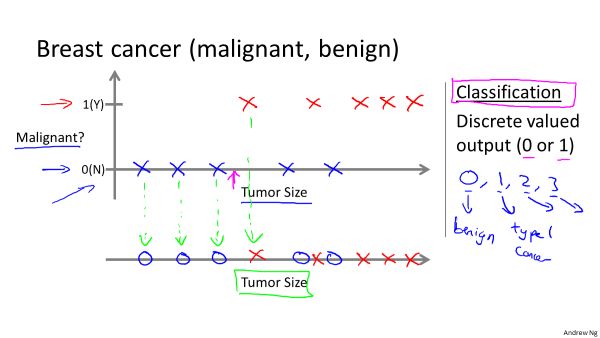
3.分类问题的输出是离散变量,例如肿瘤鉴定。
三、线性回归(linear regression)
1.符号定义
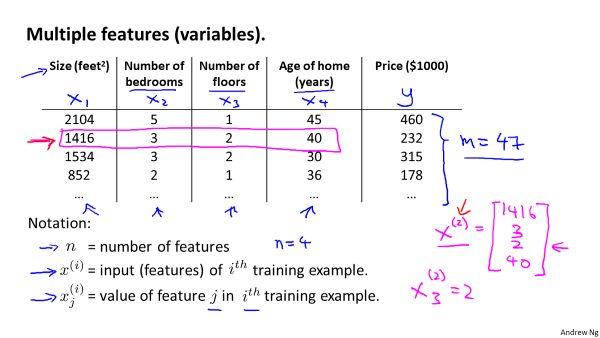
M:数据量(图中一行为一份数据);
X:特征输入,Xj^((i))表示第i行数据第j个特征量;
Y:目标输出,为一个列向量;
θ:模型参数;
hθ (x): 假设函数(Hypothesis),如:![]()
2.代价函数(cost function)

公式表示每一份数据的预测值与实际值之间偏差的平方之和,再取均值。代价越小,拟合越好。
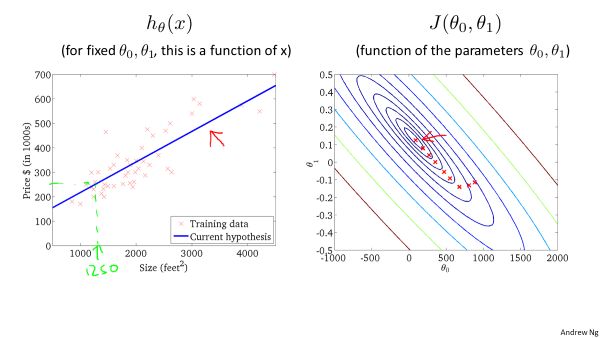
只有一个模型参数时,代价函数是一个一元二次函数,当有两个模型参数时,代价函数分布如下:
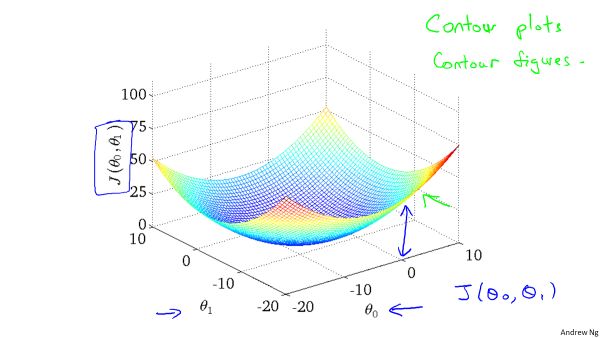
用等高线图表示,每个等值线表示代价相同,越接近中心,代价越小:
3.梯度下降法(gradient descent)
沿梯度方向更新模型参数,最终达到局部最低点。但当特征较多时,更多时候取得是局部最小值。
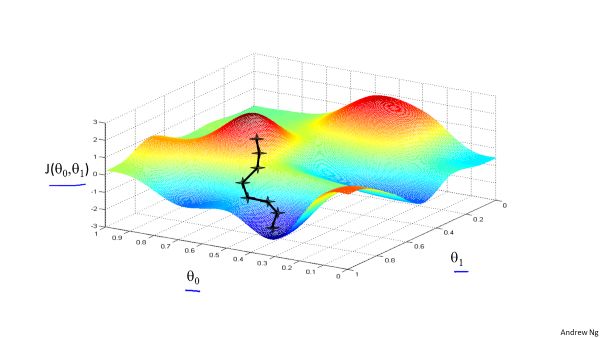
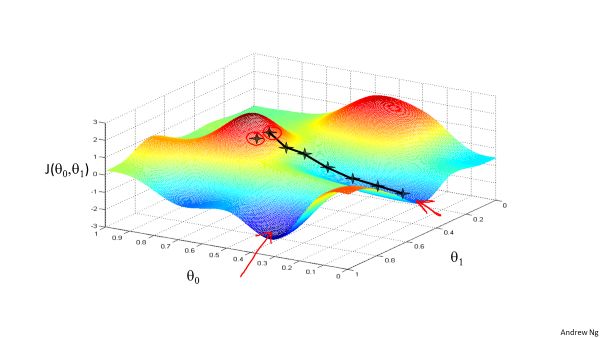
更新方程:
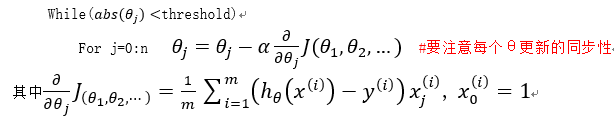
α为学习率,他的大小决定了达到最优解的快慢。如果α太小,迭代的次数就会很多,但最终迭代结果越精确;而如果α太大,一开始会很快接近最优解,
但在最优解附近震荡,甚至代价函数值会越来越大。一般需要对迭代结果进行检查,以确保算法的正确以及学习率的合理性,可以绘制iteration-J曲线图
进行调试。或者,采用动态学习率,在接近收敛时学习率可以自动变小。
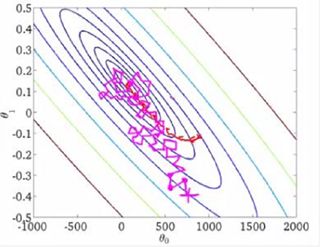
梯度下降主要有BATCH梯度下降和随机梯度下降,前者在计算代价函数时采用全部数据,这在数据量十分大时计算量非常大,因此常采用后者,取部分数据
计算代价函数。两者迭代过程分别如下:
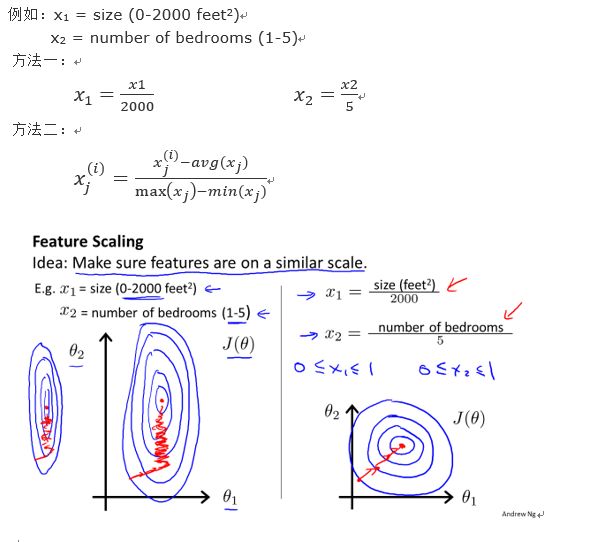
4.特征缩放(feature scaling)
当多个特征的取值相差的数量级较大时,等高线被过分拉长,会导致迭代次数增加,降低算法效率,
因此在处理多元线性回归时要特征缩放,将特征的值统一到(-1,1)附近。
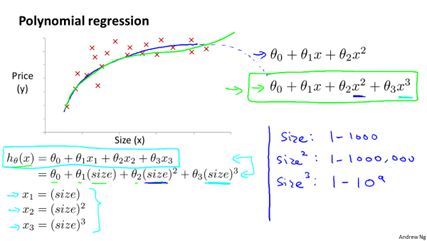
5.多项式回归(polynomial scaling)
普通的线性回归,拟合出来的都是一条直线,有时候并不能很好地贴合数据。例如在房价预测中,假设特征只有size,那么我们自己可以定义
第二特征为(size)^2,甚至定义第三特征(size)^3。那么假设函数仍是各特征的线性函数,但却原始特征size的三次函数了。
6.方程的矩阵表示
♦数据矩阵
数据矩阵的行表示第i份数据,包含所有特征量;
数据矩阵的列表示某个特征的所有数据,其中x_n^((m))=1。
♦系数矩阵
系数矩阵每行对应一个特征;
♦输出矩阵
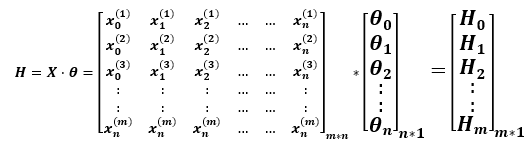
♦方程的矩阵表示
7.正规方程(normal equation)
我们的目标是寻求代价函数的最小值,那么可以求使一阶偏导为0的点。即:
![]()
采用正规方程法,不需要再设定学习率,过程自动化了很多,并且这里是不需要特征缩放的;在特征个数n比较小的时候,效率高于梯度下降法;
但当n比较大(万级),就不如梯度下降法了。并且正规方程法对后面的许多算法也不适用。在运用正规化方程式,可能会碰到数据举证不可逆的
情况,原因主要有两点:有两个以上的特征线性相关。样本数少,而特征量过多(如m=10,n=100)。
8.矩阵向量求导
参考博客:https://www.cnblogs.com/pinard/p/10750718.html
关于矩阵向量求导,主要有以下9种情况:
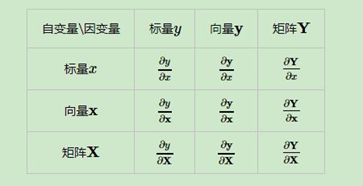
为了清晰区分标量、向量与矩阵,用小写表示标量。大写表示向量与矩阵,并且写出它们的下标。关于求导布局,有分子布局和分母布局两种,一般
标量对向量矩阵求导采用分母布局,向量矩阵对标量求导采用分子布局,向量对向量求导采用分子布局。总结起来就是分子是向量或矩阵,就采用分子布局。
♦向量或矩阵对标量求导
假设有一系列标量对同一标量求导:

将这一系列标量排列为向量,所以向量矩阵对标量求导就是向量矩阵的每个元素都对标量求导,求完后再按分子布局排列,矩阵对标量求导也类似。
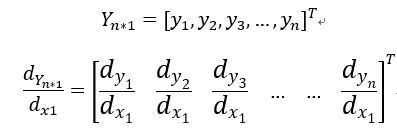
♦标量对向量或矩阵求导
♦向量对向量求导
就是对向量Y中的每个元素,它要对向量X中的每个元素都求遍导,求导结果为一个矩阵,由于采用分子布局,则矩阵的列与Y列数相同,行与X
的列数的相同。
如果是列向量对行向量求导,结果矩阵同上;
如果是行向量Y_(1*m)对列向量X_(n*1)求导,结果维度为n*m。
9.微分法求解矩阵向量的导数
参考博客:https://www.cnblogs.com/pinard/p/10791506.html
♦微分与导数的关系
对于含多变量的函数的微分,有以下结论:
![]()
将变量x,y,z整合为向量的形式:
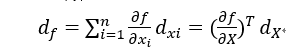
也就是说标量对向量的导数与它的向量微分存在一个转置关系。这样我们可以通过间接求微分来求导数。为了统一向量微分和矩阵微分,公式改为:
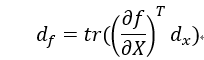
Tr为迹,等于主对角元素之和,那么标量的迹等于它本身。
♦矩阵微分的性质
♦迹的性质