tensorflow实战自学【三】

卷积神经网络初步

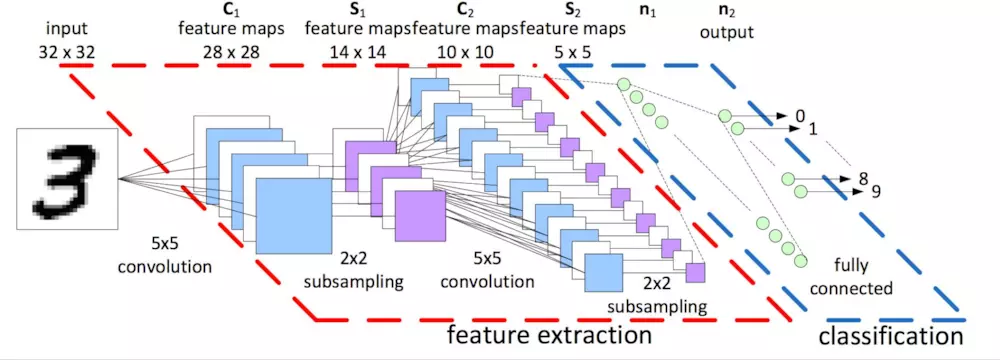
原理简介

在【一】里面利用单层感知机简单实现了图像识别的功能，但错误率依旧相对较高。考虑这是由于将二维图片展开成一维向量后丢失了图片在二维空间上的空间信息。参考人识别图片的过程，人脑并不是直接读取整张图片的信息，而是先提取局部重要信息，例如看一张人的全身照时，我们可能不会在意图片的全部信息，而是会看局部信息，看脸，身材，穿着。卷积神经网络便是如此考虑的，拿到一张图片时，利用卷积核逐步提取局部信息，生成新的图像矩阵。此时的卷积核，即过滤器矩阵，也就是我们想要训练的参数之一。

卷积

下面是网上盗了张gif
(原po地址：https://blog.csdn.net/v_july_v/article/details/51812459）
以下图来阐述如何做卷积。

上图展示的是一张通道为3的图片，一般是指彩色图片，黑白图片的通道为1。整个$w_0$算作一个filter，整个$w_2$算作一个filter。故上图展示的是，一层卷积层，此卷积层有两个filter，对一张3通道的图片做卷积，卷积后得到的是一张具有2通道的图片。计算过程为，逐个按位相乘，然后对矩阵里的元素全部求和，最后三个矩阵得到的和再相加。
例如，（怕加号混淆，故暂不考虑偏置项$b_0$）$(x[:3,:3,0]\ast w_0[:,:,0]+x[:3,:3,1]\ast w_0[:,:,1]+x[:3,:3,2]\ast w_0[:,:,2])$，这儿的矩阵相乘是按元素相乘，而不是矩阵乘法，上述公式得到的矩阵再对所有元素求和，得到的一个标量便为filter $w_0$对图片x的局部$x[:3,:3,:]$做卷积得到的结果。

池化

卷积操作过后一般会接上一个池化操作，池化一般分为平均池化与最大池化，可以将池化理解为从一张图片的众多局部信息里提取出突出的特征，并且降低维度。

平均池化，即是在将整张图片分为各个小矩阵后，对每个小矩阵里的元素求平均值，然后用这个平均值代替此小矩阵，从而实现了保留特征且降低维度的效果。而最大池化即是用小矩阵中的最大值来代替小矩阵。
在整个网络中卷积与池化操作完成后，会对得到的多通道图片进行flatten，然后与下一层神经元进行全连接，最后接上softmax层。

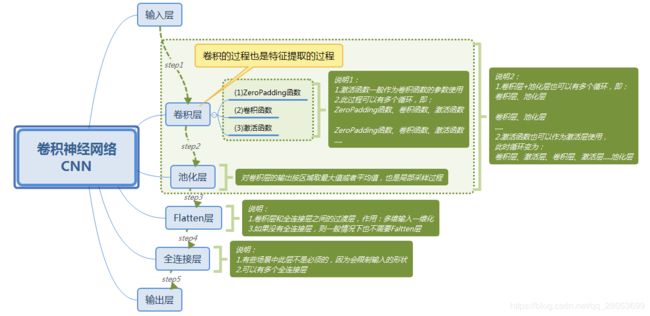
全流程

相关函数

tf.nn.conv2d(input,filter,strides,padding,use_cudnn_on_gpu=True,data_format=‘NHWC’,dilations=[1, 1, 1, 1],name=None)

计算给定的4-D input和filter张量的2-D卷积。给定形状为[batch, in_height, in_width, in_channels]的输入张量和形状为[filter_height, filter_width, in_channels, out_channels]的滤波器/内核张量,此操作执行以下操作：
将滤镜展平为具有形状[filter_height * filter_width * in_channels, output_channels]的二维矩阵。从输入张量中提取图像补丁，以形成形状为[batch, out_height, out_width, filter_height * filter_width * in_channels]的虚拟张量。对于每个补丁,右对乘滤波器矩阵和图像补丁矢量。
详细说明,使用默认的NHWC格式,

output[b, i, j, k] =
    sum_{di, dj, q} input[b, strides[1] * i + di, strides[2] * j + dj, q] *
                    filter[di, dj, q, k]

必须有strides[0] = strides[3] = 1。对于相同水平和顶点步幅的最常见情况，strides = [1, stride, stride, 1]。
参数：
input：一个Tensor，必须是下列类型之一：half,bfloat16,float32,float64；一个4-D张量，维度顺序根据data_format值进行解释，详见下文。
filter：一个Tensor，必须与input相同，形状为[filter_height, filter_width, in_channels, out_channels]的4-D张量。
strides：ints列表，长度为4的1-D张量，input的每个维度的滑动窗口的步幅；维度顺序由data_format值确定，详见下文。
padding：string，可以是：“SAME”, “VALID”，要使用的填充算法的类型。
use_cudnn_on_gpu：bool，默认为True。
data_format：string，可以是"NHWC"，“NCHW”，默认为"NHWC"；指定输入和输出数据的数据格式；使用默认格式“NHWC”，数据按以下顺序存储：[batch, height, width, channels]；或者，格式可以是“NCHW”，数据存储顺序为：[batch, channels, height, width]。
dilations：ints的可选列表,默认为[1, 1, 1, 1]，长度为4的1-D张量，input的每个维度的扩张系数；如果设置为k> 1，则该维度上的每个滤镜元素之间将有k-1个跳过的单元格；维度顺序由data_format值确定，详见上文；批次和深度尺寸的扩张必须为1。
name：操作的名称(可选)。
返回：
一个Tensor，与input具有相同的类型。

tf.nn.max_pool(value,ksize,strides,padding,data_format=‘NHWC’,name=None)

在输入上执行最大池化。
参数：
value：由data_format指定格式的4-D Tensor。
ksize：具有4个元素的1-D整数Tensor。输入张量的每个维度的窗口大小。
strides：具有4个元素的1-D整数Tensor。输入张量的每个维度的滑动窗口的步幅。
padding：一个字符串，可以是’VALID’或’SAME’。填充算法。
data_format：一个字符串.支持’NHWC’,‘NCHW’和’NCHW_VECT_C’。
name：操作的可选名称。
返回：
由data_format指定格式的Tensor.最大池输出张量。

代码实现部分

实现思路

主要阐述卷积神经网络部分
读入的每张图片数据为一个一维的向量（shape=(784)），先将此向量转变为2维形式的向量，即矩阵。接着做第一次卷积与池化，注意卷积过后需要先使用激活函数激活，此处采用的是ReLu激活函数，激活函数后便使用最大池化提取主要特征并降维。第一层卷积采用的卷积核为[5,5]的矩阵，一共有32个卷积核，卷积核的滑动步长为[1,1,1,1]，实际意义为不会遗漏每个点，padding=‘SAME’，指要进行边界填充。滑动步长小于卷积核的维度有一个好处就是对于图像矩阵中的点，我们能够重复采集，提高了每个点的复用率。对于最大池化，我们选择将图像中每个[2,2]的小矩阵降维为一个数，同样padding=‘SAME’，进行边界填充。因为第一次卷积时卷积核有32个，故卷积后通道为1的黑白图片会变为通道为32的图片，故在第二次卷积时，需要注意图片通道的设定。第二次卷积我们依旧采用[5,5]大小的卷积核，一共使用64个卷积核对图片进行卷积操作，再激活，之后最大池化照旧。两次卷积池化过后，将得到的图片展开为一维向量，接上一个有1024个神经元的全连接层，激活函数激活，再与最后一层输出层连接之间考虑dropout操作，提升神经网络的泛化性能。输出层含有10个神经元，对应着0~9。损失函数考虑使用交叉熵。
训练过程，每个batch包含50个样本数据，一共训练20000个batch，在训练过程中使dropout的keep_prob=0.5，验证过程设为1，即全保留。

代码

# -*- coding: utf-8 -*-
"""
Created on Tue Jul 23 09:17:20 2019

@author: Administrator
"""

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import ssl
ssl._create_default_https_context = ssl._create_unverified_context

mnist=input_data.read_data_sets('MNIST_data/',one_hot=True)
sess=tf.InteractiveSession()

x = tf.placeholder("float", [None, 784])
y_ = tf.placeholder("float", [None,10])
sess=tf.InteractiveSession()
def weight_variable(shape):#生成初始filter
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)

def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)

def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],strides=[1, 2, 2, 1], padding='SAME')

W_conv1 = weight_variable([5, 5, 1, 32])#filter大小为[5,5]，图片通道为1，filter数量为32
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1,28,28,1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])

h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])

y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

sess.run(tf.initialize_all_variables())
for i in range(20000):
    batch = mnist.train.next_batch(50)
    if i%100 == 0:
        train_accuracy = accuracy.eval(feed_dict={x:batch[0],y_:batch[1],keep_prob:1.0})
        
        print("step %d, training accuracy %g"%(i, train_accuracy))
    train_step.run(feed_dict={x:batch[0],y_:batch[1],keep_prob:0.5})

print("test accuracy %g"%accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))