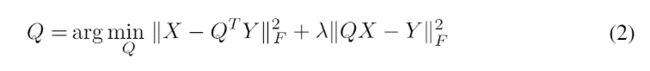《Class label autoencoder for zero-shot learning》阅读笔记

一、解决的问题

现有的零样本学习（ZSL）方法通常在训练已知类或测试未知类中学习feature space到semantic embedding space（文本或属性空间）之间的映射关系。

但是，由于多语义嵌入空间具有用于描述同一类的不同语义信息的多样性特征，在特征空间和多语义嵌入空间之间不能使用映射函数。

我的理解是：在同一类别中，可能存在多个语义描述，即语义描述与类别之间是多对一的关系！这正是我目前面临的难题。

但是读完发现并不是很清楚这篇论文的相关解法。

为了解决这个问题，该文章提出了一种基于学习类标签自动编码器（learning class label autoencoder， CLA）的ZSL新方法。CLA不仅可以构建一个统一的框架来适应多语义嵌入空间，而且可以构造编码器 - 解码器机制来约束特征空间和类标签空间之间的双向投影。

为了减轻领域漂移（Domain Shift）问题，存在两个挑战：

• 一种是如何利用语义信息对知识转移关系进行建模；
• 另一种是如何构建视觉特征与多语义信息之间的投影函数

二、主要贡献

• 用于ZSL中的多语义信息，基于自动编码器机制在特征和类标签空间之间构造投影函数的一种新思想。
• 通过不同流形结构的演化关系挖掘来提高未知类的识别的可行方法（已知类的特征分布结构，未知类的特征分布结构，未知类和未知类之间的语义分布结构）。Other is a feasible method presented to improve unseen classes recognition by the evolution relationship mining of the different manifold structure(the feature distribution structure of seen classes,the feature distribution structure of unseen classes, the semantic distribution structure between seen and unseen classes). 

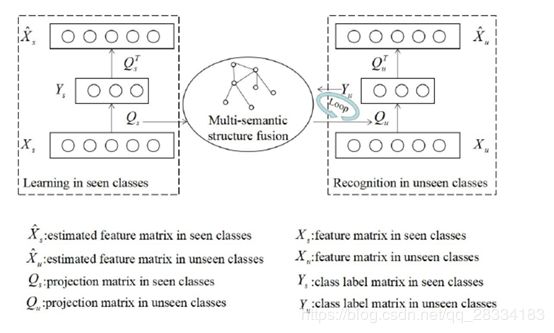
三、CLA模型

1、Linear autoencoder

将自动编码器机制扩展到类标签空间，并用语义信息直接将视觉特征编码到类标签。给定，输入数据是视觉特征矩阵X（d×N阶）并且可以通过变换矩阵Q（k×d阶）投影到k维类标签空间中。类标签表示为Y（k×N）。根据自编码器，类标签表示可以通过变换矩阵Q *（d×k）映射回X^（d×N）。Q * = QT

我们可以等效地将（1）重新表述为无约束优化问题，如下所述。

这里，λ是用于平衡编码器和解码器的权衡参数。

2、ZSL Model

在ZSL中，视觉特征包括两组，

即已知类的特征矩阵Xs（d×Ns），类标签矩阵Ys（ks×Ns）；

未知类的特征矩阵Xu（d×Nu），没有类标签矩阵Yu（ku×Nu）。语义特征集可以定义为S = {Ss，Su}，其中Ss（ds×ks）或Su（ds×ku）。

我们期望在考虑多语义信息的情况下，在已知类中学习到的变换矩阵Qs（ks×d），将知识转移到未知类的变换矩阵Qu（ku×d）。因此，我们想要找到Qs和Qu之间的关系。为此，我们分别定义了以下公式。

这里，Ws（ks×ks）（ks是已知类的数量）是已知类的相似矩阵，是已知类的结构表示。因为As（ks×d）是用于编码所见类的投影矩阵。通过上式，我们可以将Qs分解为两个部分，其中Ws描述了已知类的本质特征，而As可以提取已知类中的一般信息。在未知类中，公式如下：

这里，Wu（ku×ku）（ku是未知类的数量）是未知类的相似矩阵，是未知类的结构表示。Au（ku×d）用于编码未知类的投影矩阵。可以分解Qu为两部分，其中Wu描述了未知类的本质特征，而Au提取了未知类中的一般信息。为了描述已知类和未知类之间的一般信息的转移关系，我们定义了以下公式。

在这里，Au不是通过自动编码器机制直接获得的。因此，我们通过As和Wsu（ks×ku）计算了Au，它是相似矩阵，并在已知类和未知类之间传递一般信息。在公式（3），（4）和（5）中，可以如下计算相似度矩阵。

在这里，当zi和zj分别是已知类中的视觉类特征或语义类表示时，wij是Ws的元素;虽然zi和zj在未知类中是可视类特征或语义类表示，但wij是Wu的元素;如果zi和zj分别是视觉类特征或语义类表示在看到或看不见的类中，wij是Wsu的元素。根据上述定义，我们可以等效地重新制定公式（2）的类别如下。

为了优化公式（8），我们可以将其转换为众所周知的西尔维斯特方程（附录A显示了细节）。Bartels-Stewart算法[49]可以通过运行Matlab函数“sylvester”来有效地解决这个问题。当我们获得As时，Aucan由式（3）和（5）计算。就式（4）而言，Yucan可通过以下公式计算。

我们可以通过以下公式确定估计的标签y到xu∈Xuby。

3、Multi-semantic structure evolution fusion

在公式（8），（9）和（10）中，相似矩阵（Ws，Wu，Wsu）可以通过公式（6）计算。如果我们可以获得多语义信息，则语义信息的结构可以通过下面的公式中的多相似性矩阵的线性关系来建模。

在这里，M是多语义信息的数量。αi是相似矩阵的线性系数，即W（s，i）（在已知类中的第i个语义信息的结构表示），W（u，i）（第i个语义信息在未知类中的结构表示）或W（us，i）（在已知类和未知类之间的第i个语义信息的结构表示）。

除了多语义信息之外，视觉特征还可以帮助构建对象类的结构表示（一种方法很容易通过平均具有相同标签的所有视觉特征来描述视觉类）。但是，我们只通过公式（10）知道未知类的标签。换句话说，我们期望通过估计标签来计算视觉特征类的结构表示。因此，上述相似度矩阵不仅来自语义信息，还来自视觉上的特征存在。我们重新制定公式（11）如下。

在这里，W（s，I），W（u，I）和W（su，I）分别是已知类，未知类以及已知和未知类之间的视觉特征类的结构表示。W（s，I）因为已知类中的标签是确定的，而W（u，I）和W（su，I）是动态变化的，在未知类中有估计的标签。因此，我们分别使用β= [β1β2...βM+ 1] T和γ= [γ1γ2...γM+ 1] T来对不同结构表示进行加权。我们可以用公式（12）表示公式（8）。

为了优化公式（13），我们优化β来优化As将其转换为一个众所周知的Sylvester方程（附录A显示细节），然后通过线性编程来解决β。我们可以通过公式（9）和（10）获得初始估计的标签。初始估计标签可能不准确，因此可以呈现演化过程以通过迭代计算来重新确定模型的性能。因此，我们可以通过估计的标签更新W（u，I）和W（su，I）。为了更新γ，我们构造公式（14）约束标签的正向传播。

公式（14）约束标记的正向传播.γ=argminγ（kMXi =1γiW（u，i）-γM+ 1W（u，I）k2F +δkMXi=1γiW（su，i）-γM+ 1W（su，I）k2F）=argminγ（kγTPuk2F+δkγTPsuk2F）stM + 1Xi =1γi= 1（14）这里，W（u，i）和W（u，I）的元素形成Pu∈R的列（M + 1）×（ku×ku），而W（su，i）和W（su，I）的元素使得Psu∈R（M + 1）×（ks×ku）的列.Formula（14）可以转换为求解γ的线性规划。演化过程可以通过迭代计算在公式（12），（9），（10）和（14）中实现。

为了描述CLA的细节，我们在算法1中演示了所提出的CLA算法的伪代码，包括三个步骤。第一步（第1行和第2行）初始化了看不见的类的结构表示和结构关系。第二步（第3行和第4行）计算融合结构，用于计算所见类的投影矩阵并更新结构关系。第三步（从第6行到第11行）是一个演化过程，用于通过迭代计算重新确定看不见的类的分类性能。此外，进化过程还可以融合其他ZSL方法的识别结果，以进一步提高看不见的类的分类性能。

实验

数据集

我们在四个具有挑战性的数据集中评估了建议的方法cla，其中包括具有属性的动物（awa）[17]、幼鸟-200-2011（cub）[50]、斯坦福犬（狗）[51]和ILSVRC2012/ILSVRC2010（IMNET-2）[1]。在IMNET-2中，与[7]中相同的配置是1000个类的ILSVRC2012用于Seen类，360个类的ILSVRC2010用于UnSeen类。这些数据集可分为五个类别：zsl的细粒度识别（cub和dogs）或非细粒度识别（awa和imnet-2）。表1显示了这些数据集的统计信息和提取的特征（第4.2节中图像和语义特征的详细信息）。

Image and semantic feature

图像和语义特征描述是建立zsl模型的必要条件。由于在大尺度数据库的基础上，利用图像特征来捕捉物体的识别特征，采用图像特征作为经过预训练的GoogleNet[24][5]的输出（1024维特征向量），这是处理整个图像输入的端到端范式。语义特征可以通过四种方法在不同的数据集中提取。第一种方法是从属性（att）[9]中获取特征向量，该属性由人类在awa和cub中的注释和判断得出。第二种方法是通过预测两层神经网络[52]上的文本文档中的单词来提取单词向量（W2V），这些神经网络分别位于awa、cub、imnet-2和dogs中。第三种方法是获得手套（GLO）形式的词汇共现统计数据，该数据来自于一个大型的未标记文本语料库[53]，该语料库位于awa、cub和dogs中。第四种方法从矢量类结构中获得层次嵌入（hie），用于描述awa、cub和dogs中的类层次关系（例如wordnet[24][54]）。Classification and validation protocols

可以通过平均所有测试类精度来计算分类精度。在学习模型中，有三个参数，即λ（权衡参数和公式（13），P（算法1中的总迭代次数）和δ（权衡参数和公式（14））。根据训练类集和测试类集之间的比例，将训练类集交替分为学习集和验证集。我们得到λ对应于最佳结果通过交叉验证在0.001,0.01,0.1,1,10,100,1000,10000中。在所有实验中，Pisset为50且δ等于0.1。