数据结构——之算法以及算法时间复杂度和算法空间复杂度
算法(Algorithm)
算法是指令的集合,是为解决特定问题而规定的一系列操作。
它是明确定义的可计算过程,以一个数据集合作为输入,并产生一个数据集合作为输出。
一个算法通常来说具有以下五个特性:
- 输入:一个算法应以待解决的问题的信息作为输入。
- 输出:输入对应指令集处理后得到的信息。
- 可行性:算法是可行的,即算法中的每一条指令都是可以实现的,均能在有限的时间内完成。
- 有穷性:算法执行的指令是有限的,每个指令又是在有限时间内完成的,因此整个算法也是在有限时间内可以结束的。
- 确定性:算法对于特定的合法输入,其对应的输出是惟一的。即当算法从一个特定输入开始,多次执行统一指令集结果总是相同的
简单来说,算法就是计算机解题的过程。在这个过程中,无论是形成解题的思路还是编写程序,都是在实施某种算法。前者是算法的逻辑形式,后者是算法的代码形式。
举例:如何求 1 + 2 + 3 + ... + 100 = ?
算法1:依次相加
算法2:高斯算法(首尾相加 * 50)
算法3:使用递归实现:sum(100) = sum(99) + 100,sum(99) = sum(98) + 99 ... sum(2) = sum(1) + 2,sum(1) = 1
评价算法的优劣依据:复杂度(时间复杂度和空间复杂度)
算法的复杂性体现在运行该算法所需资源的多少上,计算机资源最重要的是时间和空间资源,因此复杂度分为时间和空间复杂度
时间复杂度是指执行算法所需要的计算工作量;
空间复杂度是指执行该算法所需要的内存空间。
时间复杂度(Time Complexity)定义
时间频度:一个算法执行所消耗的时间,从理论上是不可能计算出来的,必须上机运行测试才能知道。但是我们不可能也没有必要对每个算法都上机测试。
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。
一个算法中的语句执行次数称为语句频度或时间频度,表示 T(n) ,n 表示问题的规模。
时间复杂度:用于描述问题的规模
但是有时我们想知道他变化时呈现什么规律,想知道问题的规模,而不是具体的次数,此时引入时间复杂度。
一般情况下,算法中基本操作重复执行的次数是问题规模 n 的摸个函数,用 T(n) 表示,若有某个辅助函数,f(n) 使得当 n 趋近于无穷大时,T(n)/f(n) 的极限值不等于 0 的常数,则称 f(n) 是 T(n) 的同数量级函数。
记作 T(n) = O(f(n)) ,称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度:T(n) = O(f(n))
或者说:时间复杂度就是时间频度去掉低阶项和首项常数。
注意:时间频度与时间复杂度是不同的,时间频度不同,但是时间复杂度可能相同。
比如:某两个算法的时间频度是 T(n) = 100000n^2 + 10n ,T(n) = n^2
但是时间复杂度都是 T(n) = O(n^2)
最坏时间复杂度和平均时间复杂度
最坏情况下的时间复杂度称为最坏时间复杂度。一般不特别说明,讨论时间复杂度均是最坏的情况下的时间复杂度。
这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界,这就保证了算法的运行时间不会比任何更长。在最坏的情况下的时间复杂度为T(n) = O(n) ,它表示对于任何输入实例,该算法的运行时间不可能大于O(n)。
时间复杂度的计算:
其实根本没有必要计算时间频度,即使计算处理还要忽略常量、低次幂和最高次幂的系数,所以可以采用如下算法:
1. 找出算法中的基本语句:算法中执行次数最多的那条语句就是基本语句,通常是最内层的循环体。
2. 计算基本语句的执行次数的数量级:只需计算基本语句执行次数的数量级,这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可,可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析,并时注意力集中在最重要的一点上:增长率。
3. 用大O记号表示算法的时间性能:将基本语句执行次数的数量级放入大O记号中。
时间复杂度计算举例:
一个简单的时间复杂度为O(1)
int count = 0;
T(n) = 1
T(n) = O(n)
100个简单语句的时间复杂度也是O(1).(100是常数,不是趋于无穷大的n)
int count = 0;
T(n) = 1
T(n) = O(n)
一个循环的时间复杂度是O(n)
int n = 8,count = 0;
for(int i = 1; i <= n; i ++){
count ++;
}
T(n) = n;
T(n)=O(n)
时间复杂度为O(log2️⃣n)的循环语句
int n = 8,count = 0;
for(int i = 1; i <= n; i *= 2){
count ++;
}
T(n) = log2️⃣n
T(n) = O(log2️⃣n)
时间复杂度为O(n^2)的二重循环
int n = 8,count = 0;
for(int i = 1; i <= 100n; i ++){
for(int j = 1; j <= 10n; j ++){
count ++;
}
}
T(n) = 100n * 10n = 1000n^2
T(n) = O(n^2)
时间复杂度为O(nlog2️⃣n) 的二重循环
int n = 8,count = 0;
for(int i = 1; i <= n; i *= 2){
for(int j = 1; j <= n; j ++){
count ++;
}
}
里循环 n ci,外循环 log2️⃣n 次
T(n) = n * log2️⃣n
T(n) = O( nlog2️⃣n)
时间复杂度为 O(n^2)的二重循环
int n = 8,count = 0;
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= i; j ++){
count ++;
}
}
需要复杂数学运算:T(n) = 1 + 2 + 3 +... + n = (n+1)*n/2 时间复杂度是 O(n^2);
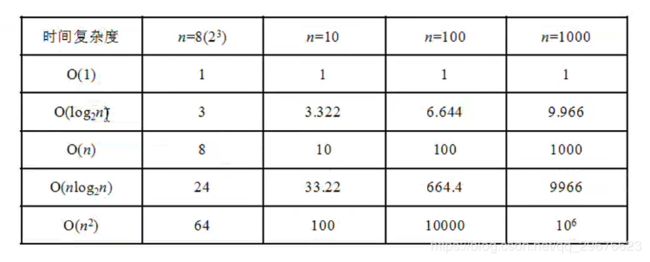
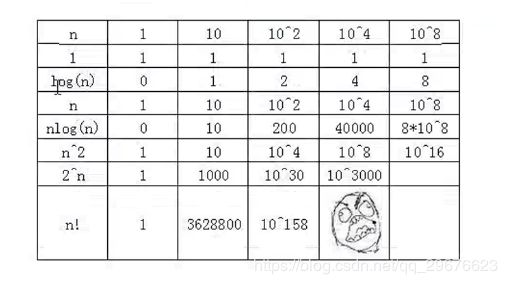
常用的时间复杂度:
常数阶 O(1)
对数阶 O(log2️⃣n)
线性阶 O(n)
线性对数阶 O(n*log2️⃣n)
平方阶 O(n^2)
立方阶 O(n^3)
...
k次方阶 O(n^k)
指数阶 O(2^n)
阶乘阶 O(n!)
上述时间复杂度级别,执行效率越来越低。
空间复杂度(Space Complexity)
算法的存储量包括:
1. 程序本身所占空间
2. 输入数据所占空间
3. 辅助变量所占空间
输入数据所占空间只取决于问题本身,和算法无关,则只需要分析除输入和程序之外的辅助变量所占额外空间。
空间复杂度是对一个算法在运行过程中临时占用的存储空间大小的度量,一般也作为问题规模 n 的函数,以数量级形式给出,记作:S(n) = O(g(n))
空间复杂度分析1:
int function(int n){
int i,j,k,s;
s = 0;
for(int i = 0; i <= n; i ++){
for(int j = 0; i <= i; j ++){
for(int k = 0; k <= j; k ++){
s ++;
}
}
}
}
由于算法中的临时变量的个数与问题规模 n 无关,所以空间复杂度均为 S(n) = O(1).
空间复杂度2:递归算法
S(n) = O(n).