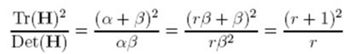SIFT算法描述
本博文下载地址:http://pan.baidu.com/s/1geTrV5D
SIFT特征提取算法流程:
1、 输入图像
2、 多尺度空间极值点检测
3、 关键点的精确定位
4、 关键点的主方向计算
6、 特征向量
2、多尺度空间极值点检测
尺度空间:目的是检测在尺度变化时仍然稳定的特征;
图像I(x,y)的尺度空间定义:L(x,y,σ)=G(x,y,σ)*I(x,y)
尺度参数σ,当σ 连续变化,G(x,y,σ)构成图像的尺度空间。
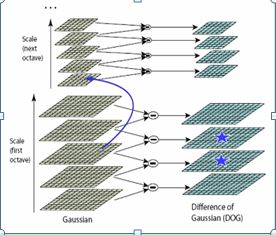
高斯差分尺度空间:为了在尺度空间中检测稳定的关键点,构造高斯差分尺度空间
D(x,y,σ)=[ G(x,y,kσ) - G(x,y,σ) ]* I(x,y) = L(x,y,kσ)- L(x,y,σ)
几个理由:
1) 计算效率高:高斯卷积,减法
2) 高斯差分是对尺度归一化LoG的一个很好的近似, 而尺度归一化的LoG空间具有真正的尺度不变性。
3) 实验比较表明,从尺度归一化LoG空间中提取的图像特征的尺度稳定性最好,优于梯度、Hessian或Harris角点函数。DoG算子是尺度归一化的LoG算子的近似,因此计算比较简单。
(2)将每一组尺度空间中的相邻高斯尺度函数相减,生成高斯差分金字塔:建立成了3维尺度空间形式。
(3)极值点检测:在三维尺度空间中,搜索每个点的26邻域,若该点为局部极值点则保存为候选关键点。
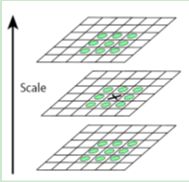
3、关键点的精确定位
由上一步得到的候选关键点,需要进行精确的定位,也就是要确定这个特征点的位置和尺度以及主曲率。
首先,对尺度空间D(x,y,σ)进行二次泰勒展开,再利用二次泰勒展开式进行最小二乘拟合。然后通过计算拟合曲面的极值来进一步确定图像特征点的尺度和图像特征点的位置。
1) 去除低对比度点
将尺度空间函数进行泰勒展开:

对上式求导,并令其为0,得到精确的位置, 得:
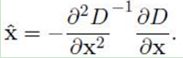
2)在已经检测到的特征点中,要去掉低对比度的特征点和不稳定的边缘响应点。并将其带入到D(x)中,
则保留该特征点,否则丢弃(低对比度候选特征点)。
3)去除边缘处的特征点
由于边缘极值点的抗噪能力差,为了得到稳定的极值点,需要去除边缘的影响。由于每个特征点都有两个主方向,这两个主方向的法曲率分别是曲面在该点法曲率的最大值和最小值。我们用这两个值做比,比值大于设定的阈值时,该极值点被认为在边缘上,否则为非边缘极值点。
主曲率通过Hessian矩阵H求得:
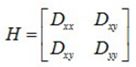
其中:
Dxx=D(x+1,y)+D(x-1,y)-2*D(x,y)
Dyy==D(x,y+1)+D(x,y-1)-2*D(x,y)
Dxy=0.25*[D(x+1,y+1)+D(x+1,y-1)-(D(x-1,y+1)-D(x-1,y-1)]
通过矩阵求解,假设α是H的最大特征值,β是H的最小特征值。则矩阵的迹Tr(H)和矩阵行列式的值Det(H)分别为:Tr(H)= Dxx +Dyy=α+β;Det(H)= Dxx *Dyy - Dxy2=α*β
令α=rβ;
(r + 1)2/r的值在两个特征值相等的时候最小,随着r的增大而增大,因此,为了检测主曲率是否在某域值r下,只需检测:
如果:(α+β)/ αβ>(r+1)2/r,则丢弃。 在Lowe的文章中,取r=10。
4、关键点的主方向计算
上一步中确定了每幅图中的特征点,为每个特征点计算一个方向,依照这个方向做进一步的计算, 利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数,使算子具备旋转不变性。
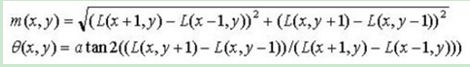
为(x,y)处梯度的模值和方向公式。其中L所用的尺度为每个关键点各自所在的尺度。至此,图像的关键点已经检测完毕,每个关键点有三个信息:位置,所处尺度、方向,由此可以确定一个SIFT特征区域。
梯度直方图的范围是0~360度,其中每10度一个柱,总共36个柱。随着距中心点越远的领域其对直方图的贡献也响应减小.Lowe论文中还提到要使用高斯函数对直方图进行平滑,减少突变的影响。
在实际计算时,我们在以关键点为中心的邻域窗口内采样,并用直方图统计邻域像素的梯度方向。梯度直方图的范围是0~360度,其中每45度一个柱,总共8个柱, 或者每10度一个柱,总共36个柱。Lowe论文中还提到要使用高斯函数对直方图进行平滑,减少突变的影响。直方图的峰值则代表了该关键点处邻域梯度的主方向,即作为该关键点的方向。(直方图中的峰值就是主方向,其他的达到最大值80%的方向可作为辅助方向)
5、描述子的构造
特征点在确定了位置和尺寸之后,下一步就是根据特征点周围的局部特征计算一个特征描述子,其生成过程如下:
1) 旋转坐标。使坐标轴旋转为特征点方向上,确保旋转不变性。
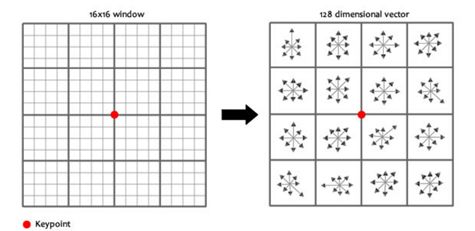
2) 在旋转后的图像上,以特征点为中心取8*8大小的窗口,设特征点位于该窗口的中央位置,特征点周围的方格代表特征点的领域范围,每个小方格代表一个像素,在每个像素上计算梯度。箭头的方向和长度分别表示像素的方向和模值。
3) 将窗口平均分为4*4的子窗口,再利用高斯模糊方法增加与特征点邻近域的权重值、降低特征点较远的权重值,最后计算每个区域的0°、45°、90°、135°、180°、225°、270°、315°方向的梯度累加值,便可以得到特征描述子的特征向量。这时的SIFT特征向量已经取出来对旋转和尺度变化带来的影响。最后进行灰度值的归一化,消除光线的影响。
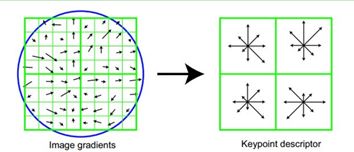
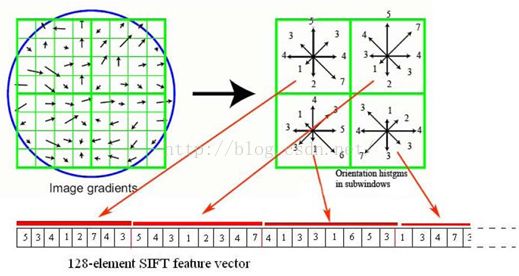
(图左部分的中央为当前关键点的位置,每个小格代表关键点邻域所在尺度空间的一个像素,利用公式求得每个像素的梯度幅值与梯度方向,箭头方向代表该像素的梯度方向,箭头长度代表梯度模值,然后用高斯窗口对其进行加权运算。)
图中蓝色的圈代表高斯加权的范围(越靠近关键点的像素梯度方向信息贡献越大)。然后在每4×4的小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,即可形成一个种子点,如图右部分示。此图中一个关键点由2×2共4个种子点组成,每个种子点有8个方向向量信息。这种邻域方向性信息联合的思想增强了算法抗噪声的能力,同时对于含有定位误差的特征匹配也提供了较好的容错性。
计算keypoint周围的16*16的window中每一个像素的梯度,而且使用高斯下降函数降低远离中心的权重。
在每个4*4的1/16象限中,通过加权梯度值加到直方图8个方向区间中的一个,计算出一个梯度方向直方图。这样就可以对每个feature形成一个4*4*8=128维的描述子,每一维都可以表示4*4个格子中一个的scale/orientation. 将这个向量归一化之后,就进一步去除了光照的影响。
当两幅图像的SIFT特征向量生成后,下一步我们采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。
取图像1中的某个关键点,并找出其与图像2中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离少于某个比例阈值,则接受这一对匹配点。降低这个比例阈值,SIFT匹配点数目会减少,但更加稳定。为了排除因为图像遮挡和背景混乱而产生的无匹配关系的关键点,Lowe提出了比较最近邻距离与次近邻距离的方法,距离比率ratio小于某个阈值的认为是正确匹配。因为对于错误匹配,由于特征空间的高维性,相似的距离可能有大量其他的错误匹配,从而它的ratio值比较高。Lowe推荐ratio的阈值为0.8。但作者对大量任意存在尺度、旋转和亮度变化的两幅图片进行匹配,结果表明ratio取值在0. 4~0. 6之间最佳,小于0. 4的很少有匹配点,大于0. 6的则存在大量错误匹配点。(如果这个地方你要改进,最好给出一个匹配率和ration之间的关系图,这样才有说服力)作者建议ratio的取值原则如下:
ratio=0. 4 对于准确度要求高的匹配;
ratio=0. 6 对于匹配点数目要求比较多的匹配;
ratio=0. 5 一般情况下。
也可按如下原则:当最近邻距离<200时ratio=0. 6,反之ratio=0. 4。ratio的取值策略能排分错误匹配点。
参考的资料链接:
[1] http://blog.csdn.net/abcjennifer/article/details/7639681
[2] http://www.docin.com/p-961006321-f4.html