【计算机视觉——RCNN目标检测系列】二、边界框回归（Bounding-Box Regression）

前言

在上一篇博文：【计算机视觉——RCNN目标检测系列】一、选择性搜索详解我们重点介绍了RCNN和Fast RCNN中一个重要的模块——选择性搜索算法，该算法主要用于获取图像中大量的候选目标框。为了之后更加顺利理解RCNN模型，在这篇博文中我们将主要介绍RCNN及其改进版本——Fast RCNN和Faster RCNN中一个重要模块——边界框回归（Bounding-Box Regression）。

---

一、边界框回归简介

相比传统的图像分类，目标检测不仅要实现目标的分类，而且还要解决目标的定位问题，即获取目标在原始图像中的位置信息。在不管是最初版本的RCNN，还之后的改进版本——Fast RCNN和Faster RCNN都需要利用边界框回归来预测物体的目标检测框。因此掌握边界框回归（Bounding-Box Regression）是极其重要的，这是熟练使用RCNN系列模型的关键一步，也是代码实现中比较重要的一个模块。接下来，我们对边界框回归（Bounding-Box Regression）进行详细介绍。

首先我们对边界框回归的输入数据集进行说明。输入到边界框回归的数据集为${\left\{\left(P^i,G^i\right)\right\}}_{i=1,\cdots ,N}$ ，其中 $P^i=\left(P_x^i,P_y^i,P_w^i,P_h^i\right)$，$G^i=\left(G_x^i,G_y^i,G_w^i,G_h^i\right)$ 。$P^i$ 代表第 $i$个带预测的候选目标检测框即region proposal。 $G^i$是$i$个真实目标检测框即ground-truth。在RCNN和Fast RCNN中， $P^i$ 是利用选择性搜索算法进行获取；Faster RCNN中， $P^i$ 是利用RPN（Region Proposal Network，区域生成网络）获取。在$P^i$ 中，$P_x^i$ 代表候选目标框的中心点在原始图像中的 $x$坐标， $P_y^i$代表候选目标框的中心点在原始图像中的 $y$坐标， $P_w^i$代表候选目标框的长度，$P_h^i$ 代表候选目标框的宽度。 $G^i$的四维特征的含义与 的一样。

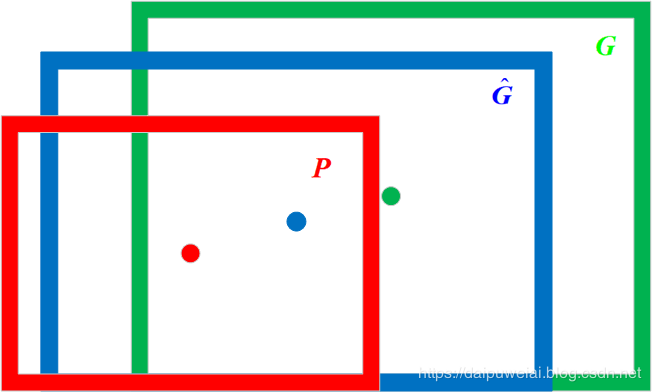
那么边界框回归所要做的就是利用某种映射关系，使得候选目标框（region proposal）的映射目标框无限接近于真实目标框（ground-truth）。将上述原理利用数学符号表示如下：在给定一组候选目标框$P=\left(P_x,P_y,P_w,P_h\right)$ ，寻找到一个映射$f$ ，使得$f\left(P_x,P_y,P_w,P_h\right)=\left({\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h\right)\approx \left(G_x,G_y,G_w,G_h\right)$ 。边界框回归过程图像表示如下图所示。在图1中红色框代表候选目标框，绿色框代表真实目标框，蓝色框代表边界框回归算法预测目标框，红色圆圈代表选候选目标框的中心点，绿色圆圈代表选真实目标框的中心点，蓝色圆圈代表选边界框回归算法预测目标框的中心点。

---

二、边界框回归细节

RCNN论文里指出，边界框回归是利用平移变换和尺度变换来实现映射 。平移变换的计算公式如下：
$$\{\begin{array}{l}{\hat{G}}_x=P_w{d}_x(P)+P_x\\ {\hat{G}}_y=P_h{d}_y(P)+P_y\end{array}\text{\hspace{1em}(1)}$$

尺度变换的计算公式如下：
$$\{\begin{array}{l}{\hat{G}}_w=P_w\exp \left(d_w(P)\right)\\ {\hat{G}}_h=P_h\exp \left(d_w(P)\right)\end{array}\text{\hspace{1em}(2)}$$

其中$d_{\ast }(P)$ ($\ast$ 代表 $x,y,w,h$)，接下来要做的就是求解这4个变换。在边界框回归中，我们利用了线性回归在RCNN论文代表这AlexNet第5个池化层得到的特征即将送入全连接层的输入特征的线型函数。在这里，我们将特征记作 ${\varphi }_5(P)$，那么$d_{\ast }(P)=w_{\ast }^T{\varphi }_5(P)$ 。因此，我们可以利用最小二乘法或者梯度下降算法进行求解 ，RCNN论文中给出了 的求解表达式：
$$w_{\ast }=\underset{{\hat{w}}_{\ast }}{\mathrm{argmin}}\sum _{i=1}^N{\left(t_{\ast }^i-{\hat{w}}_{\ast }^T{\varphi }_5\left(P^i\right)\right)}^2+\lambda {\Vert {\hat{w}}_{\ast }\Vert }^2\text{\hspace{1em}(3)}$$

其中：
$$\{\begin{array}{l}{t}_x=\frac{G_x-P_x}{P_w}\\ t_y=\frac{G_y-P_y}{P_h}\\ t_w=\log \frac{G_w}{P_w}\\ t_x=\log \frac{G_h}{P_h}\end{array}\text{\hspace{1em}(4)}$$

可以看出，上述模型就是一个Ridge回归模型。在RCNN中，边界框回归要设计4个不同的Ridge回归模型分别求解$w_x,w_y,w_w,w_h$。

---

三、相关问题

3.1 为什么使用相对坐标差?

在式(4)中 ，那么为什么要将真实框的中心坐标与候选框的中心坐标的差值分别除以宽高呢？首先我们假设两张尺寸不同，但内容相同的图像，图像如下图所示。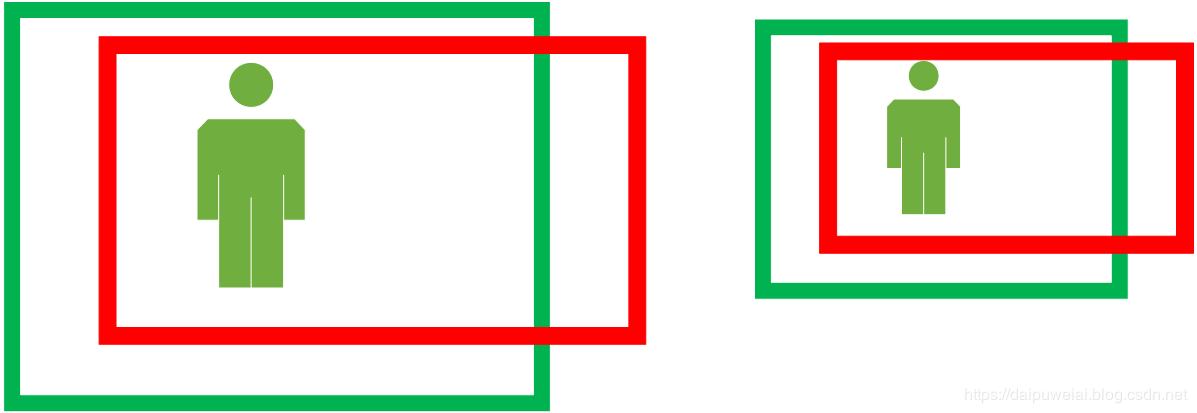
那么我们假设经过CNN提取得到的特征分别为${\varphi }_1$ 和${\varphi }_2$ 。同时，我们假设$x_i$为第$i$个真实目标框的$x$坐标， $p_i$为第$i$个候选目标框的$x$坐标，边界框回归的映射关系为$f$ 。那么我们可以得出：
$$\{\begin{array}{l}f\left({\varphi }_1\right)=x_1-p_1\\ f\left({\varphi }_2\right)=x_2-p_2\end{array}\text{\hspace{1em}(5)}$$

由于CNN具有尺度不变性，因此${\varphi }_1={\varphi }_2$。那么理论上$x_1-p_1=x_2-p_2$。但是观察上图就可明显得出 $x_1-p_1̸=x_2-p_2$，显然由于尺寸的变化，候选目标框和真实目标框坐标之间的偏移量也随着尺寸而成比例缩放，即这个比例值是恒定不变的。

因此，我们必须对$x$坐标的偏移量除以候选目标框的宽， $y$坐标的偏移量除以候选目标框的高。只有这样才能得到候选目标框与真实目标框之间坐标偏移量值的相对值。同时使用相对偏移量的好处可以自由选择输入图像的尺寸，使得模型灵活多变。也就说，对坐标偏移量除以宽高就是在做尺度归一化，即尺寸较大的目标框的坐标偏移量较大，尺寸较小的目标框的坐标偏移量较小。

3.2 为什么宽高比要取对数?

同时在式(4)中$t_w=\log \frac{G_w}{P_w},t_x=\log \frac{G_h}{P_h}$ ，类比问题3.1，我们不禁要问为什么不直接使用宽高的比值作为目标进行学习，非得“多此一举”取对数？结合式(2)可以看出：$t_w=d_w(P),t_h=d_h(P)$ 。也就说式(5)的后两个公式与式(2)可以视为等价。

3.3 为什么IoU较大时边界框回归可视为线性变换？

在这里我们需要回顾下在高等数学中有关等价无穷小的结论：
$$\underset{x\to 0}{\lim }\frac{\log (1+x)}{x}=1\text{\hspace{1em}(6)}$$
也就是说当$x$趋向于0时，我们可有$\log (1+x)\approx x$，即可将$\log (1+x)$ 近似看成线型变换。接下来我们将式(4)的后两个公式进行重写：
$$\{\begin{array}{l}{t}_w=\log \frac{G_w}{P_w}=\log \frac{G_w-P_w+P_w}{P_w}=\log \left(1+\frac{G_w-P_w}{P_w}\right)\\ t_h=\log \frac{G_h}{P_h}=\log \frac{G_h-P_h+P_h}{P_h}=\log \left(1+\frac{G_h-P_h}{P_h}\right)\end{array}\text{\hspace{1em}(7)}$$
也就是说，当$\frac{G_w-P_w}{P_w}$ 和$\frac{G_h-P_h}{P_h}$趋向于0时，即$G_w\approx P_w$和$G_h\approx P_h$时，上式(6)可以近似将对数变换看成线性变换。$G_w\approx P_w$和$G_h\approx P_h$时候选目标框和真实目标框非常接近，即IoU值较大。按照RCNN论文的说法，IoU大于0.6时，边界框回归可视为线型变换。