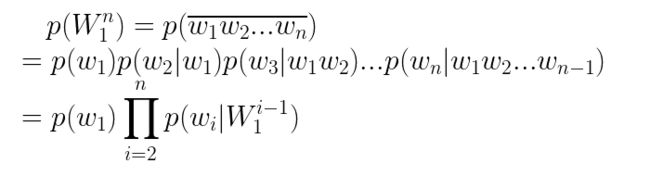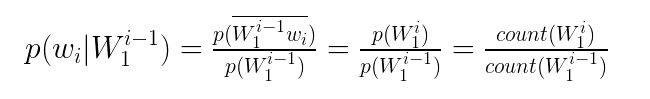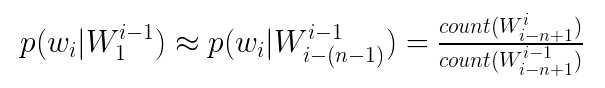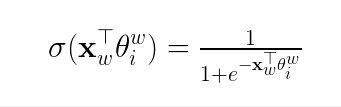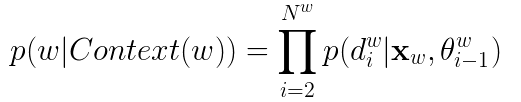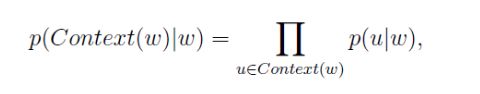自然语言处理（NLP）——词向量

一、Word Embedding概述

简单来说，词嵌入（Word Embedding）或者分布式向量（Distributional Vectors）是将自然语言表示的单词转换为计算机能够理解的向量或矩阵形式的技术。由于要考虑多种因素比如词的语义（同义词近义词）、语料中词之间的关系（上下文）和向量的维度（处理复杂度）等等，我们希望近义词或者表示同类事物的单词之间的距离可以理想地近，只有拿到很理想的单词表示形式，我们才更容易地去做翻译、问答、信息抽取等进一步的工作。
在Word Embedding之前，常用的方法有one-hot、n-gram、但是他们都有各自的缺点，下面会说明。之后，Bengio提出了NLM，是为Word Embedding的想法的雏形，再后来，Mikolov对其进行了优化，即Word2vec，包含了两种类型，Continuous Bag-of-Words Model 和 skip-gram model。

二、Word2vec之前

2.1 one-hot

one-hot是最简单的一种处理方式。通俗地去讲，把语料中的词汇去重取出，按照一定的顺序（字典序、出现顺序等）排列为词汇表，则每一个单词都可以表示为一个长度为N的向量，N为词汇表长度，即单词总数。该向量中，除了该词所在的分量为1，其余均置为0。

2.2 n-gram

n-gram可以表示单词间的位置关系所反映的语义关联，在说明n-gram之前，我们从最初的句子概率进行推导。

假设一个句子S为n个单词有序排列，记为：

                                                                           

我们将其简记为 ，则这个句子的概率为：

                                      

对于单个概率意思为该单词在前面单词给定的情况下出现的概率，我们利用贝叶斯公式可以得到：

                                       

其中最后一项为在语料中出现的频数。但是长句子或者经过去标点处理后的文本可能很长，而且太靠前的词对于词的预测影响不是很大，于是我们利用马尔可夫假设，取该词出现的概率仅依赖于该词前面的n-1个词，这就是n-gram模型的思想。

所以上面的公式变为：

                                        

在这里，我们不对n的确定做算法复杂度上的讨论，详细请参考文献[1]，一般来说，n取3比较合适。此外对于一些概率为0的情况所出现的稀疏数据，采用平滑化处理，此类算法很多，以后有时间再具体展开学习。

2.4 神经语言模型（NLM）

神经语言模型（Neural Language Model）是Word Embeddings的基本思想，

NLM的输入是词向量，词向量和模型参数（最终的语言模型）可以通过神经网络训练一同得到。相比于n-gram通过联合概率考虑词之间的位置关系，NLM则是利用词向量进一步表示词语之间的相似性，比如近义词在相似的上下文里可以替代，或者同类事物的词可以在语料中频数不同的情况下获得相近的概率。结合参考文献[1]，举一个简单例子：

在一个语料C中，S1=“A dog is sitting in the room.”共出现了10000次，S2="A cat is sitting in the room"出现了1次，按照n-gram的模型，当我们输入“A _____ is sitting in the room”来预测下划线上应该填入的词时，dog的概率会远大于cat，这是针对于语料C得到的概率。但是我们希望相似含义的词在目标向量空间中的距离比不相关词的距离更近，比如v(man)-v(woman)约等于v(gentleman)-v(madam)，用这样生成的词向量或者已经训练好的模型在去做翻译、问答等后续工作时，就会很有效果，而NLM利用词向量表示就能达到这样的效果。

NLM的神经网络训练样本同n-gram的取法，取语料中任一词w的前n-1个词作为Context(w)，则（Context(w)，w）就是一个训练样本了。这里的每一个词都被表示为一个长度为L的词向量，然后将Context(w)的n-1个词向量首位连接拼成（n-1）L的长向量。下面为NLM图解：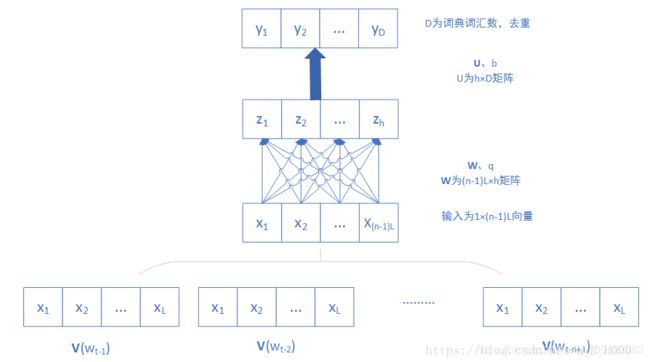

包括四层：输入层、投影层、隐藏层、输出层

注意：这只是取一个词w后输出的向量y，我们需要的就是通过训练集所有的词都做一遍这个过程来优化得到理想的W，q和U，b。

上图中所有参数W、q、U、b，以及词向量都是通过训练得到的。

三、Word2vec

目前学习了解到的Word2vec有基于Hierarchical Softmax和基于Negative Sampling两种方式，由于这两个模型是相反的过程，即CBOW是在给定上下文基础上预测中心词，Skip-gram在有中心词后预测上下文。两个模型都包含三层：输入层、投影层、输出层。

3.1 CBOW

不同于NLM的是，Context(w)的向量不再是前后连接，而是求和，我们记为

3.1.1 基于Hierarchical Softmax

基于Hierarchical Softmax的CBOW所要构建的霍夫曼树所需参数如下：

：从根结点到w对应结点的路径

：路径上包含结点个数

：到w路径上的的结点

：结点编码，根结点不编码

：非叶子结点（包括根结点）对应的向量

霍夫曼树构建按照频数大小有左右两种，其实都是自己约定的，在这里就不麻烦了，构建后左结点编码为0，为正类，右结点为1，为负类。

根据逻辑回归，一个结点被分为正类的概率为

                                                                                 

所以之前我们要构造的目标函数就可以写为以下形式：

对以上式子进行最优化得到Θ和词向量V，我们发现词向量在这里是累加的，我们省略求各个词的V。

3.1.2基于Negative Sampling

对于大规模语料，构建霍夫曼树的工作量是巨大的，而且叶子节点为N的霍夫曼数需要新添(N-1)个结点，而随着树的深度增加，参数计算的量也会增加很多很多，得到的词向量也会不够好，为此，Mikolov作出了优化，将构建霍夫曼树改为随机负采样方法。

对于给定的上下文Context(w)去预测w，如果从语料中就是存在（Context(w),w），那么w就是正样本，其他词就是负样本。

我们设负样本集为，词的标签：

训练目标为增大正样本的概率，减小负样本的概率。可见，对于单词w，基于Hierarchical Softmax将其频数用来构建霍夫曼树，正负样本标签取自结点左右编码；而基于Negative Sampling将其频数作为随机采样线段的子长度，正负样本标签取自从语料中随机取出的词是否为目标词，构造复杂度小于前者。

3.2 Skip-gram

由于Skip-gram是CBOW的相反操作，输入输出稍有不同，推导大同小异。

..................