学习OpenCV-摄像机模型与标定

图像的采集是视觉的开端。针孔摄像机模型是图像采集的一种简单模型，模型中只有进入微型小孔中的光线被采集，其余光线全部被阻拦。该模型数学性质较为理想，但针孔不能为快速曝光采集足够的光线，一般相机采用了透镜模型来增加进光量。透镜的使用不仅背离了简单的几何模型，而且引入了畸变，由此需要利用摄像机标定来使用数学方式纠正主要的偏差。同时，摄像机标定也是将摄像机的自然单位与现实单位联系的重要方法。

摄像机模型

针孔摄像机模型

针孔摄像机模型是最简单的摄像机模型。该模型中光线从场景的某一点发射，通过针孔到达图像平面(投影平面, projective plane)被“切片”。因此，与物体大小相关的图像大小只用焦距(focal length)这一摄像机参数描述。f表示焦距，Z表示摄像机到物体距离，X表示物体长度，x表示图像平面上的物体图像，则可用相似三角形 -x/f = X/Z 得到数值关系。

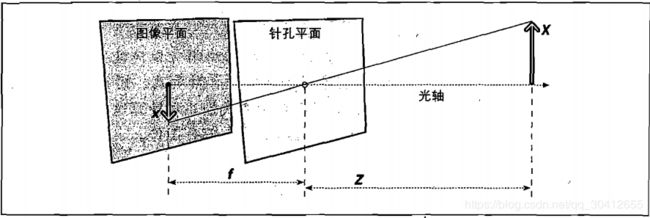
调整的针孔摄像机模型

将针孔摄像机模型中的成像平面与针孔位置交换，即可得到调整后的针孔摄像机模型。针孔被理解为投影中心(center of projection),光线从场景中的某点出发到达针孔，在新的成像平面上被“切片”。由于图像不再是倒立的，数值关系变为 x/f = X/Z 。
光轴与成像平面的交点称为主点。需要注意到成像仪中心不一定在光轴(主点)上，由此需要引入偏移量完成投影。投影方式为
x_screen=f_x(X/Z)+c_x
y_screen=f_y(Y/Z)+c_y
需要注意的是，其中使用了两个不同的焦距。这是因为像素点常常不是正方形的而是矩形的。其中 f_x、f_y 是物理焦距 F 与像素长 s_x 、宽 s_y 的乘积。在摄像机标定中，F、s_x、s_y均不能直接得出，只能得到混合量 f_x、f_y 。

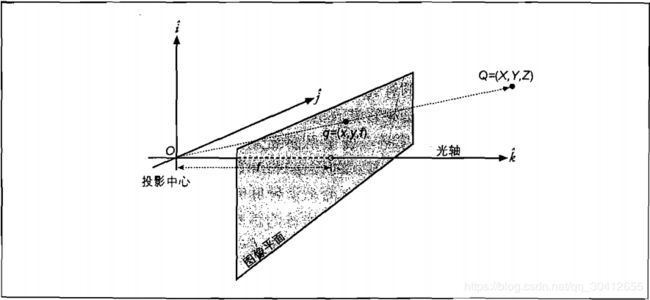
基本投影几何

将坐标为(X,Y,Z)的点映射到到投影平面(x,y)的过程称为投影变换(projective transform)。在这种变换中，可以使用齐次变换方便地完成。通过这种形式，可以将摄像机参数重新排列为一个3×3矩阵(内参数矩阵,camera intrinsics matrix)，得到变换形式为

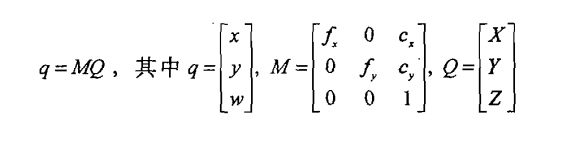
展开可发现 w = Z，且q为其次坐标形式，除以w即可恢复定义形式。

透镜畸变

为了增大进光量、快速生成图像，相机常使用透镜。虽然可以定义不引入任何畸变的透镜，但现实中没有完美的透镜，而且从机械方面也很难让透镜和成像仪保持平行。透镜的主要畸变形式为来自透镜形状的径向畸变和来自机械组装的切向畸变。

径向畸变

源于“筒形”或“鱼眼”影响，在廉价摄像机中显著，而高端摄像机做了很多消除径向畸变的工作，径向畸变不显著。对于径向畸变，成像仪中心畸变为0，随着向边缘移动，越来越严重。实际中，这种畸变较小，且可以用 r=0 周围的泰勒级数前几项定量描述。为了对称，仅使用偶数项，通常采用前两项，对鱼眼镜头，使用三项，分别记为 k₁，k₂，k₃ 。得到以下投影式
x_corrected=x(1+k₁r²+k₂r⁴+k₃r⁶)
y_corrected=y(1+k₁r²+k₂r⁴+k₃r⁶)
其中corrected为校正后的位置，x/y为成像仪上的位置。

切向畸变

源于透镜本身与成像平面本身的不平行。可使用额外参数 p₁,p₂来描述
x_corrected=x+[2p₁y+p₂(r²+2x²)]
y_corrected=y+[p₁(r²+2y²)+2p₂x]

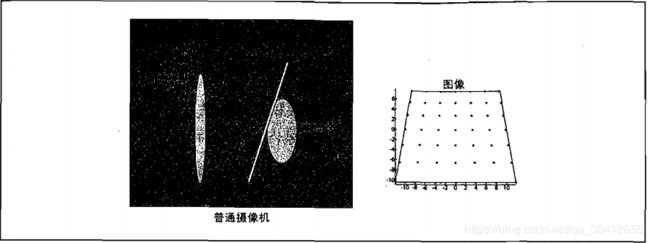
标定

通过标定，可以得到摄像机的内参数矩阵和畸变向量。在OpenCV中，标定是通过对具有独立可标识点的物体进行旋转和移动获得不同角度的图像，从而计算摄像机的相对位置、方向及内参数。

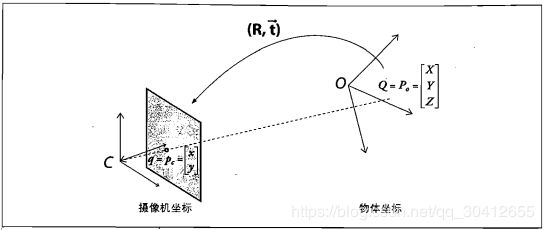
旋转矩阵与平移向量

对物体的图像，可以通过旋转和平移矩阵转换到摄像机坐标。

对于三维旋转，可以通过依次绕 x,y,z 轴旋转来表示。而每个二维旋转，可以通过对应矩阵表示。

综上可得到最终旋转矩阵 R = R_zR_yR_x 。其中R_x/y/z为与对应轴旋转角度相关的旋转矩阵。

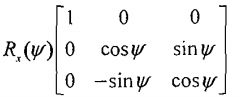
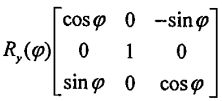
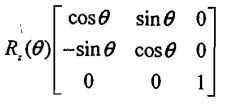
结合平移矩阵，得到物体的点与最终成像点的关系P_c = R(P₀ - T) 。
结合摄像机模型、畸变模型、旋转矩阵的性质及其他约束，使用至少两个视角图像经过计算可得出表示旋转的三个参数、表示位置的三个参数、以及四个摄像机内参数，即完成标定。

棋盘

为了完成标定，需要得到标定物(calibration object)的表征点。原理上说任何合适的表征物都可作标定物，但一般采用棋盘这样的规则模式。棋盘是最常用的标定物(calibration object)。使用中一般使用偶-奇维数的不对称棋盘来唯一确定方向。使用时需要注意使用亚像素角点。

单应性

一个平面到另一个平面的投影映射。

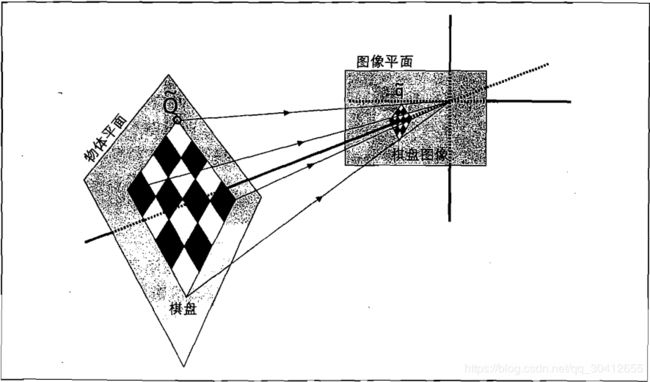
使用齐次坐标表示可以将单应性表示为 q = sHQ 。其中为q为成像的其次坐标[3x1矩阵],s为缩放比例,H包含两部分：用于定位观察的物体平面的物理变换和使用摄像机内参数矩阵的投影，Q为物体坐标的齐次坐标[4x1矩阵]。物理变换由旋转和平移组成，由于采用齐次坐标，可将其组合到矩阵中，得到 W = [ R t ]. 结合摄像机矩阵M,得到 q = sMWQ.考虑到我们只需要物体平面坐标，可以选择定义物体平面使 Z=0，此时将旋转矩阵分解为3个[3x1]向量后可以丢弃其中一个列向量([r₁ r₂ r₃ ] -> [r₁ r₂])。从而 H = M[r₁ r₂ t]。最终 q’ = sHQ’ 。
OpenCV可以利用此公式计算单应性矩阵。其中，利用同一物体的多个图像计算视场的旋转和平移，并计算摄像机的内参数（对不同视场不变）。

摄像机标定

基于求解参数值的要求，需要使用至少2个[3x3]棋盘的两个视场。通常为了标定质量，使用至少10张7x8的棋盘图像。

矫正

使用源图像和摄像机标定得到的畸变参数执行图像重映射，去除图像的畸变效应。在畸变映射不变的情况下，可以先计算畸变映射，然后对每个图像执行重映射而避免了畸变映射的重复计算。