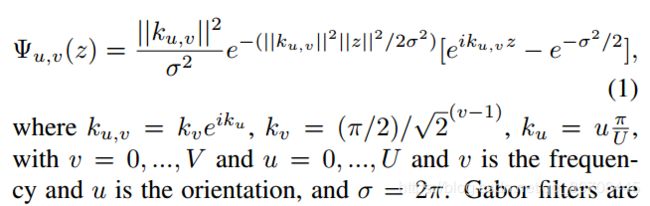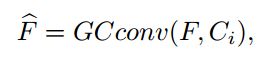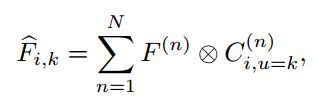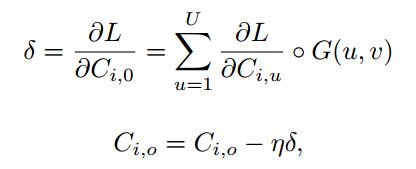论文阅读:Gabor Convolutional Networks
论文:Gabor Convolutional Networks
下载地址:https://arxiv.org/pdf/1705.01450.pdf
摘要
传统滤波器设计具有很好的操作性(参数可调),如Gabor滤波器,其能使得特征具有处理空间变换的能力。然而,在目前流行的深度卷积神经网络(DCNNS)中,这种优良的性能还没有得到很好的研究。本文提出了一种新的深度模型,称为Gabor卷积网络(GCN或Gabor CNN),它将Gabor滤波器引入DCNNS中,以增强深度学习特征对方向和尺度变化的适应性(方向不变性和尺度不变性,因为一般来说深度卷积网络是没有这两个特性的,除非加上很多池化层)。通过将Gabor滤波器替代DCNNS中的卷积算子,形成一种新的方法GCN,并与任何流行的深度学习体系结构兼容。实验结果表明,该算法具有很强的识别目标的能力,尤其在尺度和旋转变化频繁的目标识别中。所提出的GCN具有更少的可学习网络参数,因此更容易使用端到端进行训练。
1引言
引言中介绍了各向异性滤波技术在提取鲁棒的图像特征时的优点,尤其是Gabor滤波器能够保持图像中的频域信息,而且能提取到提取方向依赖于频率的模式内容。而DCNNS虽然能实现端到端的训练,能提取到以数据驱动的鲁棒的特征表示,但是往往需要很大的训练代价和模型复杂度,而且难以对几何变化(方向变化和尺度变化)进行建模,因此对于数据量不够时大的目标和未知的变化难以处理。幸运的是,研究人员已经意识到需要增强模型的转换能力,近年来已经进行了一些尝试。比如采用变形的滤波器(比如空洞卷积),Actively Rotating Filters结合DCNNS能提高网络对旋转的适应能力,但是这些方法都比较复杂,而且对于3D卷积难以实现。此外,从可视化的卷积滤波器来看,这些滤波器存在参数冗余的情况,浅层的滤波器很像Gabor滤波器,如图1所示。众所周知,Gabor滤波器的可控制特性在传统滤波器设计中得到了广泛的应用,因为它增强了信号的尺度和方向分解能力,而DCNNS中大多数卷积滤波器没有这些能力。然而,很少的研究将Gabor滤波器和DCNNS进行结合,有的是利用Gabor滤波器提取图像特征后送入到CNN中,而且是通过Gabor滤波器固定第一或第二个卷积层,这样做主要是为了减少训练CNNs的复杂度。
图1 DCNNs卷积图像和Gabor滤波器模板对比
本文中,我们提出使用传统的手工制作的Gabor滤波器来调节可学习卷积滤波器,以减少可学习网络参数的数量,增强所学特征对方向和尺度变化的鲁棒性。具体地说,在每个卷积层中,卷积滤波器通过具有不同方向和尺度的Gabor滤波器进行调制,以产生卷积Gabor方向滤波器(GoFs),从而使得卷积滤波器在输出特征图中捕捉空间位置、方向选择性和空间频率选择性。GoFs是在CNN的基本元素即卷积滤波器上实现的,因此可以很容易地集成到任何深度的架构中。带有GoF的DCNN,称为GCN,可以学习更健壮的特征表示,特别是对于具有空间转换的图像。此外,由于GoF是基于一组小的可学习卷积滤波器生成的,因此所提出的GCNs模型更紧凑,更易于训练。主要贡献点:(1)首次将Gabor滤波器融合到DCNNs中,从而提高后者针对各种变化的鲁棒性,比如变换,尺度和方向变化;(2)GCNs提高了基于DCNNs架构的性能,获得了最好的结果。
2相关工作
2.1 Gabor滤波器
我们采用了一种不同的方法,通过使用Gabor用于调节所学卷积滤波器的滤波器。具体地说,我们将CNN的基本元素卷积滤波器改为GoFs,以增强Gabor滤波器对每个卷积层的影响。因此,可操纵特性被继承到DCNNS中,以增强特征表示中缩放和方向变化的鲁棒性。
2.2 学习特征表示
考虑到丰富且经常是冗余的卷积滤波器,数据增强被用来实现局部/全局变换不变性。尽管数据扩充的有效性,但其主要缺点在于,学习所有可能的变换通常需要大量的网络参数,这显著增加了训练成本和过度拟合的风险。下面介绍了四种学习特征表示的方法:Spatial Transformer Networks,Oriented Response Networks,Deformable Convolutional network和Scattering Networks,并分别介绍了它们的优缺点。
3 Gabor Convolutional Networks
Gabor卷积网络(GCN)是使用Gabor方向滤波器(GoF)的深卷积神经网络。GoF是一个参数可调的滤波器,通过Gabor滤波器组操纵学习的卷积滤波器来生成增强的特征图。对于GoF,GCN不仅学习的过滤参数显著减少,而且会导致增强的深层模型。
3.1 Convolutional Gabor orientation Filters (GoFs)
Gabor滤波器具有U个方向和V个尺度。为了将可操纵特性合并到GCN中,方向信息被编码到所学的滤波器中,同时尺度信息被嵌入到不同的层中。由于Gabor滤波器在GoF中捕获了方向和尺度信息,增强了相应的卷积特征。
令一个学习的滤波器大小为![]() ,其中
,其中 ![]() 是2D滤波器的尺寸,
是2D滤波器的尺寸,![]() 是Gabor滤波器的方向数。因此一个GoF对应给定尺度下U个Gabor滤波器,而尺度为
是Gabor滤波器的方向数。因此一个GoF对应给定尺度下U个Gabor滤波器,而尺度为 ![]() 的滤波器的调制如下:
的滤波器的调制如下:
![]() 是学习的滤波器,
是学习的滤波器,![]() 为点积操作,
为点积操作,![]() 为调制滤波器。GoF则表示为
为调制滤波器。GoF则表示为
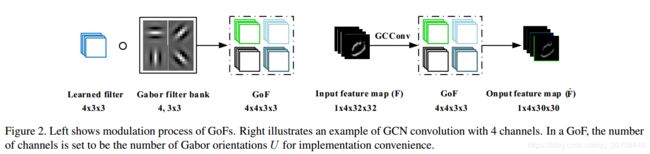
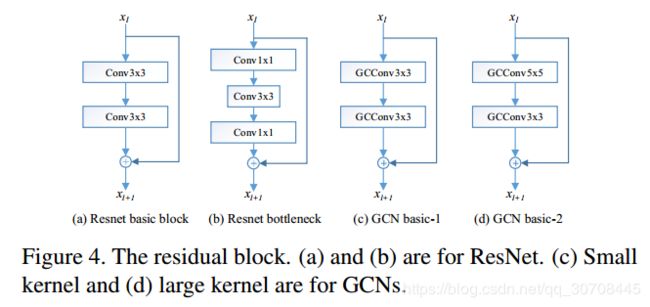
因此,第i 个GoF实际上是 U个3D滤波器,如图2所示
图2 GoFs获得和卷积示意图
在GoFs中,v 随着层数增加而增加,意味着Gabor滤波器的尺度随着层数变化。在每一种尺度下,GoF的尺寸为![]() 。但是,我们只保存
。但是,我们只保存![]() 的可学习滤波器,这样我们就可以通过调制学习到增强性特征,而不会增加参数的数量。
的可学习滤波器,这样我们就可以通过调制学习到增强性特征,而不会增加参数的数量。
3.2 GCN convolution
在GCNs中,GoFs是用来产生特征图的,可以增强深度特征的尺度和方向信息。输出特征图表示如下:
特征图![]() 的通道可以通过下面卷积获得:
的通道可以通过下面卷积获得:
对于图2的理解,左边是得到GoFs的过程,其中可学习的滤波器和Gabor滤波器组进行点积,可以看到尺度为4的四个不同方向的Gabor卷积模板,每个方向分别和可学习的滤波器进行点积,最终获得![]() 的GoF,这个可以看做常规的CNN中的卷积模板,可以看成4个3D卷积滤波器,每个大小为
的GoF,这个可以看做常规的CNN中的卷积模板,可以看成4个3D卷积滤波器,每个大小为 ![]() 。再看右边的那个图,输入特征图为
。再看右边的那个图,输入特征图为![]() ,GoF中的每个 的3D卷积分别和特征图进行卷积操作,每个尺度得到一张增强后的特征图像,最终得到
,GoF中的每个 的3D卷积分别和特征图进行卷积操作,每个尺度得到一张增强后的特征图像,最终得到![]() ,其中卷积的方式采用“Valid”。
,其中卷积的方式采用“Valid”。
3.3 更新GoF的参数
在BP过程中,只需要学习滤波器![]() 中的参数:
中的参数:
4 Implementation and Experiments
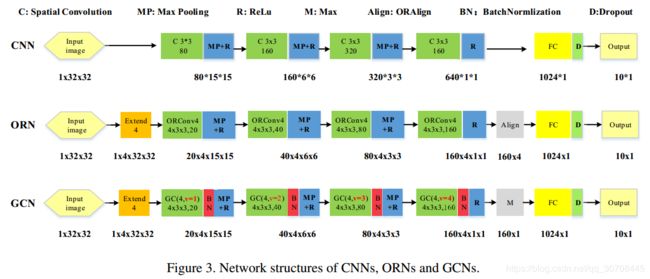
为了评估本文的方法,在Mnist数据集进行实验,并和ORNs方法进行对比。作者还在其他不同的3个数据集上进行实验:SVHN数据集,CIFAR数据集,ImageNet数据集。下面罗列一些实验得到的图表。
4.1 MNIST
一些训练参数这里就不再细说,可以到论文中查看。
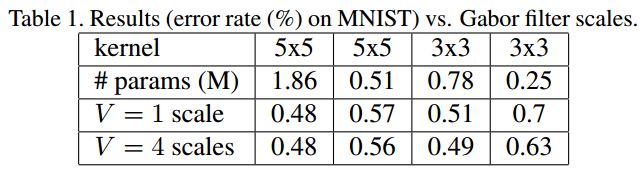
表1可以看到尺度数为4的时候效果比单一尺度更好
表2可以看到在尺度为4时,Gabor滤波器的方向为3到6的时候效果更好
4.2 SVHN
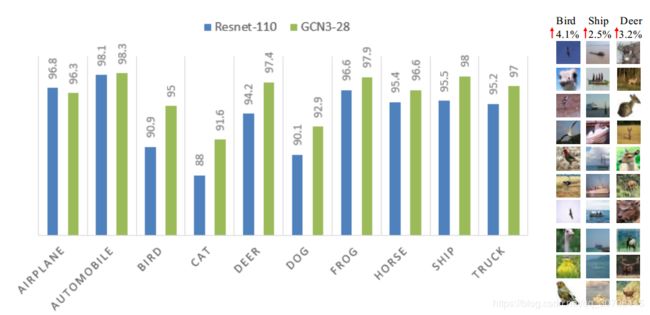
4.3 Natural Image Classification
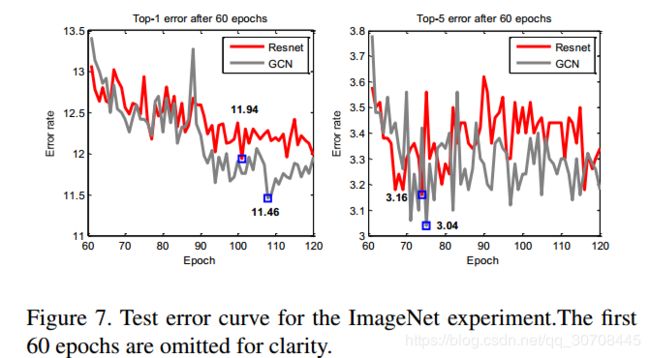
4.4 Large Size Image Classification
5 Conclusion
本文提出了一种新的端到端深度模型,将Gabor滤波器与DCNNS相结合,以增强具有可操纵方向和尺度能力的深度特征表示。所提出的Gabor卷积网络(GCN)通过在DCNNS的基本元素(即卷积滤波器)上引入额外的功能模块,提高了DCNN对旋转和尺度变化的泛化能力。使用流行的体系结构可以很容易地实现GCN。大量的实验表明,GCN显著改善了结果,从而在多个基准上实现了最先进的性能。
Pytorch实现:
https://github.com/bczhangbczhang/Gabor-Convolutional-Networks/tree/pytorch