RNN入门详解及TensorFlow源码实现--深度学习笔记

RNN入门详解及TensorFlow源码实现–深度学习笔记

一、RNN简介

RNNs的目的使用来处理序列数据。在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNNs之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。理论上，RNNs能够对任何长度的序列数据进行处理。但是在实践中，为了降低复杂性往往假设当前的状态只与前面的几个状态相关。

二、循环神经网络原理

1、基本循环神经网络

下图是一个简单的循环神经网络如，它由输入层、一个隐藏层和一个输出层组成：

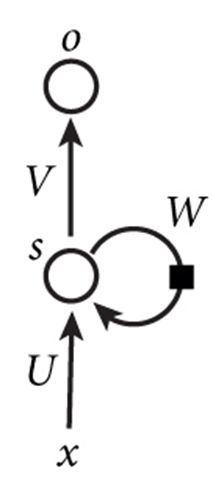
如果把上面有W的那个带箭头的圈去掉，它就变成了最普通的全连接神经网络。x是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）；s是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，你也可以想象这一层其实是多个节点，节点数与向量s的维度相同）；U是输入层到隐藏层的权重矩阵；o也是一个向量，它表示输出层的值；V是隐藏层到输出层的权重矩阵。那么，现在我们来看看W是什么。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。
如果我们把上面的图展开，循环神经网络也可以画成下面这个样子：

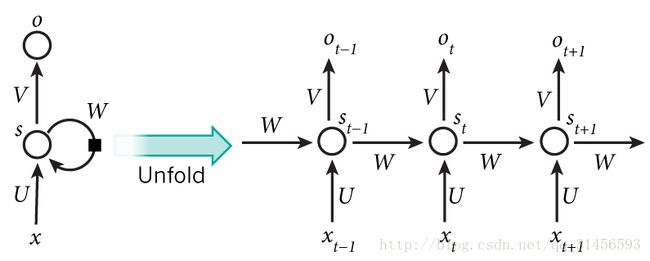
现在看上去就比较清楚了，这个网络在t时刻接收到输入x_t之后，隐藏层的值是s_t，输出值是o_t。关键一点是，s_t的值不仅仅取决于x_t，还取决于o_t。我们可以用下面的公式来表示循环神经网络的计算方法：

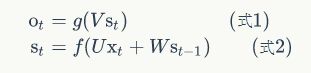
式1是输出层的计算公式，输出层是一个全连接层，也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵，g是激活函数。式2是隐藏层的计算公式，它是循环层。U是输入x的权重矩阵，W是上一次的值s_(t-1)作为这一次的输入的权重矩阵，f是激活函数。
从上面的公式我们可以看出，循环层和全连接层的区别就是循环层多了一个权重矩阵 W。
如果反复把式2带入到式1，我们将得到：

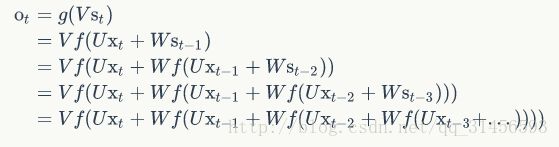
从上面可以看出，循环神经网络的输出值o_t，是受前面历次输入值x_t、x_(t-1)、x_(t-2)、x_(t-3)、…影响的，这就是为什么循环神经网络可以往前看任意多个输入值的原因。

2、循环神经网络的训练算法：BPTT

BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤：

1. 前向计算每个神经元的输出值；

2. 反向计算每个神经元的误差项值，它是误差函数E对神经元j的加权输入的偏导数；

将第 l 层 t 时刻的误差值沿两个方向传播：
• 一个方向是，传递到上一层网络，这部分只和权重矩阵 U 有关；（就相当于把全连接网络旋转90度来看）
• 另一个是方向是，沿时间线传递到初始时刻，这部分只和权重矩阵 W 有关。

3. 计算每个权重的梯度。

最后再用随机梯度下降算法更新权重。

三、语音模型示例

基于 RNN 的语言模型例子
我们要用 RNN 做这样一件事情，每输入一个词，循环神经网络就输出截止到目前为止，下一个最可能的词，如下图所示：

1、把词表达为向量的形式

建立一个包含所有词的词典，每个词在词典里面有一个唯一的编号。
任意一个词都可以用一个N维的one-hot向量来表示。

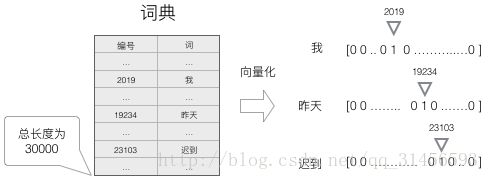
这种向量化方法，我们就得到了一个高维、稀疏的向量，这之后需要使用一些降维方法，将高维的稀疏向量转变为低维的稠密向量。
为了输出 “最可能” 的词，所以需要计算词典中每个词是当前词的下一个词的概率，再选择概率最大的那一个。
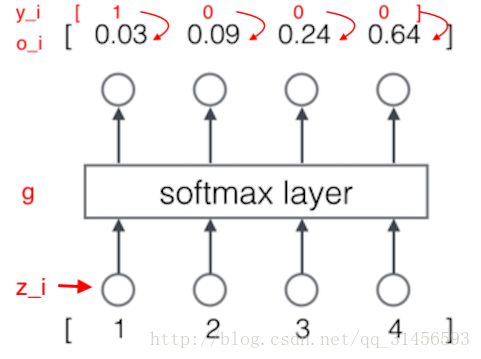
因此，神经网络的输出向量也是一个 N 维向量，向量中的每个元素对应着词典中相应的词是下一个词的概率：

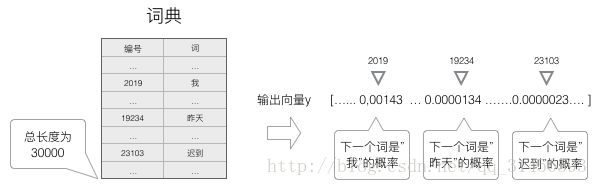
2、采用到 softmax 层作为输出层。

softmax函数的定义：
因为和概率的特征是一样的，所以可以把它们看做是概率。

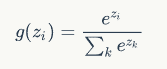
例：

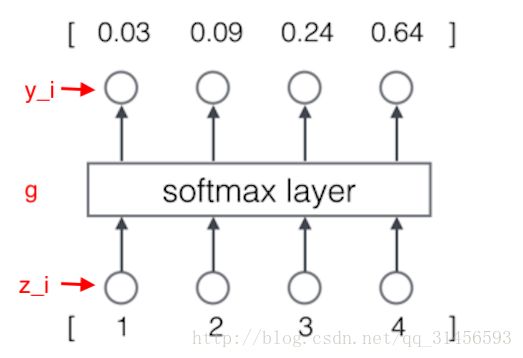
计算过程为：

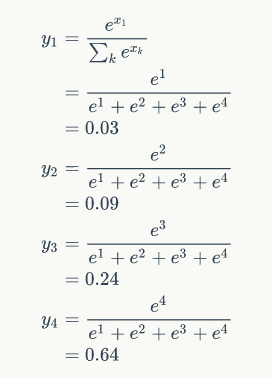
含义就是：
模型预测下一个词是词典中第一个词的概率是 0.03，是词典中第二个词的概率是 0.09。

3、训练

把语料转换成语言模型的训练数据集，即对输入 x 和标签 y 进行向量化，y 也是一个 one-hot 向量

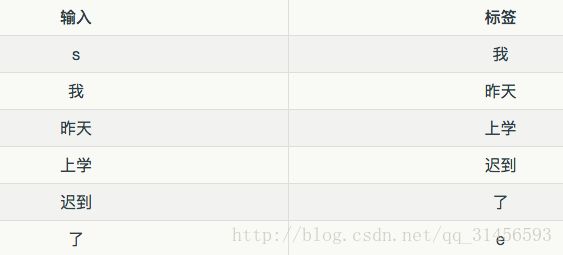
接下来，对概率进行建模，一般用交叉熵误差函数作为优化目标。
交叉熵误差函数，其定义如下：

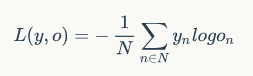
用上面例子就是：

计算过程如下：

有了模型，优化目标，梯度表达式，就可以用梯度下降算法进行训练了

四、各种RNN

1、双向循环神经网络

  Bidirectional RNNs(双向循环神经网络)的改进之处便是，假设当前的输出(第t步的输出)不仅仅与前面的序列有关，并且还与后面的序列有关。例如：预测一个语句中缺失的词语那么就需要根据上下文来进行预测。Bidirectional RNNs是一个相对较简单的RNNs，是由两个RNNs上下叠加在一起组成的。输出由这两个RNNs的隐藏层的状态决定的。如下图所示：

2、深层循环神经网络

  Deep(Bidirectional)RNNs(深层循环神经网络)与Bidirectional RNNs相似，只是对于每一步的输入有多层网络。这样，该网络便有更强大的表达与学习能力，但是复杂性也提高了，同时需要更多的训练数据。Deep(Bidirectional)RNNs的结构如下图所示：

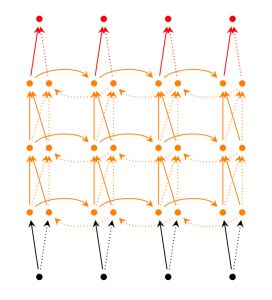
3、GRU

  GRUs也是一般的RNNs的改良版本，主要是从以下两个方面进行改进。一是，序列中不同的位置处的单词(已单词举例)对当前的隐藏层的状态的影响不同，越前面的影响越小，即每个前面状态对当前的影响进行了距离加权，距离越远，权值越小。二是，在产生误差error时，误差可能是由某一个或者几个单词而引发的，所以应当仅仅对对应的单词weight进行更新。GRUs的结构如下图所示。GRUs首先根据当前输入单词向量word vector已经前一个隐藏层的状态hidden state计算出update gate和reset gate。再根据reset gate、当前word vector以及前一个hidden state计算新的记忆单元内容(new memory content)。当reset gate为1的时候，new memory content忽略之前的所有memory content，最终的memory是之前的hidden state与new memory content的结合。

4、LSTM

LSTM 全称叫 Long Short Term Memory networks，它和传统 RNN 唯一的不同就在与其中的神经元（感知机）的构造不同。传统的 RNN 每个神经元和一般神经网络的感知机没啥区别，但在 LSTM 中，每个神经元是一个“记忆细胞”，细胞里面有一个“输入门”（input gate）, 一个“遗忘门”（forget gate）， 一个“输出门”（output gate），俗称“三重门”。

LSTM 的“记忆细胞”

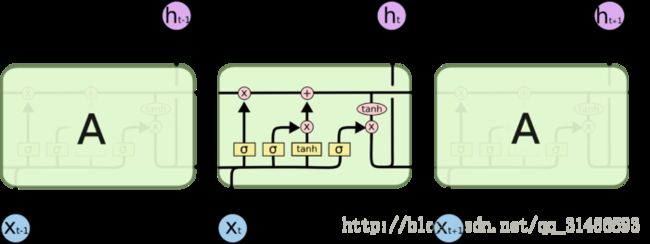
展开来的记忆细胞，上面的黑线是记忆流，下面的黑线是数据流

当前时刻的数据流（包括其他细胞的输入和来自数据的输入）
一条暗线

这个细胞本身的记忆流
两条线互相呼应，互相纠缠，典型的工作流如下：
在“输入门”中，根据当前的数据流来控制接受细胞记忆的影响；接着，在 “遗忘门”里，更新这个细胞的记忆和数据流；然后在“输出门”里产生输出更新后的记忆和数据流。
LSTM 模型的关键之一就在于这个“遗忘门”， 它能够控制训练时候梯度在这里的收敛性（从而避免了 RNN 中的梯度 vanishing/exploding 问题），同时也能够保持长期的记忆性。
目前 LSTM 模型在实践中取得了非常好的效果， 只需要训练一个两三层的LSTM, 它就可以
模仿保罗·格雷厄姆进行写作
生成维基百科的 markdown 页面
帮你写代码

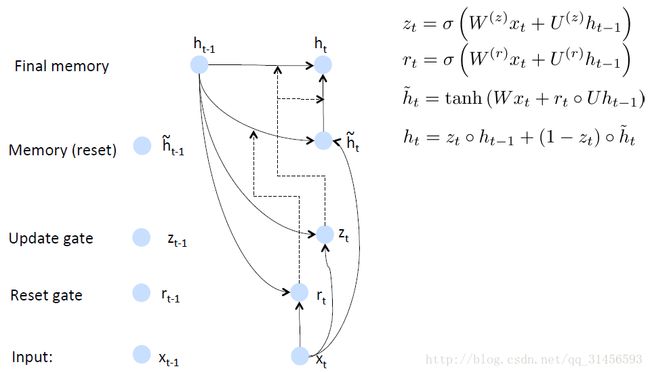
5、LSTMs与GRUs的区别

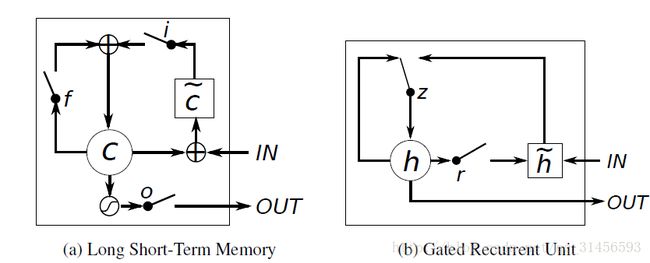
  从上图可以看出，它们之间非常相像，不同在于：
new memory的计算方法都是根据之前的state及input进行计算，但是GRUs中有一个reset gate控制之前state的进入量，而在LSTMs里没有这个gate；
产生新的state的方式不同，LSTMs有两个不同的gate，分别是forget gate (f gate)和input gate(i gate)，而GRUs只有一个update gate(z gate)；
LSTMs对新产生的state又一个output gate(o gate)可以调节大小，而GRUs直接输出无任何调节。

五、RNN的tensorflow源码实现

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
tf.set_random_seed(1)

mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

# hyperparameters
lr = 0.001
training_iters = 100000
batch_size = 128

n_inputs = 28  # shape 28*28
n_steps = 28  # time steps
n_hidden_unis = 128  # neurons in hidden layer
n_classes = 10  # classes 0-9

# tf Graph input
x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_classes])

# Define weights
weights = {
    # (28,128)
    'in': tf.Variable(tf.random_normal([n_inputs, n_hidden_unis])),
    # (128,10)
    'out': tf.Variable(tf.random_normal([n_hidden_unis, n_classes]))
}
biases = {
    # (128,)
    'in': tf.Variable(tf.constant(0.1, shape=[n_hidden_unis, ])),
    # (10,)
    'out': tf.Variable(tf.constant(0.1, shape=[n_classes, ]))
}


def RNN(X, weights, biases):

    # hidden layer for input to cell
    # X(128 batch, 28 steps, 28 inputs) => (128*28, 28)
    X = tf.reshape(X, [-1, n_inputs])
    # ==>(128 batch * 28 steps, 28 hidden)
    X_in = tf.matmul(X, weights['in'])+biases['in']
    # ==>(128 batch , 28 steps, 28 hidden)
    X_in = tf.reshape(X_in,[-1, n_steps, n_hidden_unis])


    # cell
    lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden_unis, forget_bias=1.0, state_is_tuple=True)
    # lstm cell is divided into two parts(c_state, m_state)
    _init_state = lstm_cell.zero_state(batch_size, dtype=tf.float32)
    outputs, states = tf.nn.dynamic_rnn(lstm_cell, X_in, initial_state=_init_state, time_major=False)


    # hidden layer for output as the final results
    results = tf.matmul(states[1], weights['out']) + biases['out']  # states[1]->m_state states[1]=output[-1]
    # outputs = tf.unstack(tf.transpose(outputs,[1,0,2]))
    # results = tf.matmul(outputs[-1], weights['out']) + biases['out']
    return results


pred = RNN(x, weights, biases)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
train_op = tf.train.AdamOptimizer(lr).minimize(cost)

correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    step = 0
    while step * batch_size < training_iters:
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        batch_xs = batch_xs.reshape([batch_size, n_steps, n_inputs])
        sess.run([train_op], feed_dict={
            x: batch_xs,
            y: batch_ys
        })
        if step % 20 ==0:
            print (sess.run(accuracy, feed_dict={
            x: batch_xs,
            y: batch_ys
        }))
        step += 1

参考文献：
http://blog.csdn.net/heyongluoyao8/article/details/48636251
https://www.15yan.com/story/huxAyyeuYAj/
https://zybuluo.com/hanbingtao/note/541458