Matlab_回归分析_逐步回归
例:
(Hald,1960)Hald 数据是关于水泥生产的数据。某种水泥在凝固时放出的热量 Y(单位:卡/克)与水泥中 4 种化学成品所占的百分比有关:
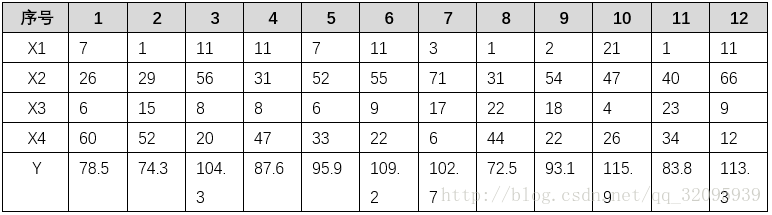
在生产中测得 12 组数据,见表5,试建立 Y 关于这些因子的“最优”回归方程。
对于例 4 中的问题,可以使用多元线性回归、多元多项式回归,但也可以考虑使用逐步回归。从逐步回归的原理来看,逐步回归是以上两种回归方法的结合,可以自动使得方程的因子设置最合理。对于该问题,逐步回归的代码如下:
X=[7,26,6,60;1,29,15,52;11,56,8,20;11,31,8,47;7,52,6,33;11,55,9,22;3,71,17,6;1,31,22,44;2,54,18,22;21,47,4,26;1,40,23,34;11,66,9,12]; %自变量数据
Y=[78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3]; %因变量数据
stepwise(X,Y,[1,2,3,4],0.05,0.10)
% in=[1,2,3,4]表示X1、X2、X3、X4均保留在模型中注:这里的stepwise函数表示逐步回归,第一个参数为自变量数据矩阵,第二个参数为因变量数据,第三个参数表示哪几个向量应该在最初的模型中,第四个参数为Max P-value,不设置时默认为0.05,第个参数为Min P-value,不设置时默认为0.10。正常使用直接使用默认值。
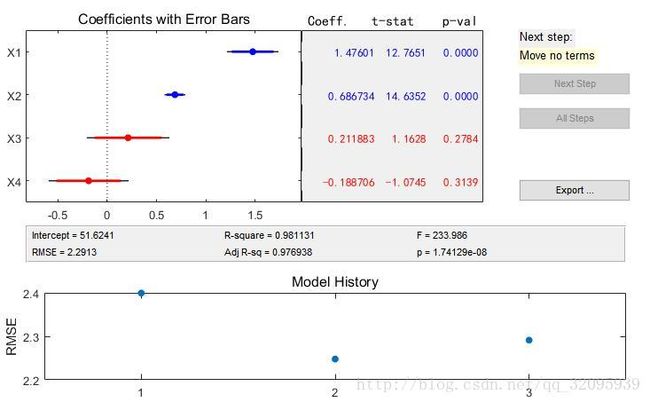
程序运行后一直点Next Step,直到变灰为止。得到最终运行结果后,查看R-square值和p值,前者越接近1,后者越接近0,模型越准。
最后的回归方程为:
Y=51.6241+1.47601*X1+0.686734*X2