动态规划——0-1背包问题
动态规划比较适合用来求解最优问题,比如求最大值、最小值等等。它可以非常显著地降低时间复杂度,提高代码的执行效率。
1、0-1背包问题,回溯求解
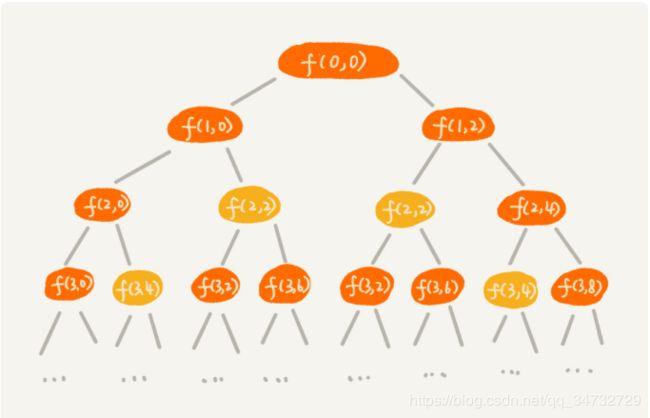
假设背包中有5个物品,重量分别是:2,2,4,6,3。先构建一个递归树,理解回溯算法。function(第i个物品,当前包的重量)
#define maxWeight 9
// 0-1背包问题,回溯求解
// i-索引,从0开始。 cw-当前重量。bag-背包数组。 num-物品个数。 weightInBag-当前放入包中的重量
void huisu(int i, int cw, int *bag, int num, int &weightInBag)
{
if(cw == maxWeight || i == num) // 重量达到上限,或者扫描完所有物品
{
if (cw > weightInBag)
{
weightInBag = cw;
}
return;
}
huisu(i+1, cw, bag, num, weightInBag); // 不放入第i个物品
if (cw + bag[i+1] <= maxWeight) // 满足条件时,放入第i个物品
{
huisu(i+1, cw+bag[i+1], bag, num, weightInBag);
}
}
int main()
{
int weightInBag = 0;
int weight[5] = {2,2,4,6,3};
int num = 5;
huisu(0, 0, weight, num, weightInBag);
cout << "最终包中物品的重量:" <2、优化回溯算法
从上图可以看出,浅色部分,是重复的,可以砍掉重复的分支。此时额外添加一个memary的二维数组,用于记录已经求过的重量,避免重复计算,提高效率。
#define maxWeight 9
bool memary[5][10] = {0}; // 缓存计算过的物品
void huisu_2(int i, int cw, int *bag, int num, int &weightInBag)
{
if (cw == maxWeight || i == num) // 重量达到背包的最大值,或者扫描完最后一个物品
{
if (cw > weightInBag)
{
weightInBag = cw;
}
return;
}
if (memary[i][cw]) // 判断此状态是否数过
{
return;
}
memary[i][cw] = true; // 没有数过的状态,则计为true
huisu_2(i+1, cw, bag, num, weightInBag); // 不装入第i个物品
if (cw + bag[i] <= maxWeight) // 判断是否满足条件
{
huisu_2(i+1, cw+bag[i], bag, num, weightInBag); // 选择装入第i个物品
}
}
int main()
{
int weightInBag = 0;
int weight[5] = {2,2,4,6,3};
int num = 5;
huisu_2(0, 0, weight, num, weightInBag);
system("pause");
return 0;
}这种解决方法,实际上,跟动态规划的执行效率基本上没差别。个人认为,递归深度还有有影响的。
3、动态规划_1
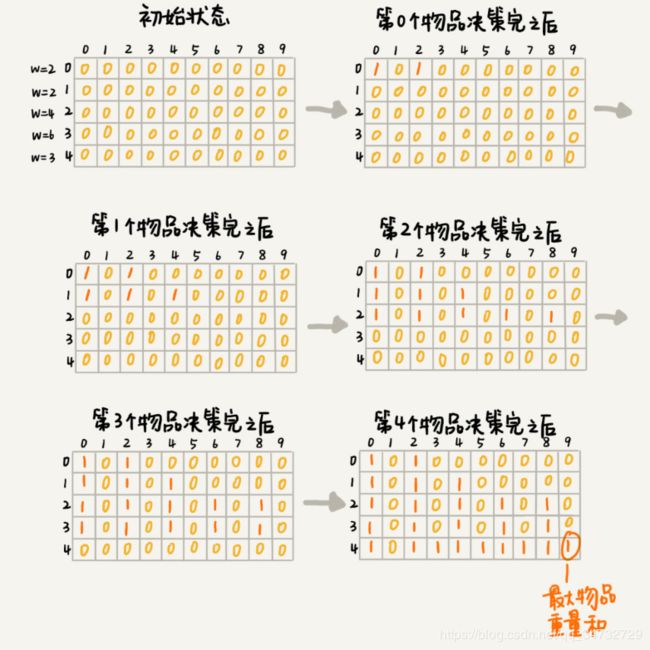
首先把求解过程分为n个阶段,每个阶段决定一个物品是否会放入背包中。同样是递归树,但动态规划,会把重复的状态(结点)合并,只记录不同的状态。然后基于上一层的状态,再推导下一层。这样就保证了每层都不会有重复的,且整个树不会指数增长。
用一个二维数组 states[n][w+1],来记录每层可以达到的不同状态。行标 i,表示第i个物品;列标 j, 表示当前背包的重量。
代码如下:
#define N 5 // 5个物品
#define maxWeight 9
// i 表示行,j 表示列,bag 表示物品包
int dynamic_1(int *bag)
{
bool states[N][maxWeight+1] = {0}; //初始化状态
states[0][0] = true; // 第一个物品不放
if (bag[0] <= maxWeight) // 第一个物品满足条件,放进包里
{
states[0][bag[0]] = true;
}
for (int i = 1; i < N; ++i) // 从第二个物品开始
{
for (int j = 0; j <= maxWeight; ++j) // 不把第i个物品放入背包
{
if (states[i-1][j] == true) // 仅把上一行的状态复制下来
{
states[i][j] = true;
}
}
// 注意: j <= maxWeight - bag[i];
for (int j = 0; j <= maxWeight-bag[i]; ++j) // 满足条件的前提下,把第i个物品放入背包
{
if (states[i-1][j] == true)
{
states[i][j+bag[i]] = true;
}
}
}
// 扫描states最后一行,倒着找到第一个为true的列标,返回,j 即为最大重量。
for (int j = maxWeight; j >= 0; --j)
{
if (states[N-1][j] == true)
{
return j;
}
}
return 0;
}
int main()
{
int weightInBag = 0;
int weight[5] = {2,2,4,6,3};
weightInBag = dynamic_1(weight);
cout << "最终包中物品的重量:" <回溯算法,解题时间复杂度为O(2^n)。动态规划的解题复杂度O(n*w),即物品个数和背包所能承受的重量。但动态规划的空间占用比较大,可以说是空间换时间。
4、动态规划之空间优化
在动态规划过程中,每次装下一个物品时,由彩图可以看出,上一行直接先复制下来(即不添加下一个物品),然后再添加下一个物品。其实可以用一维数组解决这个问题,减少空间。
#define N 5
#define maxWeight 9
// i 第几个物品,从0开始。j 表示列
int dynamic_2(int *bag)
{
bool states[maxWeight + 1] = {0}; // 默认状态都是false
states[0] = true; // 不放第一个物品
if (bag[0] <= maxWeight) // 放第一个物品
{
states[bag[0]] = true;
}
for (int i = 1; i < N; ++i) // 此处的i不再理解为行,可以认为是将要处理的第i个物品
{
// 此处注意,放物品时,是倒着放的。如果正向放,会影响后面的数据。
for (int j = maxWeight - bag[i]; j >= 0; --j) // 把第i个物品放入背包,保证放入物品后,不超重。
{
if (states[j] == true)
{
states[j + bag[i]] = true;
}
}
}
// 倒着扫描,找到最大值,输出。
for (int j = maxWeight; j >= 0; --j)
{
if (states[j] == true)
{
return j;
}
}
return 0;
}
int main()
{
int weightInBag = 0;
int weight[5] = {2,2,4,6,3};
weightInBag = dynamic_2(weight);
cout << "最终包中物品的重量:" <特别强调一下代码中的第14行,j 需要从大到小来处理。如果我们按照 j 从小到大处理的话,会出现 for 循环重复计算的问题。
5、0-1背包升级版——添加物品价值
物品价值为:3,4,8,9,6
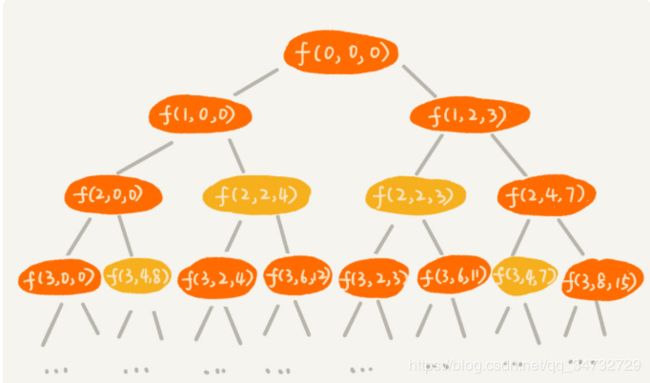
如下递归树所示,每个节点有三个变量,function(第i个,当前背包中物品的总重量,当前背包中物品的总价值)。
对于浅颜色的节点,物品重量一样,但是价值不同,此时需要保留价值较大的节点,砍掉价值小的节点。下面代码,依然选择states[][]二维数组,来保存状态。只是二维数组中的值不再局限于true or false ,而是具体的价值。
#define N 5
#define maxWeight 9
int dynamic_3(int *bag, int *val)
{
int states[N][maxWeight+1] = {0};
for (int i = 0; i < N; ++i) // 初始化 -1。当物品不放入时,赋值价值为0,放入时,价值发生变化。
{
for(int j = 0; j < maxWeight + 1; ++j)
{
states[i][j] = -1;
}
}
states[0][0] = 0; // 特殊处理第一个物品,不放入时
if (bag[0] <= maxWeight) // 第一个物品放入时
{
states[0][bag[0]] = val[0];
}
for (int i = 1; i < N; ++i)
{
for (int j = 0; j <= maxWeight; ++j) // 不放入第i个物品,直接将上面的赋值给下一行
{
if (states[i-1][j] >= 0)
{
states[i][j] = states[i-1][j];
}
}
for (int j = 0; j <= maxWeight - bag[i]; ++j) // 放入第i个物品,且先进行判断
{
if (states[i-1][j] >= 0)
{
int v = states[i-1][j] + val[i]; // 判断加上val值,是否比已有的值大。
if (v > states[i][j+bag[i]]) // 选择较大的val值
{
states[i][j + bag[i]] = v; // 大于已有值,则替换。
}
}
}
}
int maxVal = -1;
for (int j = 0; j <= maxWeight; ++j) // 由于最后一行不确定哪个值最大,所以需要全部扫描
{
if (states[N - 1][j] > maxVal)
{
maxVal = states[N-1][j];
}
}
return maxVal;
}
int main()
{
int weight[5] = {2,2,4,6,3};
int val[5] = {3,4,8,9,6};
valInBag = dynamic_3(weight, val);
cout << "最大价值:" << valInBag << endl;
system("pause");
return 0;
}6、回溯算法——添加物品价值
物品价值为:3,4,8,9,6
#define maxWeight 9
void huisu_3(int i, int cw, int cv, int *bag, int *val, int num, int &weightInBag, int &valInBag)
{
if (cw == maxWeight || i == num)
{
if (cv > valInBag) // 最后不再求最大重量,而是求最大价值
{
valInBag = cv;
weightInBag = cw;
}
return;
}
huisu_3(i+1, cw, cv, bag, val, num, weightInBag, valInBag); // 不加第i个物品
if (cw + bag[i] <= maxWeight) // 满足条件的情况下,添加第i个物品,重量加,价值也加
{
huisu_3(i+1, cw + bag[i], cv + val[i], bag, val, num, weightInBag, valInBag);
}
}
int main()
{
int weightInBag = 0;
int weight[5] = {2,2,4,6,3};
int num = 5;
int val[5] = {3,4,8,9,6};
int valInBag = 0;
huisu_3(0, 0, 0, weight, val, num, weightInBag, valInBag);
cout << "最大价值:" << valInBag << endl;
cout << "最终包中物品的重量:" <