反向传播公式推导

参考：《神经网络与深度学习》
https://legacy.gitbook.com/book/xhhjin/neural-networks-and-deep-learning-zh

该笔记主要是反向传播公式的推导，理解反向传播的话建议看其他博客中更加具体的例子或者吴恩达老师反向传播介绍的视频（有具体数字的例子），主要有4个公式的推导：
$${\delta }_j^L=\frac{\partial C}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L}\cdot {\sigma }^{\prime }(z_j^L)\text{\hspace{1em}(BP1)}$$

$${\delta }^l={W^{l+1}}^{\mathsf{T}}\cdot {\delta }^{l+1}\odot {\sigma }^{\prime }(z^l)\text{\hspace{1em}(BP2)}$$

$$\frac{\partial C}{\partial w_{jk}^l}=\frac{\partial C}{\partial z_j^l}\cdot \frac{\partial z_j^l}{\partial w_{jk}^l}={\delta }_j^l\cdot a_k^{l-1}\text{\hspace{1em}(BP3)}$$

$$\frac{\partial C}{\partial b_j^l}=\frac{\partial C}{\partial z_j^l}\cdot \frac{\partial z_j^l}{\partial b_j^l}={\delta }_j^l\text{\hspace{1em}(BP4)}$$

1. 公式BP1的推导：
   先推导神经网络最后一层L的公式，假设一个二分类的神经网络在最后一层如下图所示：
   
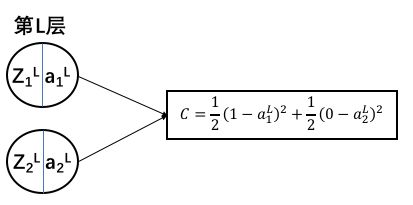
   C表示损失（或者叫loss）
   从公式中可以看出：$\frac{\partial C}{\partial a_j^L}$可直接求出来，接下来是推导$\frac{\partial C}{\partial z_j^L}$, 定义${\delta }_j^L=\frac{\partial C}{\partial z_j^L}$

$${\delta }_j^L=\frac{\partial C}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L}\cdot {\sigma }^{\prime }(z_j^L)\text{\hspace{1em}(1)}$$

写成矩阵的形式：
$${\delta }^L=\frac{\partial C}{\partial a^L}\odot {\sigma }^{\prime }(z^L)={\Delta }_{a}C\odot {\sigma }^{\prime }(z^L)\text{\hspace{1em}(2)}$$
公式中$\odot$表示Hadamard积。

2. 公式BP2的推导
   L层已经能计算了，接下来是推导前一层的情况，为了表示方便，直接考虑从l+1层到l层的情况，神经网络以及变量命名示意图如下图所示：
   
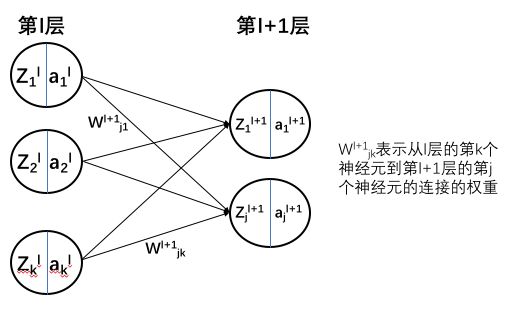
   （这里$w_{jk}^{l+1}$表示从k神经元到j神经元，理解起来有些拗口，主要是为了方便正向传播中W矩阵的表示，也可以按照自己喜好来进行变量命名，反向传播公式推导麻烦很大程度上是因为变量命令麻烦。）
   先得弄清楚前向传播中的一个公式：
   $$z_j^{l+1}=\sum _{k=1}^k{w}_{jk}^{l+1}\cdot a_k^l+b_j^{l+1}\text{\hspace{1em}(3)}$$

写成矩阵形式为：
$$Z^{l+1}=W^{l+1}\cdot A^l+B^{l+1}\text{\hspace{1em}(4)}$$
在公式（3）中，现在$\frac{\partial C}{\partial z_j^{l+1}}$已知，需要求$\frac{\partial C}{\partial a_k^l}$,自然想到链式求导法则：
$$\frac{\partial C}{\partial a_k^l}=\sum _{j=1}^j\frac{\partial C}{\partial z_j^{l+1}}\cdot \frac{\partial z_j^{l+1}}{\partial a_k^l}\text{\hspace{1em}(5)}$$

也可以从物理意义去理解这个公式，$\frac{\partial C}{\partial a_k^l}$表示$a_k^l$的变化对C的影响大小，$a_k^l$可以从$z_j^{l+1}(j=1...J)$来影响C的大小，所以公式（5）中需要有累加。
公式（5）继续化简，这里需要参考公式（3）：
$$\frac{\partial C}{\partial a_k^l}=\sum _{j=1}^j{\delta }_j^{l+1}\cdot \frac{\partial z_j^{l+1}}{\partial a_k^l}=\sum _{j=1}^j{\delta }_j^{l+1}\cdot w_{jk}^{l+1}\text{\hspace{1em}(6)}$$

$$\frac{\partial C}{\partial z_k^l}=(\sum _{j=1}^j{\delta }_j^{l+1}\cdot w_{jk}^{l+1})\cdot {\sigma }^{\prime }(z_k^l)\text{\hspace{1em}(7)}$$

写成矩阵形式有：
$$\left[\begin{array}{c}\frac{\partial C}{\partial z_1^l}\\ \frac{\partial C}{\partial z_2^l}\\ \frac{\partial C}{\partial z_k^l}\end{array}\right]=\left[\begin{array}{ccc}{w}_{11}^{l+1}& w_{21}^{l+1}& w_{j1}^{l+1}\\ w_{12}^{l+1}& w_{22}^{l+1}& w_{j2}^{l+1}\\ w_{1k}^{l+1}& w_{2k}^{l+1}& w_{jk}^{l+1}\end{array}\right]\cdot \left[\begin{array}{c}{\delta }_1^{l+1}\\ {\delta }_2^{l+1}\\ {\delta }_j^{l+1}\end{array}\right]\odot \left[\begin{array}{c}{\sigma }^{\prime }(z_1^l)\\ {\sigma }^{\prime }(z_2^l)\\ {\sigma }^{\prime }(z_k^l)\end{array}\right]\text{\hspace{1em}(8)}$$

$$\left[\begin{array}{c}\frac{\partial C}{\partial z_1^l}\\ \frac{\partial C}{\partial z_2^l}\\ \frac{\partial C}{\partial z_k^l}\end{array}\right]={\left[\begin{array}{ccc}{w}_{11}^{l+1}& w_{12}^{l+1}& w_{1k}^{l+1}\\ w_{21}^{l+1}& w_{22}^{l+1}& w_{2k}^{l+1}\\ w_{j1}^{l+1}& w_{j2}^{l+1}& w_{jk}^{l+1}\end{array}\right]}^{\mathsf{T}}\cdot \left[\begin{array}{c}{\delta }_1^{l+1}\\ {\delta }_2^{l+1}\\ {\delta }_j^{l+1}\end{array}\right]\odot \left[\begin{array}{c}{\sigma }^{\prime }(z_1^l)\\ {\sigma }^{\prime }(z_2^l)\\ {\sigma }^{\prime }(z_k^l)\end{array}\right]\text{\hspace{1em}(9)}$$

$${\delta }^l={W^{l+1}}^{\mathsf{T}}\cdot {\delta }^{l+1}\odot {\sigma }^{\prime }(z^l)\text{\hspace{1em}(10)}$$

3.公式BP3的推导：
然后推导$\frac{\partial C}{\partial w_{jk}^l}$ 和 $\frac{\partial C}{\partial b^l}$, 这也是神经网络中实际参数更新需要计算的参数，先推导$\frac{\partial C}{\partial w_{jk}^l}$。
根据公式（3）可知：
$$\frac{\partial C}{\partial w_{jk}^l}=\frac{\partial C}{\partial z_j^l}\cdot \frac{\partial z_j^l}{\partial w_{jk}^l}={\delta }_j^l\cdot a_k^{l-1}\text{\hspace{1em}(11)}$$

4.公式BP4的推导：
然后推导$\frac{\partial C}{\partial b^l}$
$$\frac{\partial C}{\partial b_j^l}=\frac{\partial C}{\partial z_j^l}\cdot \frac{\partial z_j^l}{\partial b_j^l}={\delta }_j^l\text{\hspace{1em}(12)}$$