LIF神经元介绍

Integrate-And-Fire Models

---

基础知识

轴突：动作电位（电位差形成电流）=神经递质发放=脉冲产生
树突或细胞体：神经递质的接受=产生内外膜电位差（电流产生）=接收脉冲
脉冲编码：多采用平均发放率，计算在一段时间内的。
泄露电流（对于与LIF中的L（leaky））：生物概念，膜电压沿轴突传递过程中的损失，在硬件电路中用电阻代替。

概述

神经元动力学可以被设想为一个总和过程(有时也称为“集成”过程)，并结合一种触发动作电位高于临界电压的机制。
一般来所， Vrest V r e s t < Vth V t h ，当 Vi(t) V i ( t ) （对所有所输入求和后的所得到电压）上升到阈值 θ θ 时就会引起动作电位从而产生脉冲。发放的脉冲的形状是相似的，其传递的信息实质在于某时刻脉冲的有无。
动作电位被称为事件（忽视脉冲的形状）的神经元模型被称为IF模型。对于描述IF模型，我们需要两样东西：
1.膜电位 Vi(t) V i ( t ) 的公式
2.产生脉冲的机制

LF模型

硬件模型：IF模型只有一个电容，没有并联的电阻，因为电阻实际等效于泄露电流，对应LIF模型。
dVdt=1CI(t) d V d t = 1 C I ( t )

LIF模型

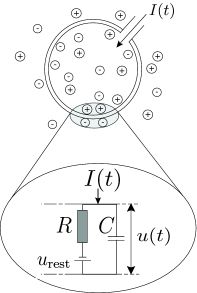
当然我们侧重的并不是IF模型，而是 leaky integrate-and-fire模型（LIF），后者比前者更加接近真实的生物神经元，leaky表示泄露，由于细胞膜是不断进行膜内外离子的交换，所以当只有一次输入时，电压会自动发生泄漏逐渐回落到静息状态。对于LIF模型一般是认为先下降低于 Vrest V r e s t ,再上升的静息电位处，而IF神经元一般是认为直接回落到静息状态处，这里涉及到一个reset电位。这里的reset可以看成输入一个短暂的电流脉冲 Ir=−qr∑fδ(t−t(f))=−C(ϑ−ur)S(t), I r = − q r ∑ f δ ( t − t ( f ) ) = − C ( ϑ − u r ) S ( t ) ,
其中 qr=C(ϑ−ur) q r = C ( ϑ − u r ) 为电容需要移除的电荷量，因为这是模电压直接由电容器的电压设定。

由右图知，由于导数存在无穷情况，会造成梯度问题。所欲不能直接使用。
左图黑色的对应上述的LIF响应，同时LIF的形状与ANNs中的激活函数relu和softplus等激活函数非常相似，relu对于LIF，加入白噪声后得到形状如soft LIF对应softplus

LIF响应公式

r(j) r ( j ) 为firing rate， j j 为膜电压
LIF是真实神经元的简化版，拥有部分缺陷

I(t)=IR+IC I ( t ) = I R + I C

其中 IR=UR/R,UR=U−Urest I R = U R / R , U R = U − U r e s t ,
IC I C 是对电容C（ C=q/u C = q / u q为充电电荷，u是电压）进行充电。
IC=dq/dt=Cdu/dt I C = d q / d t = C d u / d t

得到
I(t)=u(t)−urestR+Cdudt. I ( t ) = u ( t ) − u r e s t R + C d u d t .
再乘R，并引进时间参数 τm=RC τ m = R C （leaky integrator才有的参数）

可以得到标准式：
τmdudt=−[u(t)−urest]+RI(t). τ m d u d t = − [ u ( t ) − u r e s t ] + R I ( t ) .
u为膜电位， τm τ m 为膜时间常数
上式被称为被动膜方程式。

求解上式
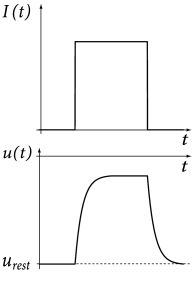
假设t=0时，膜电位为 urest+Δu u r e s t + Δ u ,当t>0时，输入电流 I(t) I ( t ) 衰减到0,可以想象当时间足够长，膜电压肯定会恢复静息状态，所以当以 urest+Δu u r e s t + Δ u 为初始条件，其解 u(t)−urest=Δu exp(−t−t0τm)for t>t0  u ( t ) − u r e s t = Δ u   exp ⁡ ( − t − t 0 τ m ) f o r   t > t 0  
当没有输入，膜电压以指数衰减到静息状态,膜时间常数 τm=RC τ m = R C 表示衰减的时间，对于一个典型的神经元，它的范围是10毫秒，相对于一个峰值的持续时间1毫秒要长

注意：如果有不断的输入，膜电压会逐渐稳定 u(∞)=urest+RI0 u ( ∞ ) = u r e s t + R I 0 ,因为电容C会充满电。

虚线为真实，一般用实线替代， Ur U r 为重置电压

脉冲产生的门槛，首先术语“fire time”是指神经元产生一个动作电位 t(f) t ( f ) 的时间。
在LIF模型中定义为：
t(f):u(t(f))=ϑ. t ( f ) : u ( t ( f ) ) = ϑ .
含义是在某个时刻产生的动作电位，使膜电位达到 Vthre V t h r e
根据上图实线，动作电位产生后马上将膜电位
设置 Vr V r
limδ→0;δ>0u(t(f)+δ)=ur. lim δ → 0 ; δ > 0 u ( t ( f ) + δ ) = u r .

实质上LIF模型就是由两部分组成
1.leaky intergration： τmdudt=−[u(t)−urest]+RI(t). τ m d u d t = − [ u ( t ) − u r e s t ] + R I ( t ) .
2.reset: limδ→0;δ>0u(t(f)+δ)=ur. lim δ → 0 ; δ > 0 u ( t ( f ) + δ ) = u r .

对于神经元i，其发放的脉冲序列可以表示为：
Si(t)=∑fδ(t−t(f)i) S i ( t ) = ∑ f δ ( t − t i ( f ) )
其中 f f 是脉冲的标签， δ(x) δ ( x ) 是Dirac函数，所以脉冲如上图的实线所示。

总电流 I(t)+Ir(t) I ( t ) + I r ( t )
得到任意时刻的电压 u(t)=urest+∑f(ur−ϑ)exp(−t−t(f)τm)+Rτm∫∞0exp(−sτm)I(t−s)ds, u ( t ) = u r e s t + ∑ f ( u r − ϑ ) exp ⁡ ( − t − t ( f ) τ m ) + R τ m ∫ 0 ∞ exp ⁡ ( − s τ m ) I ( t − s ) d s ,
第二个是由于补偿电流输入脉冲引起，第三项由于电容放电
可以改写成： u(t)=∫∞0η(s)S(t−s)ds+∫∞0κ(s)I(t−s)ds. u ( t ) = ∫ 0 ∞ η ( s ) S ( t − s ) d s + ∫ 0 ∞ κ ( s ) I ( t − s ) d s .
引进滤波器 η(s)=(ur−ϑ)exp(−sτm) η ( s ) = ( u r − ϑ ) exp ⁡ ( − s τ m ) 和 κ(s)=1Cexp(−sτm) κ ( s ) = 1 C exp ⁡ ( − s τ m ) 比LIF神经元更具普遍性，因为过滤器不需要是指数函数，但是可以有任意的形状
前一个滤波器描述的是膜电压reset，后者是关于膜电压的线性模型。

---

LIF神经元的缺陷

上面我们说到LIF神经元模型，这模型是高度简化的，同时忽略了很多的有关神经动力学的内容。
1.输入( input i n p u t ),在该模型中输入是突触前神经元或注入电流的线性叠加，并独立于后突触神经元。
2.每次激活后直接reset，不能保留前一脉冲。

适应性
当输入电流时，真实神经元有一个适应的过程，即从当输入一个恒定的电流 I I （从0到K整个过程），根据LIF模型，我们可以推断发放率应该是恒定的，这是因为reset的存在。但在真实神经元并非这样工作，需要经过一个过程才能输出稳定的发放率。

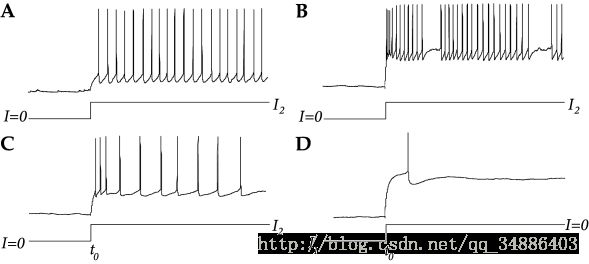
A为快速脉冲神经元（fast-spiking），其本身就没有适应性所以可以很好的对应LIF模型，许多的抑制神经元都是一些快速脉冲神经元，除了 regular-spiking 和fast-spiking还有 bursting and stuttering神经元，当有恒定输入时，会产生一系列脉冲会周期的（bursting）或不周期的（stuttering）因为长间隔而产生中断。如图B
上图，快速脉冲（fast-spiking）神经元(A)在不适应的情况下有短的间隔时间间隔，而常规的脉冲神经元(C)表现适应，可见在间隔期间增加。许多神经元在抑制电流 I1<0 I 1 < 0 被终止后发出抑制反弹尖峰（D）

输入与动作电位相关

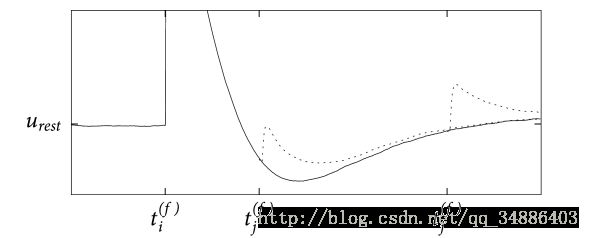
ti t i 到 tj t j 的时间差为绝对不应期，后面的是相对不应期
虚线为两个不同的假设不同的到来时间，虚线为对膜电位的影响情况
我们不能指望它解释神经元的完整生物化学和生物物理学。我们也不期望它解释由树枝状树上的一些“热点”中的有效电流引起的高度非线性相互作用。然而，当涉及到产生尖峰时，即时精确的事件发生时，整合和火力模型是非常准确的。因此，它可能潜在地是神经元中尖峰生成的有效模型，或者更准确地说在神经元中。