图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
一、图的定义
在线性表中,数据元素之间是被串起来的,仅有线性关系,每个数据元素之间只有一个直接前驱和一个直接后继。
在树形结构中,数据元素之间有着明显的层次关系,并且每一层上的数据元素可能和下一层中多个元素相关,但只能和上一层中一个元素相关。
图是一种较线性表和树更加复杂的数据结构。在图形结构中,结点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。
图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
注意:
1.线性表中我们把数据元素叫作元素,树中将数据元素叫结点,在图中数据元素叫顶点。
2.线性表中可以没有数据元素,称为空表。树中可以没有结点,叫做空树。但在图结构中,不允许没有顶点。
3.线性表中,相邻数据元素之间具有线性关系,树结构中,相邻两层的结构具有层次关系。而图中,任意两个顶点之间都有可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
1.1各种图定义
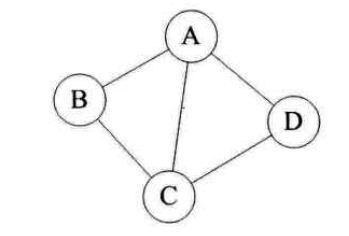
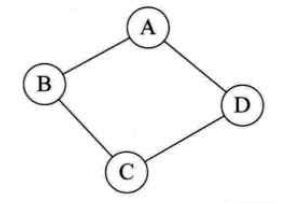
无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边,用无序偶对(Vi,Vj)来表示。如果图中任意两个顶点之间的边都是无向边,则称该图为无向图。如图所示:由于是无方向的,连接顶点A与D的边,可以表示成无序对(A,D),也可以写成(D,A)。
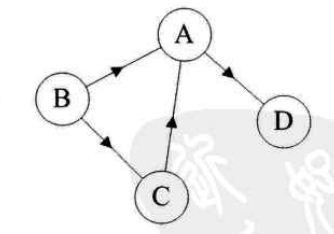
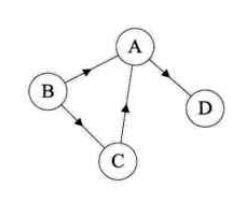
有向边:若从顶点Vi到Vj的边有方向,则称这条边为有向边,也称为弧。用有序偶对
在图中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。如图所示:含有n个顶点的无向完全图有{n(n-1)}/2条边。
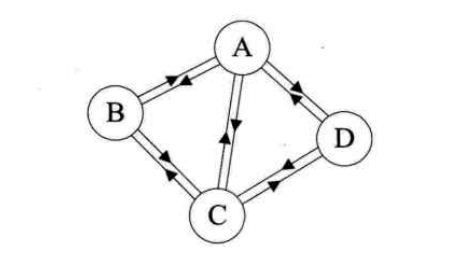
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。如图所示:含有n个顶点的有向完全图有n*(n-1)条边。
有很少条边或弧的图称为稀疏图,反之为稠密图。
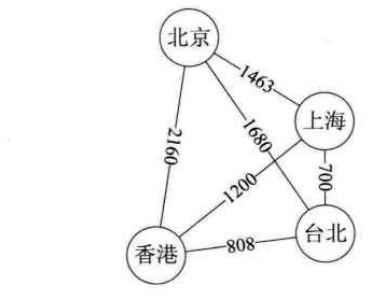
有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网。如图所示:
1.2图的顶点与边定义
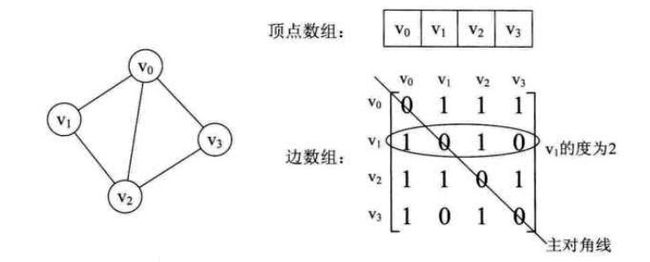
对于无向图G=(V,{E}),如果边(V,V’)属于E,则称顶点v和v'互为邻接点,即v和v'相邻接。边(v,v')依附于顶点v和v',或者说(v,v')与顶点v和v'相关联。顶点v的度是和v相关联的边的数目,记为TD(v)。如图所示:顶点A和B互为邻接点。
边数其实就是各顶点度数和的一半。
对于有向图G=(V,{E}),如果弧
树中根结点到任意结点的路径是唯一的,但是图中顶点与顶点之间的路径确是不唯一的。路径的长度是路径上的边或者弧的数目。
1.3连通图
在无向图G中,如果从顶点v到顶点v'有路径,则称v和v'是连通的。如果对于图中任意两个顶点vi、vj属于V,vi和vj都是连通的,则称G是连通图。如图所示:
二、图的存储结构
2.1邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
示例如下,下图是一个无向图:
顶点数组为vertex[4]={v0,v1,v2,v3},边数组arc[4][4]为上图右边这样的一个矩阵。无向图的边数组是一个对称矩阵。
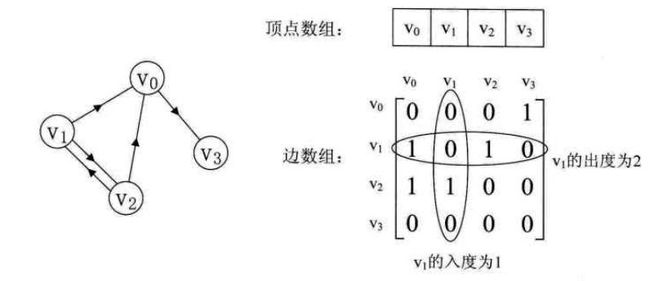
有向图示例如下:
有向图讲究出度和入度,v1的出度是行之和,v1的入度是列之和。
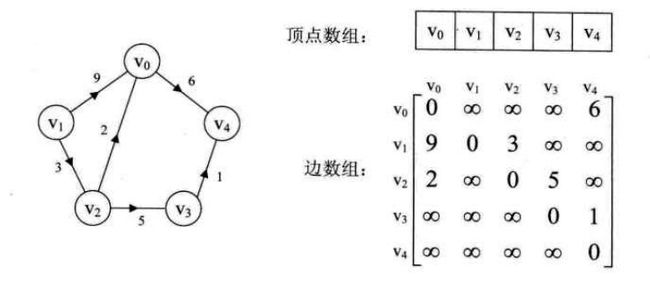
有向网图示例如下:
无穷表示一个计算机允许的、大于所有边上权值的值,也就是一个不可能的极限值。
2.2邻接表
邻接矩阵是一个不错的存储结构,对于边数相对顶点较少的图,这种结构是存在对存储空间的极大浪费的。
数组与链表相结合的存储方法称为邻接表。邻接表是这样的:
(1)图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过数组可以较容易的读取顶点信息,更加方便。另外,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
(2)图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
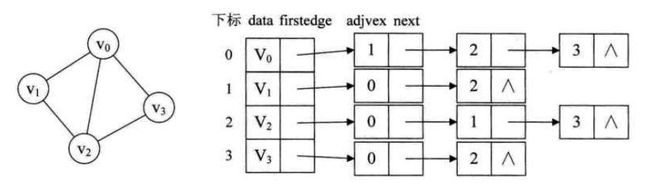
无向图的邻接表结构如下:
顶点的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
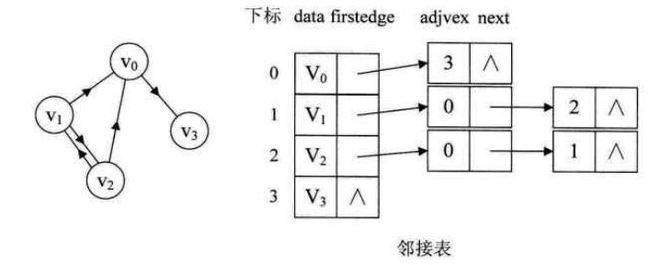
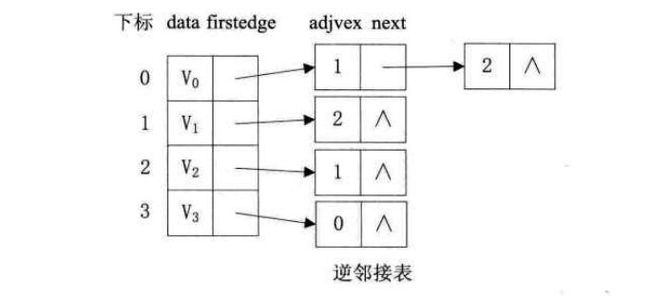
有向图的邻接表结构如下,但要注意的是有向图由于有方向,我们是以顶点为弧尾来存储边表的,这样和容易得到每个顶点的出度。但有时为了便于确定顶点的入度或以顶点为弧头的弧,我们可以建立一个有向图的逆邻接表,即对每个顶点vi都建立一个链接为vi为弧头的表。
2.3十字链表(有向图的邻接表改进)
对于有向图来说,邻接表是有缺陷的。关心了出度问题,想了解入度就必须要遍历整个图才能知道,反之,逆邻接表解决了入度确不了解出度的情况。把邻接表与逆邻接表结合起来,就是有向图的另一种存储方式:十字链表。顶点表结点结构如图所示:
其中firstin表示入边表头指针,指向该顶点的入边表中第一个结点,firstout表示出边表头指针,指向该顶点的出边表中的第一个结点。
边表结点结构如图所示:
其中tailvex是指弧起点在顶点表的下标,headvex是指弧终点在顶点表中的下标,headlink是指入边表指针域,指向终点相同的下一条边,taillink是指边表指针域,指向起点相同的下一条边。如果是网,还可以再增加一个weight域来存储权值。
2.4邻接多重表(无向图的邻接表改进)
如果我们在无向图的应用中,关注的重点是顶点,那么邻接表是不错的选择,但如果我们更关注边的操作,比如对已经访问过的边做标记,删除某一条边等操作,那就意味着,需要找到这条边的两个边表结点进行操作,这其实比较麻烦。
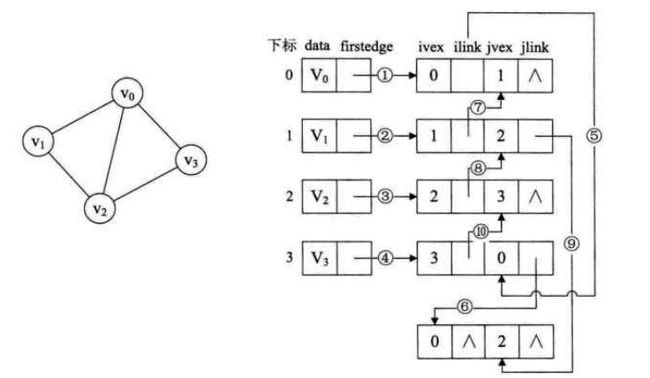
重新定义的边表结点结构如图所示:
ivex和jvex是与某条边依附的两个顶点在顶点表中的下标。ilink指向依附顶点ivex的下一条边,jlink指向依附顶点jvex的下一条边。这就是邻接多重表结构。
2.5边集数组
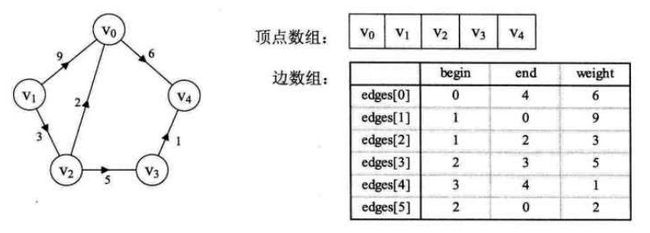
边集数组是由两个一维数组构成。一个是存储顶点的信息;另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成,如图所示:
显然边集数组关注的是边的集合,在边集数组中要查找一个顶点的度需要扫描整个边数组,效率并不高。因此它更适合对边依次进行处理的操作,而不适合对顶点相关的操作。
三、图的遍历
从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历。
3.1深度优先遍历(类似树的前序遍历)
深度优先遍历,也叫作深度优先搜索,简称DFS。
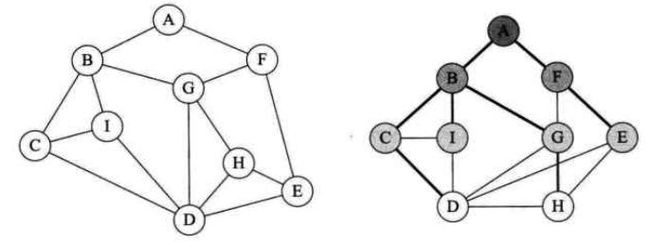
首先从顶点A开始,做上走过的标记后,前面有两条路,通向B和F,我们自己设定一个规则,在没有碰到重复顶点的情况下,始终是向右手边走,于是走到了B顶点。整个行路过程如上图所示。此时发现有三条分支,分别通向顶点C、I、G,右手通行原则,使得我们走到了C顶点。就这样,一直顺着右手通道走,一直走到F顶点。当依然选择右手通道走过去后,发现走回到顶点A,而此时顶点A做了走过的标记,因此退回到顶点F,走向从右数的第二条通道,到了G顶点,它有三条通道,发现B和D都已经是走过的,于是走到了H,当面对通向H的两条通道D和E时,会发现都已经走过了。
此时是否已经遍历了所有顶点?没有。可能还有很多分支的顶点我们没有走到,所以按原路返回。在顶点H处,再无通道没走过,返回到G,也无未走过通道,返回F,没有通道,返回到E,有一条通道通往H的通道,验证后也是走过的,再返回到顶点D,此时H走过了,G走过了,I未走过,赶快记下来。继续返回,直到返回顶点A,确认已经完成遍历任务,找到了所有的9个顶点。
深度优先遍历其实就是一个递归的过程。它从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。
3.2广度优先遍历(类似树的层序遍历)
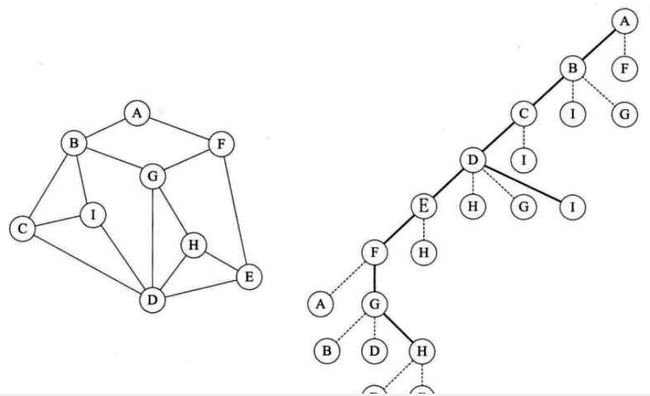
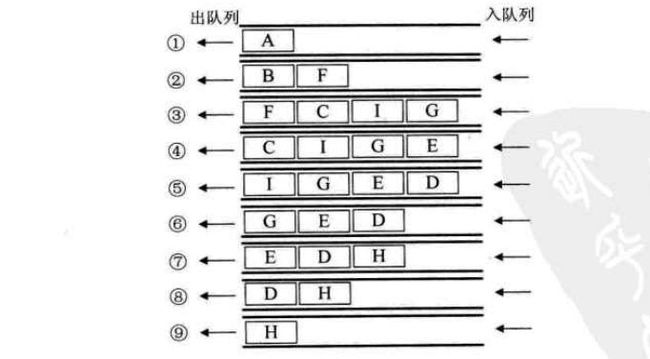
广度优先遍历,又称为广度优先搜索,简称BFS。
对上图进行变形,变形原则是顶点A放置在最上第一层,让与它有边的顶点B、F为第二层,再让与B和F有边的顶点C、I、G、E为第三层,再将这四个顶点有边的D、H放在第四层,如图所示。