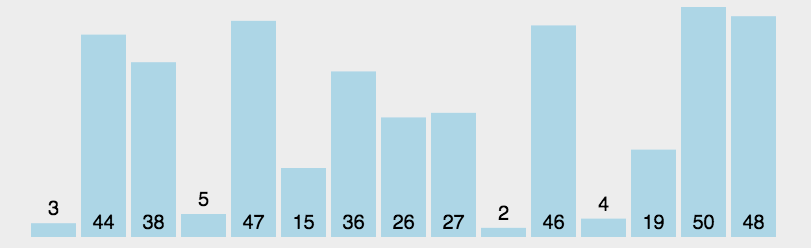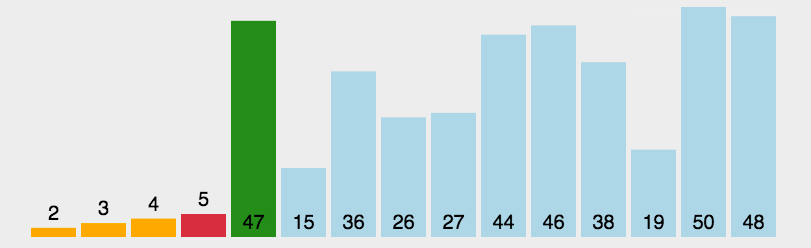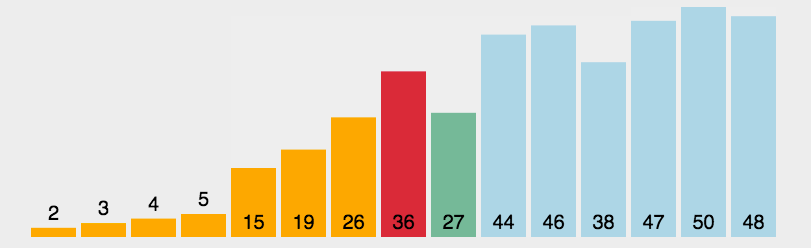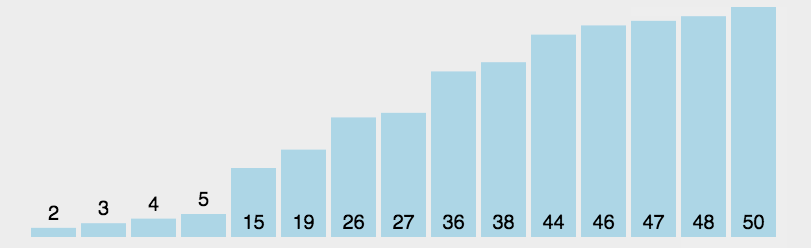
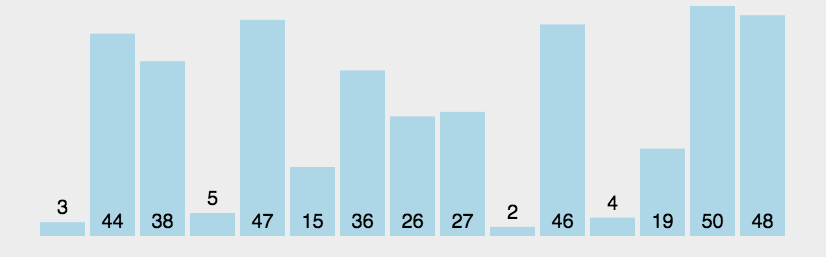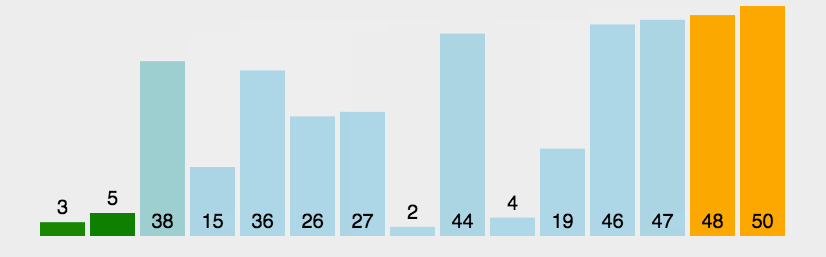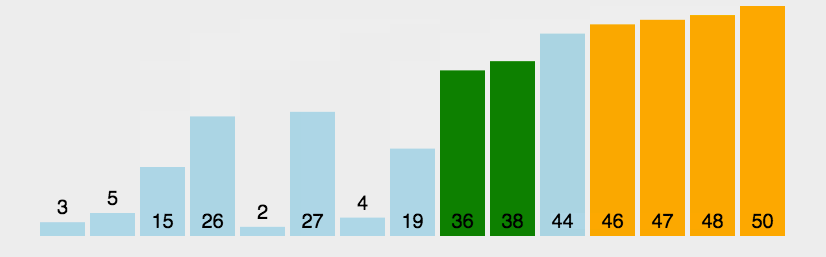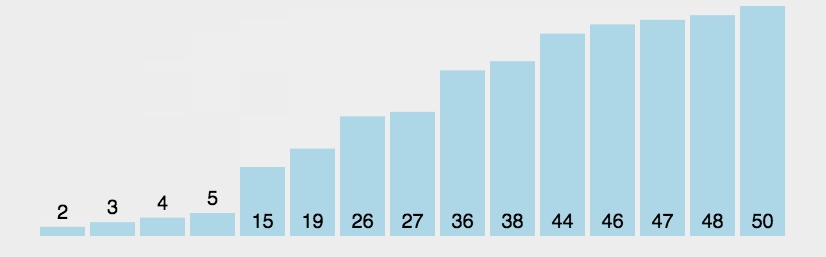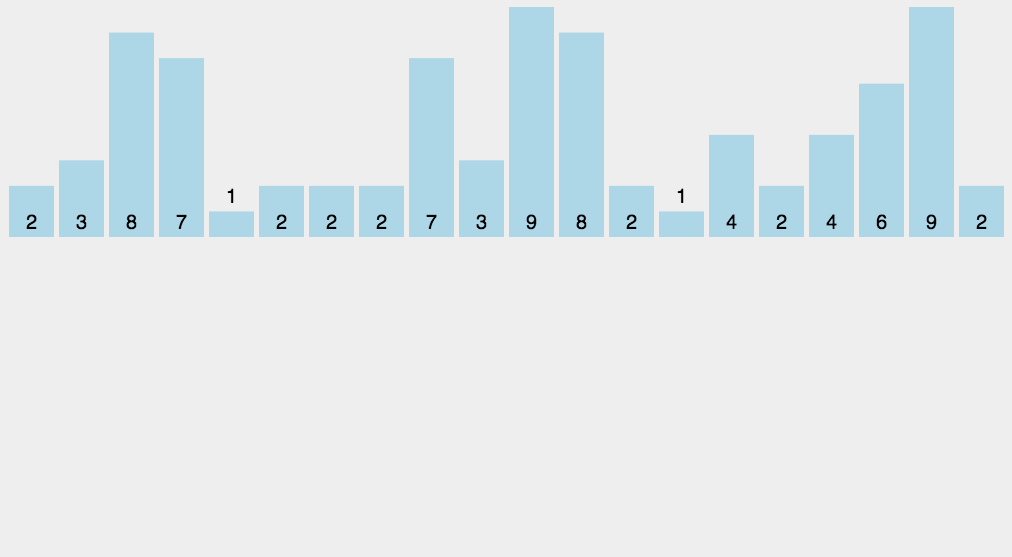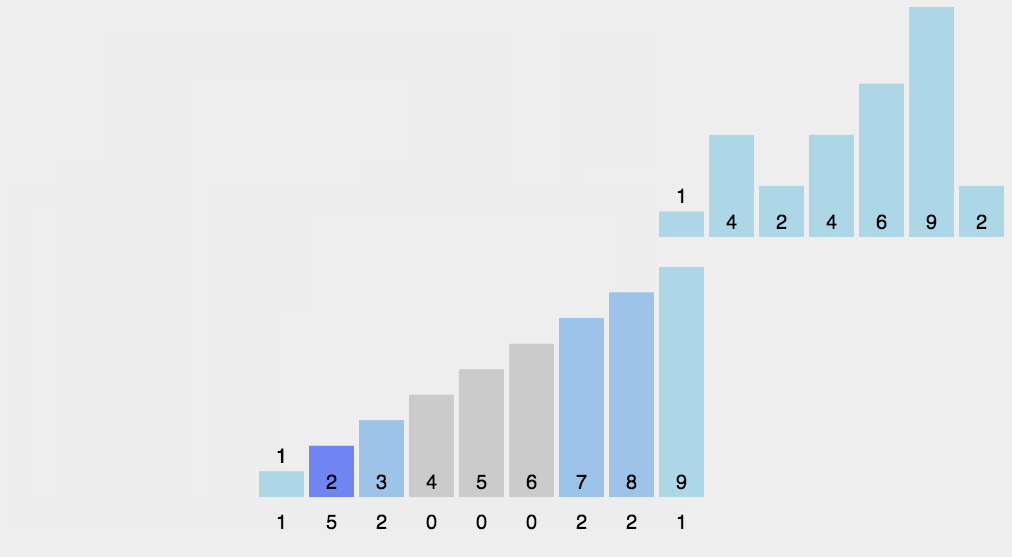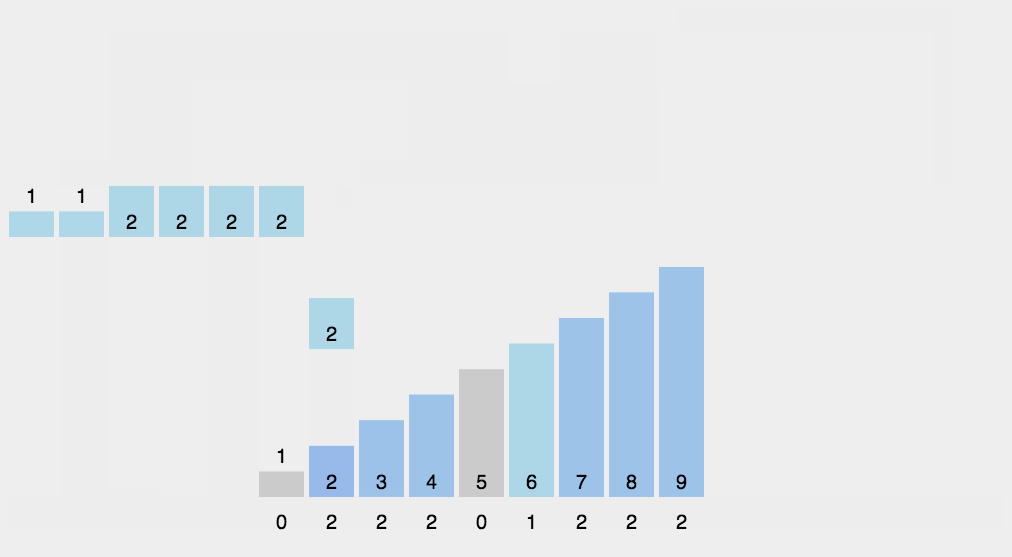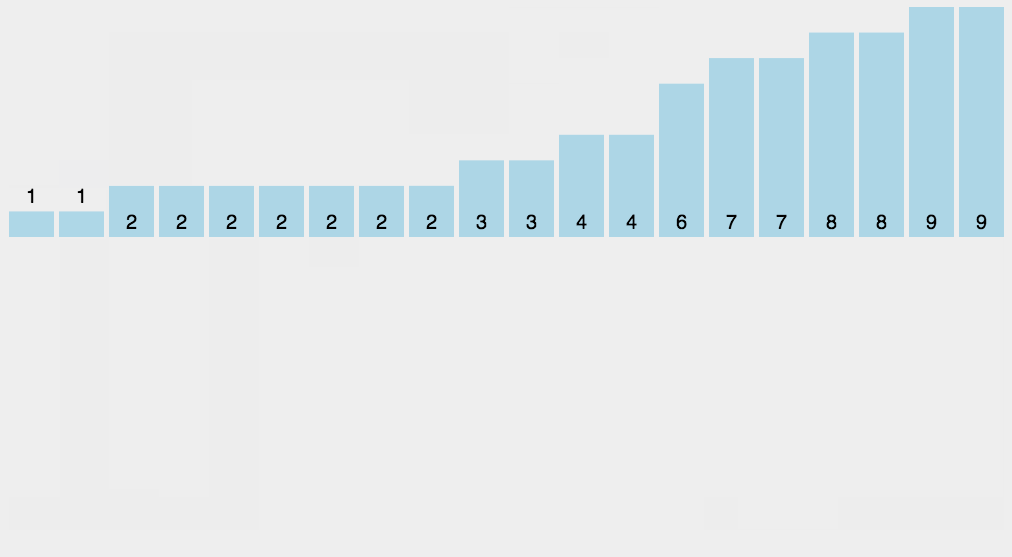数据结构与算法(一)——十大常见排序算法
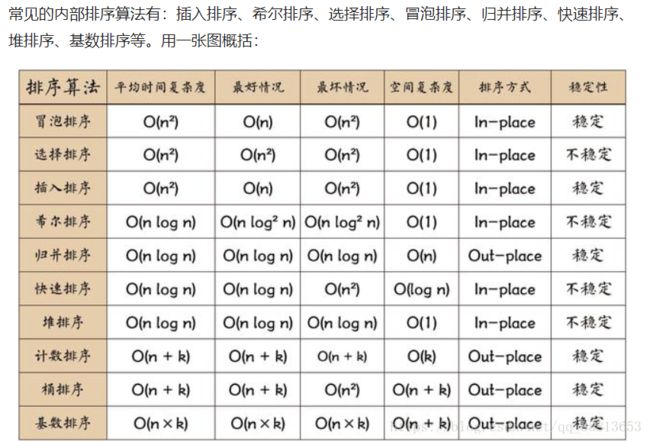
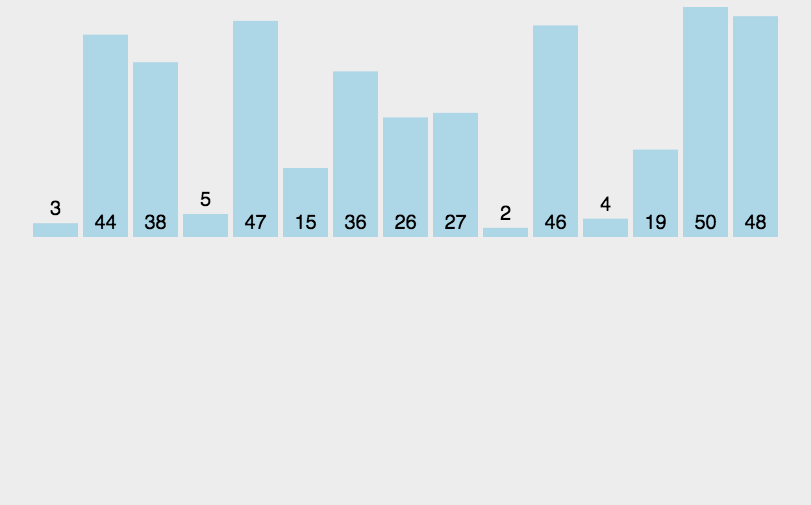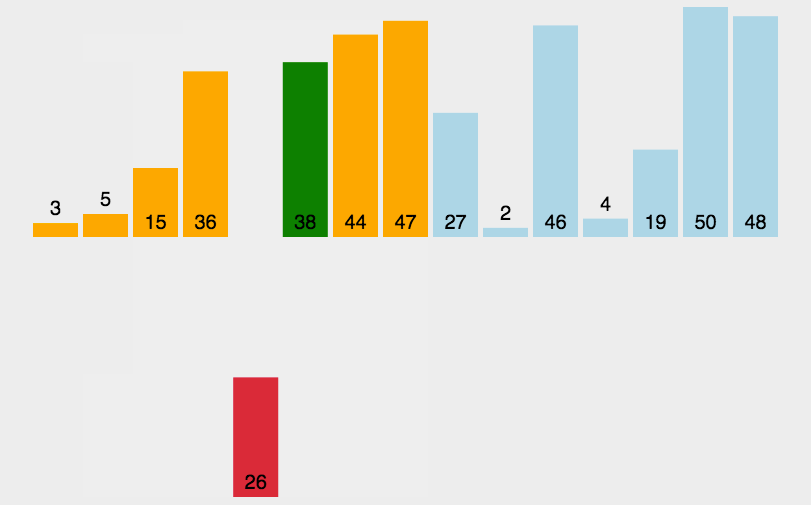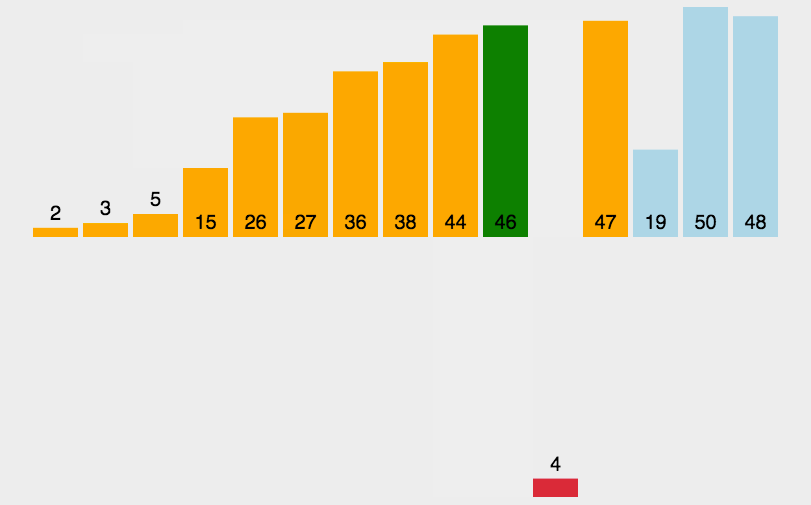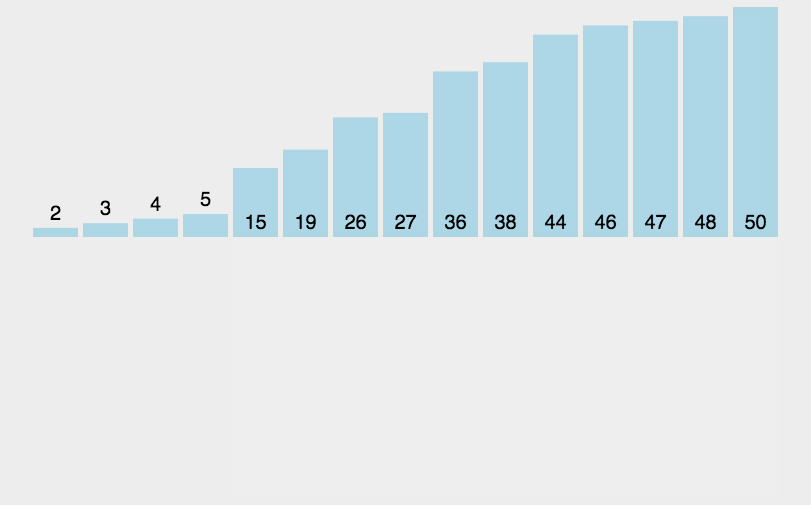
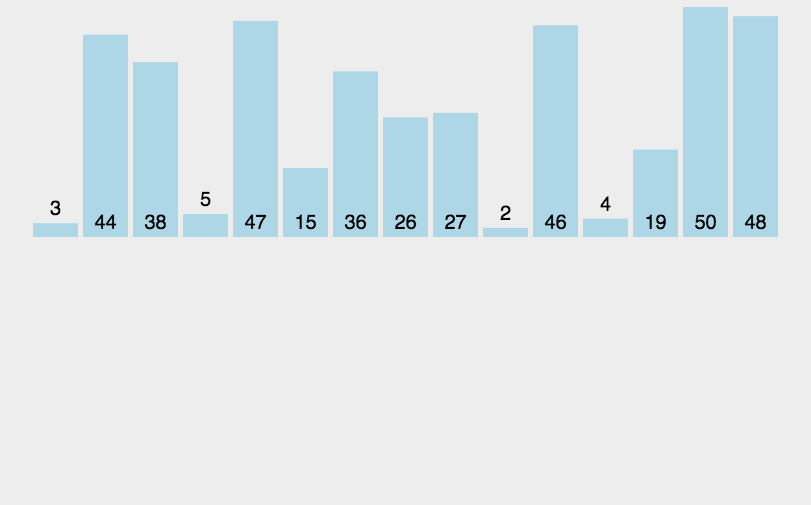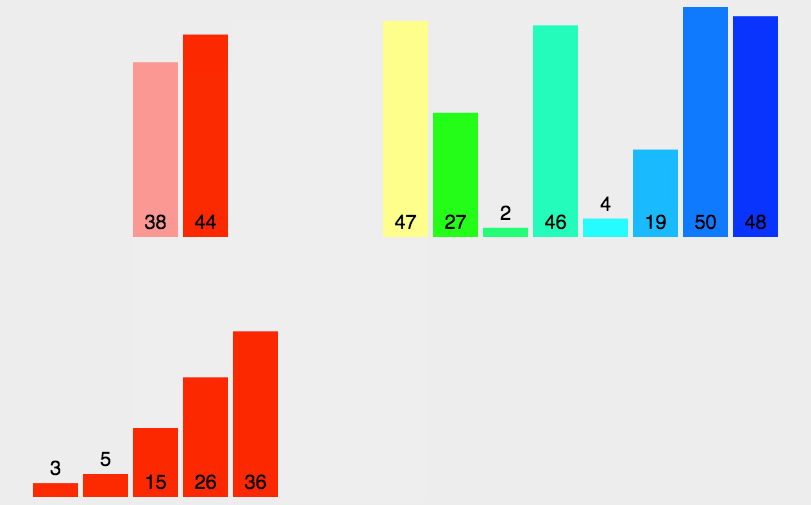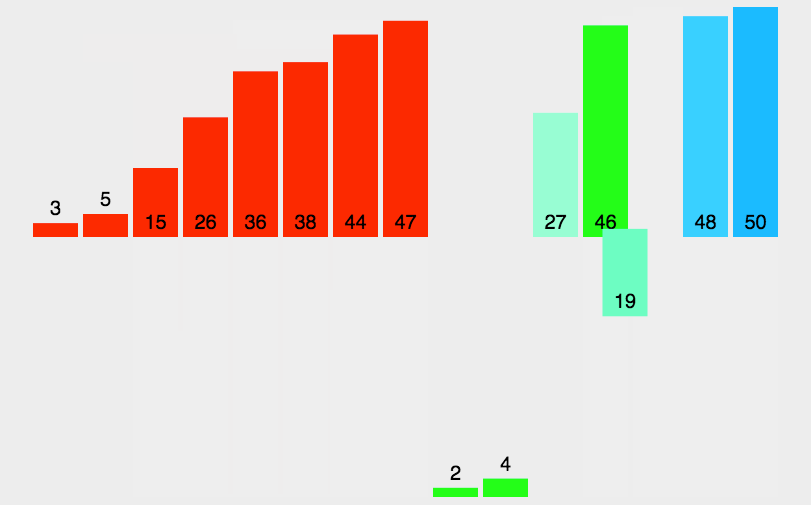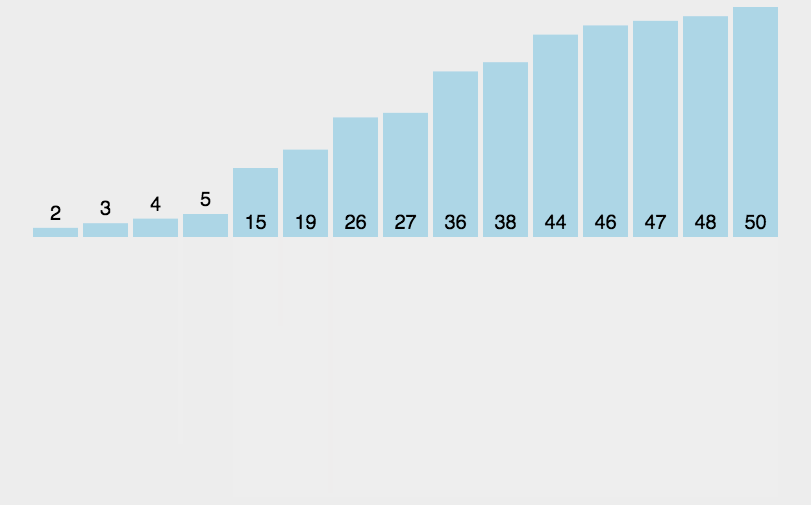
一、排序算法概述
**排序算法最常用操作:交换元素
/**
* 交换数组内两个元素
*
* @param array
* @param i
* @param j
*/
private void swap(T[] array, int i, int j) {
//临时变量记录即将改变的元素
T temp = array[i];
array[i] = array[j];
array[j] = temp;
}二、冒泡排序
2.1 实现原理
第一种:元素上浮,从右(大)往左(小)依次确认,相邻元素间,如果右小于左,则交换,每次确认一位最小数。
第二种:元素下沉,从左(小)往右(大)依次确认,相邻元素间,如果左大于右,则交换,每次确认一位最大数。
2.2 动图解析
2.3 代码实现
/**
* 冒泡排序(从大到小开始确定:从左往右,大的元素向右交换)
*
* @param arr 按照元素hash值排序
* @return
*/
private T[] sortByBubbling(T[] arr) {
//排除空异常
if (arr == null || arr.length == 0) {
return arr;
}
//从末尾元素开始确定
for (int i = arr.length - 1; i > 0; i--) {
//判断是否存在交换
boolean flag = false;
for (int j = 0; j < i; j++) {
if (arr[j].hashCode() > arr[j + 1].hashCode()) {
swap(arr, j, j + 1);
flag = true;
}
}
//如果不再存在交换,则排序完毕,直接退出
if (!flag) {
break;
}
}
return arr;
}三、选择排序
3.1 实现原理
第一种:拿未确认的最左位元素,依次和右边元素比较,如果右边元素更小,则交换
第二种:拿未确认的最右位元素,依次和左边元素比较,如果左边元素更大,则交换
3.2 动图解析
3.3 代码实现
/**
* 选择排序(从最左开始,依次和右边比较,如果大于则交换)
*
* @param arr
* @return
*/
private T[] sortBySelect(T[] arr) {
//排除空异常
if (arr == null || arr.length == 0) {
return arr;
}
//从第一位元素开始确定
for (int i = 0; i < arr.length - 1; i++) {
//记录当前获得最小值的索引(取代实际交换操作)
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j].hashCode() < arr[min].hashCode()) {
min = j;
}
}
swap(arr, i, min);
}
return arr;
}四、插入排序
4.1 实现原理
将某一元素插入已经排序好的数组中,
第一种:元素位于数组右方,则元素依次与左方比较,找出合适位置,被比较元素后移一位,该元素前置
第二种:元素位于数组左方,则元素依次与右方比较,找出合适位置,被比较元素前移一位,该元素后置
4.2 动图解析
4.3 代码实现
/**
* 插入排序(将一个元素与已经排序好的数组元素依次比较,可从右开始比较:如果小于则插入元素左移)
*
* @param arr
* @return
*/
private T[] sortByInsert(T[] arr) {
//排除空异常
if (arr == null || arr.length == 0) {
return arr;
}
//从第二位开始,比较元素前面的元素为排序好的数组
for (int i = 1; i < arr.length; i++) {
T temp = arr[i];
//定义被比较数组元素所在位
int j = i - 1;
while (j >= 0 && temp.hashCode() < arr[j].hashCode()) {
arr[j + 1] = arr[j];
j--;
}
//将插入元素前置
arr[j + 1] = temp;
}
return arr;
}五、希尔排序
5.1 实现原理
按照一定间隔(记d)执行插入排序
第一种:元素位于数组右方,记索引为x,则元素依次与左方x-d的元素比较,找出合适位置,被比较元素后移一位,该元素前置
第二种:元素位于数组左方,记索引为x,则元素依次与右方x+d的元素比较,找出合适位置,被比较元素前移一位,该元素后置
5.2 动态解析
5.3 代码实现
/**
* 希尔排序(类似于插入排序,不过希尔是按照一定间隔插入)
*
* @param arr
* @return
*/
private T[] sortByShell(T[] arr) {
//排除空异常
if (arr == null || arr.length == 0) {
return arr;
}
//假定初始间隔为数组长度二分之一,每次再乘以二分之一
int len = arr.length / 2;
while (len != 0) {
for (int i = len; i < arr.length; i++) {
T temp = arr[i];
//获取与比较元素间隔len长度的数组元素
int j = i - len;
//插入排序
while (j >= 0 && (temp.hashCode() < arr[j].hashCode())) {
arr[j + len] = arr[j];
j = j - len;
}
arr[len + j] = temp;
}
len = len / 2;
}
return arr;
}六、归并(合并)排序
6.1 实现原理
采用分而治之的思想:
将数组等分为若干子数组,对每个子数组排序,然后再合并有序的子数组
6.2 动态解析
6.3 代码实现
/**
* 归并排序
*
* @param array
* @return
*/
public int[] sortByMerge(int[] array) {
//排除空异常
if (array == null || array.length < 2) {
return array;
}
int mid = array.length / 2;
int[] left = Arrays.copyOfRange(array, 0, mid);
int[] right = Arrays.copyOfRange(array, mid, array.length);
//调用栈
return merge(sortByMerge(left), sortByMerge(right));
}
/**
* 归并排序——将两段排序好的数组结合成一个排序数组
*
* @param left
* @param right
* @return
*/
public int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
for (int index = 0, i = 0, j = 0; index < result.length; index++) {
//如果一方数组元素已经排完,则只排入另一方数组元素
if (i >= left.length) {
result[index] = right[j++];
} else if (j >= right.length) {
result[index] = left[i++];
} else if (left[i] > right[j]) {
//将两个数组中从小到大合并
result[index] = right[j++];
} else {
result[index] = left[i++];
}
}
return result;
}七、快速排序
7.1 实现原理
采用分而治之的思想:
第一步、选取基准值,小于基准值的在左侧作为子数组,大于基准值的在右侧作为子数组,
第二步、再对两个子数组重复上一步操作
第三步、合并所有子数组
7.2 动图解析
7.3 代码实现
/**
* 快速排序——分而治之思想,将问题最小线性化
*
* @param array
* @param start
* @param end
* @return
*/
public T[] sortByQuick(T[] array, int start, int end) {
//排除无效参数
if (array == null || array.length == 0 || start < 0 || end >= array.length || start > end) {
return array;
}
//一次快排后小于基准值的最大索引
int smallIndex = partition(array, start, end);
//快排小于基准值的子数组
if (smallIndex > start) {
sortByQuick(array, start, smallIndex - 1);
}
//快排大于基准值的子数组
if (smallIndex < end) {
sortByQuick(array, smallIndex + 1, end);
}
return array;
}
/**
* 快速排序算法——partition
*
* @param array
* @param start
* @param end
* @return
*/
public int partition(T[] array, int start, int end) {
//随机寻找基准值所在位
int pivot = start + (end - start)/2;
//小于基准值的元素应在的索引位置
int smallIndex = start - 1;
//将基准值放在最右侧
swap(array, pivot, end);
for (int i = start; i <= end; i++)
//小于等于基准值的放在基准值左侧
if (array[i].hashCode() <= array[end].hashCode()) {
smallIndex++;
if (i > smallIndex) {
swap(array, i, smallIndex);
}
}
return smallIndex;
}八、堆排序
8.1 实现原理
将待排序序列构造成一个大顶堆(arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] ),此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
8.2 动图解析
8.3 代码实现
/**
* 堆排序
*
* @param array
* @return
*/
public T[] sortByHeap(T[] array) {
int len;
if (array == null || (len = array.length) < 2) {
return null;
}
//1.构建一个最大堆
buildMaxHeap(array, len);
//2.循环将堆首位(最大值)与末位交换,然后在重新调整最大堆
while (len > 0) {
swap(array, 0, len - 1);
len--;
adjustHeap(array, 0, len);
}
return array;
}
/**
* 建立最大堆
*
* @param array
* @param len 未确认元素个数
*/
public void buildMaxHeap(T[] array, int len) {
//从最后一个非叶子节点开始向上构造最大堆
for (int i = (len / 2 - 1); i >= 0; i--) {
adjustHeap(array, i, len);
}
}
/**
* 调整使之成为最大堆
*
* @param array
* @param i 堆顶索引
* @param len
*/
public void adjustHeap(T[] array, int i, int len) {
int maxIndex = i;
//如果有左子树,且左子树大于父节点,则将最大指针指向左子树
if (i * 2 < len && array[i * 2].hashCode() > array[maxIndex].hashCode()) {
maxIndex = i * 2;
}
//如果有右子树,且右子树大于父节点,则将最大指针指向右子树
if (i * 2 + 1 < len && array[i * 2 + 1].hashCode() > array[maxIndex].hashCode()) {
maxIndex = i * 2 + 1;
}
//如果父节点不是最大值,则将父节点与最大值交换,并且递归调整与父节点交换的位置。
if (maxIndex != i) {
swap(array, maxIndex, i);
adjustHeap(array, maxIndex, len);
}
}九、计数排序
9.1 实现原理
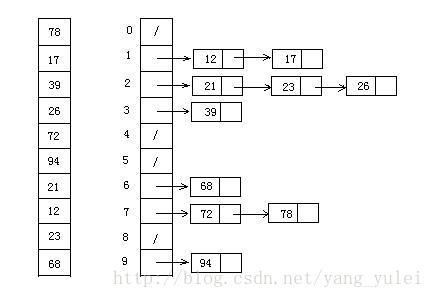
利用桶的概念:一个桶存单一的键值
根据待排序数组A创建计数数组B,B首位代表A最小值,B末位代表A最大值,遍历A,在B中记录所有元素出现次数。遍历B,根据索引与最小值距离,以及出现次数排序。
9.2 动图解析
9.3 代码实现
/**
* 计数排序(获取数组中的最大值和最小值,建立从最小值到最大值的计数数组,遍历原来的数组,将元素出现次数记录在计数数组中)
*
* @param array
* @return
*/
public int[] sortByCount(int[] array) {
//干扰排除
if (array == null || array.length < 2) {
return array;
}
//获取数组最大值和最小值
int bias, min = array[0], max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
bias = 0 - min;
//创建计数数组
int[] bucket = new int[max - min + 1];
for (int i = 0; i < array.length; i++) {
//记录待排序数组元素(距离最小值长度就是在计数数组中的索引值)出现次数
bucket[array[i] + bias]++;
}
int index = 0, i = 0;
while (index < array.length) {
if (bucket[i] != 0) {
array[index] = i - bias;
bucket[i]--;
index++;
} else {
i++;
}
}
return array;
}十、桶排序
10.1 实现原理
利用桶的概念:一个桶存一定范围的元素
设置一个定量的数组当作空桶,遍历输入数据,并且把数据一个一个放到对应的桶里去,对每个不是空的桶进行排序,从不是空的桶里把排好序的数据拼接起来。
10.2 图形解析
10.3 代码实现
/**
* 桶排序
*
* @param array
* @param bucketSize
* @return
*/
public ArrayList sortByBucket(ArrayList array, int bucketSize) {
if (array == null || array.size() < 2) {
return array;
}
T max = array.get(0), min = array.get(0);
// 找到最大值最小值
for (T anArray1 : array) {
if (anArray1.hashCode() > max.hashCode()) {
max = anArray1;
}
if (anArray1.hashCode() < min.hashCode()) {
min = anArray1;
}
}
//桶数目
int bucketCount = (max.hashCode() - min.hashCode()) / bucketSize + 1;
ArrayList> bucketArr = new ArrayList<>(bucketCount);
ArrayList resultArr = new ArrayList<>();
for (int i = 0; i < bucketCount; i++) {
bucketArr.add(new ArrayList<>());
}
for (T anArray : array) {
bucketArr.get((anArray.hashCode() - min.hashCode()) / bucketSize).add(anArray);
}
for (int i = 0; i < bucketCount; i++) {
if (bucketSize == 1) {
resultArr.addAll(bucketArr.get(i));
} else {
if (bucketCount == 1)
bucketSize--;
ArrayList temp = sortByBucket(bucketArr.get(i), bucketSize);
resultArr.addAll(temp);
}
}
return resultArr;
} 十一、基数排序
11.1 实现原理
利用桶的概念:根据键值的每位数字来分配桶
取得数组中的最大数,并取得位数;
arr为原始数组,从最低位开始取每个位组成radix数组;
对radix进行计数排序(利用计数排序适用于小范围数的特点);
11.2 动图解析
11.3 代码实现
/**
* 基数排序
*
* @return
* @paramarray
*/
public int[] sortByRadix(int[] array) {
if (array == null || array.length < 2) {
return array;
}
// 1.先算出最大数的位数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
max = Math.max(max, array[i]);
}
int maxDigit = String.valueOf(max).length();
//求目标位上的数字
int mod = 10, div = 1;
ArrayList> bucketList = new ArrayList<>();
for (int i = 0; i < 10; i++) {
bucketList.add(new ArrayList<>());
}
for (int i = 0; i < maxDigit; i++, mod *= 10, div *= 10) {
for (int anArray : array) {
int num = (anArray % mod) / div;
bucketList.get(num).add(anArray);
}
int index = 0;
for (ArrayList aBucketList : bucketList) {
for (Integer anABucketList : aBucketList) {
array[index++] = anABucketList;
}
aBucketList.clear();
}
}
return array;
} 十二、运行测试
12.1 测试代码
public static void main(String[] args) {
//获取目标对象与参数
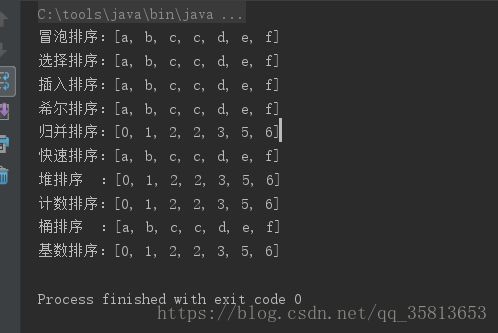
SortWay12.2 测试结果
12.3 代码链接
https://download.csdn.net/download/qq_35813653/10723872